ОСНОВНЫЕ ПРАВИЛА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
При производстве вычислений получающиеся числа приходится округлять. Округление заключается в замене исходного числа другим числом с меньшим количеством цифр. Если первая из отбрасываемых цифр равна или больше пяти, то последняя цифра оставшегося числа увеличивается на единицу. Если отбрасываемая часть состоит только из одной цифры «пять», то последняя остающаяся цифра сохраняется неизменной, если она четная, и увеличивается на единицу, если она нечетная (правило четной цифры).
Все отличные от нуля цифры в изображении числа называются значащими. Нуль является значащим, если он стоит в середине или в конце числа. Первые нули в десятичных дробях значащими не являются.
Примеры:
0,2307 – четыре значащих цифры;
0,00052 – две значащих цифры;
10520 – пять значащих цифр;
3,28 – три значащих цифры;
3,280 – четыре значащих цифры.
При написании больших и очень малых чисел рекомендуется пользоваться степенью десяти (опыт показывает, что пренебрежение этой рекомендацией часто приводит к ошибкам при чтении и записи чисел):
23756,82 = 2,38×104;
0,000175621 = 1,76×10–4 = 17,6×10–5.
Оба числа округлены до третьей значащей цифры.
Количество значащих цифр при такой форме записи определяется, во-первых, требуемой точностью, а во-вторых, зависит от количества верных цифр в исходном числе. Если, например, известно, что в числе a = 26352300 сомнительна пятая цифра, то ясно, что больше четырех цифр брать нет смысла, и это число можно представить так: a = 2,635×107 .
|
|
|
При оценке точности получаемых результатов пользуются понятиями абсолютной и относительной погрешностей.
Абсолютной погрешностью называется модуль разности между точным числом A и его приближенным значением a:
D = ú A – a ú.
При правильном округлении абсолютная погрешность не превышает пяти единиц разряда, следующего за последней оставляемой цифрой. Например, число a = 8,237 могло получиться в результате округления как числа 8,23651, так и числа 8,23749. Как в том, так и в другом случае мы добавляем или отбрасываем не более, чем 0,0005. Поэтому мы пишем, что здесь абсолютная погрешность не превышает пяти десятичных:
D £ Da,
где Da = 0,0005.
Величина Da, стоящая справа от знака неравенства и ограничивающая величину абсолютной погрешности, представляет собой так называемую предельную абсолютную погрешность, определяющую максимально возможное значение абсолютной погрешности при данных конкретных обстоятельствах (величине числа и количестве оставляемых при округлении цифр).
По имеющемуся приближенному числу a можно определить границы, в которых лежит его точное значение A.
Так как D = ú A – a ú и ú A – a ú £ Da, то – Da £ A – a £ Da.
|
|
|
Отсюда a - Da £ A £ a + Da.
Пусть, например, a = 3,16. Для него Da = 0,005 (пять единиц разряда, следующего за его последней цифрой). Поэтому a – Da = 3,155, a + Da = 3,165, и точное значение числа A лежит в пределах:
3,155 £ A £ 3,165.
Из последнего двойного неравенства видно, что число 3,16 могло получиться при округлении любого из чисел, лежащих в указанных границах.
По величине абсолютной погрешности невозможно судить о точности числа. Пусть, например, абсолютная погрешность вычисления или измерения тока равна 0,2 ампера. Много это или мало?
Если действительное значение тока довольно велико, например, 175 A, а мы получили 174,8 A, то это хороший результат. Если же точное значение 0,1 A, а мы получили 0,3 A, то ясно, что этот результат никуда не годится.
Мерой точности приближенного числа может служить только относительная погрешность, равная отношению абсолютной погрешности к модулю точного значения числа:
d =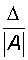 
.
Так как на практике A » a, то обычно принимают
d @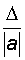 
.
Как и у абсолютной погрешности, существует предельное значение da и у относительной погрешности d:
d £ da.
Ее величина da =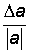 
или в процентах: da % = 
.
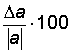Для упомянутого ранее числа 8,237:
da % =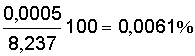 
.
|
|
|
Полученный результат говорит о том, что относительная погрешность приближенного числа 8,237 (возникшая при округлении) не превышает 0,0061 %.
Выше были записаны два числа:
a1 = 3,28 и a2 = 3,280.
На первый взгляд эти числа совершенно одинаковы. Однако это не так. Их предельные абсолютные и относительные погрешности соответственно равны:
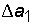= 0,005, δa1% = 
;
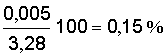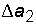= 0,0005, δa2% = 
.
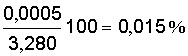То есть второе число является более точным.
Ясно, что величина относительной погрешности, возникающей при округлении, зависит от того, какое количество значащих цифр содержит число. Нетрудно показать, что если после округления число имеет n значащих цифр, а a – его первая цифра, то предельная относительная погрешность (в процентах) может определяться по формуле:
da % =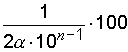 
.
При оценке величины относительной погрешности наиболее неблагоприятной является ситуация, когда первая цифра числа равна единице.
В этом случае предельная относительная погрешность при заданном числе значащих цифр имеет наибольшее значение, равное
da max % =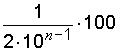 
.
Для наглядности максимальные значения предельной относительной погрешности, вычисленные по последней формуле, приведены в таблице приложения.
Эта таблица позволяет определить нужное количество цифр в числе для достижения требуемой точности.
|
|
|
Если, например, относительная погрешность числа не должна превышать 0,05 %, то при округлении следует сохранять четыре значащих цифры.
Таблица П.1
Максимальные значения предельной относительной погрешности
| Количество значащих цифр числа | 1 | 2 | 3 | 4 | 5 | 6 |
| da max,% | 50 | 5 | 0,5 | 0,05 | 0,005 | 0,0005 |
При выполнении арифметических операций всегда возникает вопрос, сколько значащих цифр и десятичных знаков должен содержать результат.
Производя вычисления на микрокалькуляторе, студенты часто выписывают с индикатора все имеющиеся цифры. Это занятие совершенно бессмысленно. Во-первых, работа с большим количеством цифр является источником дополнительных ошибок, а во-вторых, при выполнении учебных заданий не требуется проводить вычисления с такой высокой точностью. Обычно хватает 3–4 значащих цифр.
Чтобы избежать этой ненужной работы и в то же время получить необходимую точность, при выполнении расчетов рекомендуется руководствоваться данными, приведенными в таблице приложения, и следующими правилами.
1. При производстве вычислений во всех промежуточных выкладках следует брать на одну цифру больше, чем требуется в окончательном результате. То есть, если итог вычислений необходимо получить с тремя значащими цифрами, то расчеты следует вести по четырем цифрам.
В окончательном результате «запасная» цифра отбрасывается.
2. При сложении и вычитании в получаемом результате следует сохранять столько десятичных знаков, сколько их в слагаемом, содержащем наименьшее число десятичных знаков. Предварительно все слагаемые, содержащие большее число десятичных знаков, необходимо округлить, сохраняя одну лишнюю цифру. Например:
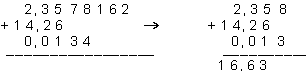
3. При умножении и делении результат должен содержать столько значащих цифр, сколько их в сомножителе с наименьшим числом значащих цифр. Предварительно все сомножители, содержащие большее число значащих цифр, следует округлить, сохраняя одну лишнюю значащую цифру:
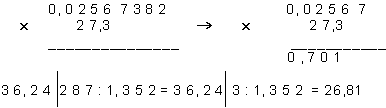
4. При возведении числа в квадрат или куб и при извлечении корня (квадратного, кубического) в получаемом результате следует писать столько значащих цифр, сколько их содержит исходное число:
; 
.
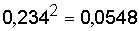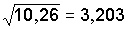И в заключение – правило оформления расчетов.
Когда мы проводим вычисления по какому-либо выражению, то оформляем их следующим образом: записываем расчетную формулу, после знака равенства показываем подстановку числовых значений и, наконец, пишем результат и единицу измерения. Например:
= 
.
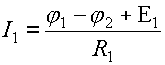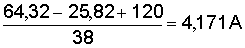БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Основы теории цепей: Учеб. для вузов / Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.
2. Теоретические основы электротехники: Учеб. для вузов / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чепурин. В 2 т. – 4-е изд. – СПб.: Питер, 2003. – Т. 1. – 463 с.
3. Попов, В.П. Основы теории цепей: Учеб. для вузов / В.П. Попов. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1998. – 575 с.
4. Нейман, Л.Р. Теоретические основы электротехники: Учеб. для вузов / Л.Р. Нейман, К.С. Демирчян. – 4-е изд. – Л.: Энергия, 1981. – Т. 1. – 536 с.
5. Шебес, М.Р. Задачник по теории линейных электрических цепей: Учеб. пособие / М.Р. Шебес, М.В. Каблукова. – 4-е изд., перераб. и доп. – М.: Высшая школа, 1990. – 544 с.
6. Шебес, М.Р. Сборник упражнений и задач по теоретическим основам электротехники: Учеб. пособие / М.Р. Шебес. – М.: Высшая школа, 1962.
– 472 с.
7. Матющенко, В.С. Теоретические основы электротехники. Линейные электрические цепи постоянного и однофазного синусоидального токов: Учеб. пособие / В.С. Матющенко. – Хабаровск: Изд-во ДВГУПС, 2002. – 112 с.
Дата добавления: 2019-07-17; просмотров: 268; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!