Числовые значения параметров цепи синусоидального тока

Примечание. Частота ЭДС во всех вариантах составляет 50 Гц

ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ

Напоминаем, что комплексным числом называется выражение вида

где – мнимая единица.

Это – алгебраическая форма комплексного числа. На комплексной плоскости ему соответствует вектор , а составляющие и определяют его проекции на оси (рис. 10.1).

Так как

, (10.1)

, (10.2)

то, используя формулу Эйлера

получим так называемую показательную форму комплексного числа

При выполнении расчетов нам необходимы обе формы записи. Алгебраическая нужна для сложения и вычитания комплексных чисел, а также для выполнения проверок по законам Кирхгофа и балансу мощностей. Умножение и деление целесообразно выполнять в показательной форме. Последняя нужна еще и потому, что величины токов и напряжений определяются модулями соответствующих комплексных чисел.

Эти соображения требуют написания всех результатов в обеих формах.

Перевод из показательной формы в алгебраическую осуществляется по формулам (10.1) и (10.2). Обратный перевод можно выполнить с помощью выражений:

; (10.3)

или в другом порядке:

; (10.4)

При расчетах тригонометрических величин на микрокалькуляторе необходимо внимательно следить за получаемыми результатами.

Так, если мы имеем комплексное число и определяем его аргумент по формуле (10.4), то получаем

Для числа имеем

Получили тот же самый угол, хотя ясно, что аргументы этих комплексных чисел различны (рис. 10.2).

Рис. 10.2. Определение аргумента комплексного числа

Как видно из рисунка, аргумент второго комплексного числа найден неверно.

Если буквой обозначить угол, выдаваемый калькулятором, то в обоих случаях = –36,87°.

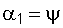Но , а .

Поэтому

; .

То есть аргумент комплексного числа мы определяем с помощью рисунка, найдя по проекциям вектора (по вещественной и мнимой составляющим комплексного числа) квадрант, в котором этот вектор находится.

Аналогичная ситуация получается, когда у комплексных чисел

мы по формулам (10.3) сначала определяем модуль

а затем аргумент

И в том, и в другом случае мы получаем один и тот же результат, хотя на самом деле аргументы этих комплексных чисел различны (рис. 10.3):

Рис. 10.3. Сопряженные комплексные числа

Напоминаем, что два комплексных числа, изображаемые на комплексной плоскости векторами, симметричными относительно вещественной оси, называются сопряжёнными.

На первом этапе вычислений в подобных затруднительных случаях рекомендуется рисовать вектор на комплексной плоскости и записывать комплексное число с помощью этого рисунка. В дальнейшем, по мере приобретения навыка, надобность в таких рисунках отпадёт.

Приведенные выше формулы можно использовать прямо в той последовательности, как они записаны. Однако это не всегда удобно. Например, при проведении вычислений на микрокалькуляторе по формулам (10.1) и (10.2) приходится дважды набирать на клавиатуре 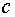и – один раз для определения , второй раз для отыскания .

Выпускаемые в настоящее время микрокалькуляторы имеют регистры памяти, что позволяет составить такую последовательность нажатия клавиш, при которой каждая составляющая комплексного числа набирается на клавиатуре только один раз. Хорошо изучив свой микрокалькулятор и инструкцию к нему, учащийся может сам разработать удобные для себя методы. При работе с программируемым микрокалькулятором имеется возможность сохранить программу в памяти машины. Как это делается, можно прочитать в руководстве по эксплуатации микрокалькулятора.

В любом случае выбранный метод вычислений нужно проверить с помощью контрольных задач.

Например:

Дата добавления: 2019-07-17; просмотров: 247; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!