ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ МЕЖДУ ДВУМЯ ТОЧКАМИ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Эта задача при расчете электрических цепей встречается очень часто. Пусть, например, в цепи на рис. 2.1 требуется найти напряжение между точками m и n.
Прежде всего необходимо показать на схеме или мысленно представить стрелку этого напряжения. Её направление определяется порядком следования индексов у буквы 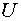 . Для напряжения
. Для напряжения 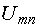 она направлена отточки m к точке n. Если мы меняем местами индексы у буквы
она направлена отточки m к точке n. Если мы меняем местами индексы у буквы 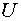 , то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как
, то следует изменить и направление стрелки на схеме. При этом при расчете меняется знак полученного напряжения, так как  .
.
Дальше записываются уравнения по второму закону Кирхгофа для любого контура, включающего в себя эту стрелку, как было сделано при расчете напряжений 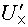 и
и 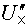 . Так, для контура m31nm при обходе его по часовой стрелке
. Так, для контура m31nm при обходе его по часовой стрелке
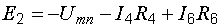 .
.
Отсюда
 . (7.1)
. (7.1)
При соответствующем навыке последняя формула может быть записана сразу, без составления уравнения второго закона Кирхгофа.
В указанном контуре напряжение 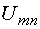 складывается из трех напряжений:
складывается из трех напряжений:
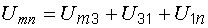 . (7.2)
. (7.2)
Порядок индексов у букв U соответствует порядку, в котором мы проходим участок электрической цепи, идя от точки m к точке n по элементам 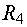 ,
, 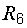 и
и 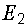 .
.
Теперь находим значение каждого слагаемого в последнем уравнении.
Величина 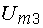 , определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении
, определяющая напряжение между точками m и 3, представляет собой падение напряжения на сопротивлении 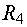 , которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока
, которое мы должны взять со знаком минус, так как от точки m к точке 3 мы идем против тока 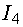 :
:
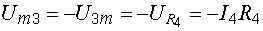 .
.
Аналогично
|
|
|
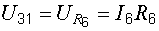 .
.
Здесь в правой части уравнения стоит плюс, так как мысленная стрелка напряжения 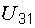 и ток
и ток 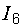 направлены в одну сторону.
направлены в одну сторону.
Третье слагаемое 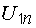 представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
представляет собой напряжение на зажимах источника. Если внутреннее сопротивление последнего равно нулю, то это напряжение по величине равно ЭДС, а знак его зависит от взаимного направления стрелок напряжения и ЭДС (рис. 7.1).
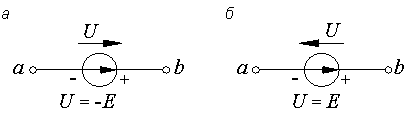
Рис. 7.1. Напряжение на зажимах источника
Рассмотрим рис. 7.1.
При указанной на схеме полярности зажимов источника потенциал точки b выше потенциала точки a на величину ЭДС:
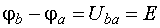 .
.
Поэтому при одинаковых направлениях стрелок 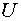 и
и  (рис. 7.1, а)
(рис. 7.1, а)
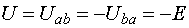 .
.
Если направления стрелок 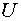 и
и  противоположны друг другу
противоположны друг другу
(рис. 7.1, б), то
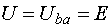 .
.
С учетом сказанного напряжение на участке 1n (см. рис. 2.1) равно
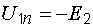 .
.
Подставляя найденные значения напряжений на участках в формулу (7.2), приходим к выражению (7.1).
То же самое напряжение, определяемое по участку m2n, будет равно
 .
.
Разумеется, вычисление одного и того же напряжения по двум различным формулам должно привести к одинаковым результатам.
ПОСТРОЕНИЕ ГРАФИКОВ
Общие требования к оформлению графиков. Зависимость мощности от тока
Правила построения графиков рассмотрим на примере зависимости мощности Р1,выделяющейся в сопротивлении первой ветви, от тока I1 в этой ветви. Эта зависимость определяется уравнением баланса мощностей в схеме рис. 6.1, в:
|
|
|
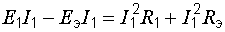 .
.
Так как 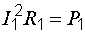 , то
, то
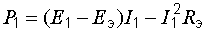 . (8.1)
. (8.1)
Это – уравнение параболы со смещенной вершиной и направленными вниз ветвями (рис. 8.1).
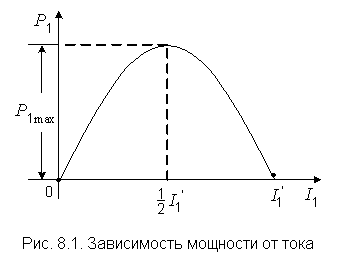
Значения тока, при которых парабола пересекает горизонтальную ось, находятся из уравнения
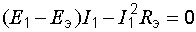
и соответственно равны
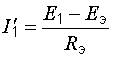 и
и 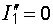 .
.
По смыслу 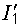 – это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении
– это ток, протекающий в схеме рис. 6.1, в при закороченном сопротивлении 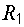 . При токе, равном половине этого значения, мощность
. При токе, равном половине этого значения, мощность 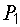 максимальна:
максимальна:
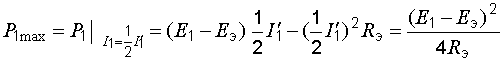 .
.
Предположим, что параметры цепи на рис. 6.1, в имеют следующие численные значения:
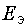 = 72,4 В;
= 72,4 В; 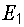 = 130 В;
= 130 В; 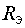 = 43,6 Ом.
= 43,6 Ом.
Прежде всего находим максимальные значения абсциссы и ординаты, которые будут определять размеры графика. В нашем примере – это значения 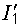 и
и 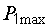 :
:
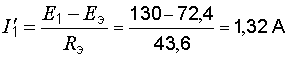 ;
;
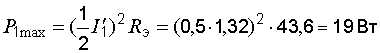 .
.
Исходя из этих величин и предполагаемых размеров графика, выбираем масштаб, который указываем на каждой оси графика в виде равномерной шкалы.
В одной единице длины (сантиметре, миллиметре) может содержаться m × 10n именованных единиц. Здесь n – целое число, положительное или отрицательное, а для mрекомендуются числа 1, 2, 5.
Положительные значения величин откладываются вправо по оси абсцисс и вверх по оси ординат.
|
|
|
В конце каждой оси ставится буквенное обозначение откладываемой величины и через запятую – ее единица измерения.
Если график строится на белой (нелинованной) бумаге, то чертится масштабная сетка.
Данные для построения графика рассчитываем по формуле (8.1) и сводим их в таблицу (табл. 8.1).
Таблица 8.1
Данные для построения графика
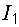 , А , А
| 0 | 0,2 | 0,4 | 0,5 | 0,6 | 0,66 | 0,8 | 0,9 | 1 | 1,2 | 1,32 |
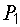 , Вт , Вт
| 0 | 9,78 | 16,1 | 17,9 | 18,9 | 19 | 18,2 | 16,5 | 14 | 6,34 | 0 |
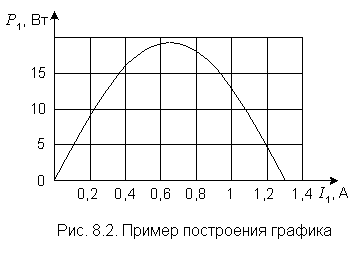
Абсциссы точек, выбираемых для построения графика, желательно располагать по оси равномерно. Но вблизи характерных областей кривой (в нашем случае у вершины параболы) точки можно взять чаще. В таблицу внесены также значения максимальной мощности и тока, которому эта мощность соответствует. При построении графика числа из таблицы на осях не показываются (рис. 8.2).
8.2. Зависимость тока от сопротивления
Зависимость тока в первой ветви от сопротивления этой ветви строим по уравнению (6.2), которое при выбранных значениях 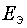 ,
, 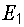 и
и 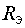 принимает вид:
принимает вид:
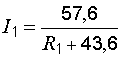 .
.
Подставляя сюда различные значения сопротивления 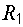 , приходим к результатам, представленным на рис. 8.3.
, приходим к результатам, представленным на рис. 8.3.
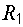 , Ом , Ом
| 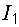 , А , А
|
| 0 | 1,32 |
| 10 | 1,07 |
| 20 | 0,91 |
| 30 | 0,78 |
| 40 | 0,69 |
| 50 | 0,62 |
| 60 | 0,56 |
| 70 | 0,51 |
| 80 | 0,47 |
|
|
|
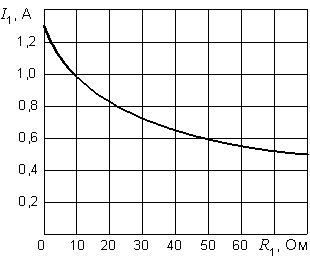
Рис. 8.3. Зависимость тока от сопротивления
Дата добавления: 2019-07-17; просмотров: 2135; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
