Обоснование и алгоритм метода скорейшего спуска решения задачи многомерной минимизации.
Пусть выбрано некот нач-е приближение 
и на некоторой итерации построено очередное приближение 
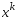и вычислены значения 
, 
. Рассм.луч, проходящий ч/з т 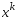в направлении антиградиента 
.В этом луче рассм. ф-ю, зависящую от альфа 
. Рассм. вспомогательную задачу одномерной минимизации 
(*).
И пусть решение этой задачи достигается в т 
: 
, тогда след. приближение вычисляется по ф-ле 
.
Итерационный процесс продолжается до тех пор, пока не будет выполнен критерий окончания счета.
В качестве критерия окончания счета могут использоваться нерав-ва:
; 
; 
,где 
, 
, 
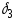–заданные числа, характеризующие точность счета
Если на некоторой итерации выполняется рав-во 
, то в т-ке хk выполн. необход. усл. Оптимальности и итерационный процесс заканчивается.
Если 
, то сущ.такое неотрицат.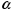 
, что 
.
Если значения 
явл. решением задачи (*), то в этой т-ке должно быть выполнено необходимое усл. оптимальности, т.е. 
Вычислим эту производную в т-ке 
Получаем, что градиенты, вычисл. в соседних приближениях, постоенных методом скорейшего спуска ортогональны.
Зам. Величину можно выбирать из условия 
, в этом случае метод наз градиентным.
Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
1)алгоритм метода условного градиента. Пусть задано начальное приближение 
и методом условного градиента вычислено 
Строим ф-цию 
и решаем задачу 
(1)
|
|
|
Пусть 
есть решение задачи. Заметим, что 
. Если 
, то 
уд. необходимому усл. и вычислительный процесс заканчивается. Если 
, то строим отрезок 
(2) на этом отрезке рассматриваем ф-цию 
и решаем задачу 
(3).
Тогда след.приближение находится по формуле 
где 
есть решение задачи (3).
Практическим критерием окончания счета выбираются нер-ва 
где 
согласованные числа, характеризующие точность счета.
Замеч1. Метод условного градиента эффективен когда вспомогат. задача (1) допускает простое решение.
Замеч2.Часто на практике задают некоторое значение 
, н/р, равное 1, проверяют усл. 
. Если оно не выполняется, то 
уменьшают, например, в два раза и т.д.
2)алгоритм метода проекции градиента. Пусть задано нач. приближение 
и методом проекции градиента вычислено 
. След.приближение ищется по формуле 
(4) В зависимости от выбора 
строятся различные варианты метода проекции градиента. Например, 
может находиться как решение задачи одномерной минимизации
(5), где 
(6)
В этом случае при 
метод проекции градиента превращается в метод скорейшего спуска.
Часто при практическом исп. метода (4) находят такое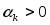 
, что выполняется условие релаксационности 
При его нарушении полагают 
равным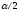 
снова проверяют условие релаксационности и т. д.
|
|
|
В качестве критерия окончания счета выбираются неравенства 
, где 
— числа, характеризующие точность счета.
Замеч4. Главная сложность реализации метода проекции градиента заключается в решении задачи проектирования.
Дата добавления: 2019-07-15; просмотров: 644; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!