Метод золотого сечения решения задачи одномерной минимизации.
Понятие решения задачи математического программирования.
Математическое программирование - это область математики, разрабатывающая теорию, решения многомерных задач с ограничениями. В отличие от классической математики, мы находим наилучший вариант из всех возможных.
Итак, математическое программирование — это раздел высшей математики, занимающийся решением задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.
Общая задача М. п. состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.
Классическая задача математического программирования – задача выбора таких значений некоторых переменных, подчиненных системе ограничений в форме равенств, при которых достигается max или min функции.
Основные определения в задаче одномерной минимизации. Примеры.
Задача одномерной минимизации состоит из двух частей:
локализации точек минимума, то есть указания отрезков, содержащих единственную точку минимума;
поиска точки минимума на заданном отрезке при наличии информации о том, что на этом отрезке заведомо существует единственный минимум.
Задача локализации минимума обычно решается с помощью классического метода, основанного на дифференциальном исчислении.
|
|
|
Кроме того, существуют и некоторые вычислительные процедуры, позволяющие в определенных условиях такую задачу решать.
В основном, ниже рассматриваются численные методы, позволяющие решать локализованные задачи.
лассический подход.
Напомним 2 важные для данного рассмотрения теоремы из классического анализа.
Теорема Вейерштрасса. Если 
непрерывна на 
, то 
существует.
Теорема Ферма. Пусть дифференцируема в точке 
. Если доставляет локальный минимум , то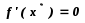 
Определение. 
называется точкой локального минимума, если существует d > 0 такое, что для 
выполняется 
Пусть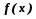 
кусочно-непрерывная и кусочно-гладкая на функция. Это означает, что на может существовать лишь конечное число точек, где 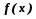терпит разрыв I-го рода, либо 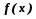непрерывна, но не имеет производной.
Тогда точками минимума могут быть такие точки, в которых:
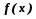- терпит разрыв;
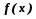- непрерывна, но 
не существует;
- 
- либо 
, либо 
.
Рисунки ниже иллюстрируют эти 4 случая.
Рисунок 3.2.1
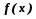терпит разрыв в точке .
Рисунок 3.2.2
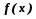непрерывна, но производной не существует.
Рисунок 3.2.3
.
Рисунок 3.2.4
.
Методы деления отрезка пополам решения задачи одномерной минимизации.
Пусть 
— действительная функция одной переменной, определенная на множестве 
. Точка 
называетсяточкой глобального минимума функции , если 
для всех 
. В этом случае 
— минимальное значение функции. Точка называетсяточкой локального минимума функции , если существует такая окрестность 
этой точки, что неравенство справедливо для всех 
. Функция называетсяунимодальной на отрезке 
, если на этом отрезке содержится единственная точка минимума. Для унимодальной функции задача минимизации корректна.
|
|
|
Решение задачи безусловной одномерной минимизации классическим методом. Если дифференцируема на 
, то необходимым условием локального минимума является условие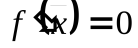 
, а точка, в которой это условие выполнено, называетсястационарной точкой. Если же дважды непрерывно дифференцируема на , то равенство 
— достаточное условие того, чтостационарная точка является точкой минимума. Как и при решении уравнений возникает необходимость локализации минимума.
Метод дихотомии (метод половинного деления): 
, 
,
, 
;
если 
, то 
и 
,
если 
, то 
и 
.
Вычисления заканчиваются когда 
.
Метод золотого сечения решения задачи одномерной минимизации.
Золотое сечение. Говорят, что внутренняя точка отрезка является точкой золотого сечения, если она делит отрезок на две неравные части так, что отношение длины большей из них к длине меньшей равно отношению длины всего отрезка к длине большей его части; величину этого отношения 
называют "золотым сечением";золотое сечениеотрезка 
осуществляют точки 
и 
.
|
|
|
Метод золотого сечения: , , 
,
, 
,
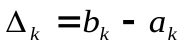если , то 
и ,
если , то и .
На очередном шаге итераций точка 
совпадает с 
или с 
. Поэтому на очередном шаге достаточно вычислить значение функции только в одной недостающей точке. Вычисления заканчиваются когда 
.
Дата добавления: 2019-07-15; просмотров: 272; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!