Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции.
Теор(о т. мин в-ой ф-ии): Пусть в задаче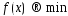 
(1) 
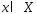-(2) ф-ия 
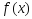выпукла, определена на выпуклом мн-ве Х, тогда:1) каждая точка ее локального минимума (если такая сущ-ет), явл-ся точкой глобального минимума;
2) Мн-во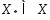 
решений задачи (1), (2) явл-ся выпуклым;3) если ф-ия 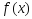строго выпукла, то она может достичь своегоmin не более чем в одной точке.
Док-во: 1) Пусть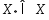 
есть точка глобальнmin ф-ии 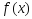, т.е. 
окрестность этой точки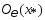 
, так что 
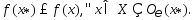Пусть 
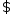точка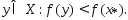 
Соединим эти точки отрезком 
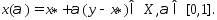Т.к. мн-во Х явл-ся выпуклым , то при всех 
: 
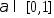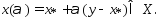
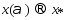при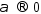 
, след-но найдется такое значение 
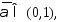что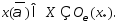 
Поэтому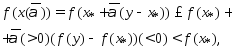 
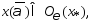что противоречит тому, что т. 
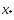явл-ся точкой локальнmin.
2) Мн-во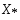 
- мн-во решений задачи 
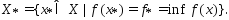Пусть мн-во 
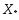состоит более чем из одной точки. Возьмем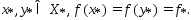 
Рассм.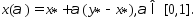 
Т.к.ф-ия 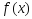-выпукла, то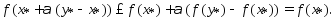 
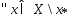выполняется нер-во
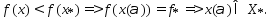
3)Предположим сущ-ет точка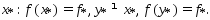 
Соединим точк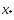и и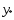 
отрезком: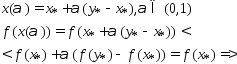 
мы нашли точку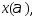 
в которой 
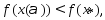что противоречит тому, что 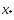явл-ся точкой локальногоmin.
Т 2 (о ст-ной точке в-ой ф-ции): Каждая стационарная точка выпуклой ф-ции 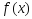, определенная на выпуклом множестве Х, явл. ее точкой минимума.
Док-во: Пусть 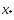стационарная точка ф-ции 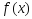, т.е. 
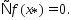Рассмотрим произвольную точку 
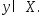Для точек 
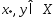в силу выпуклости ф-ции 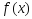выполняется: 
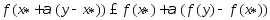(3)Т.к. ф-ция 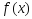дифференцируема, то приращение (из (3))=>
. 
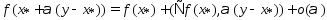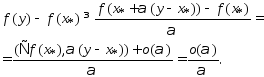по св-ву неотр
остатка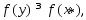 
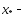точка минимума..
Необходимые условия минимума дифференцируемой функции на выпуклом множестве, выраженные через скалярное произведение. Критерий минимума выпуклой дифференцируемой функции на выпуклом множестве, сформулированный через скалярное произведение.
|
|
|
Замеч1.Если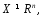 
ф-ция 
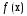дифференцируема, но не обязательно выпукла, то усл. 
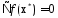может не выполняться в точке минимума ф-ции 
, т. к. возможна ситуация, когда точка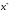 
принадлежит границе мн-ваX.
Теор1. Пусть ф-ция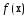 
непрерывно дифференцируема на выпуклом мн-веX. Если точка 
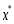явл. ее точкой минимума, то для всех 
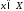выполняется нерав-во
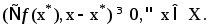(1)
Док – во. Пусть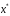 
- точка минимума ф-ции 
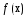. Тогда сущ. 
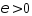, такое что 
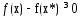для всех 
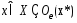. Выберем произвольную точку 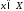и рассмотрим отрезок
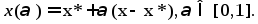
Т. к. мн-во X выпукло, то этот отрезок принадлежит мн-ву X и при малых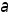 
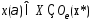. Для таких 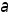рассм.
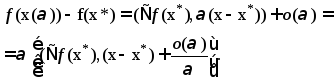(2)
Последнее выражение является неотрицательным, так как x* есть тока минимума. Но тогда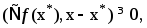 
как и в противном случае при достаточно малых 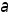приращение (3) изменит свой знак на противоположный. Теор. доказана.
Следстивие 1.Ес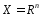ли 
или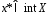 
,то нер-во (1) превращается в равенство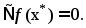 
Следствие 2.Усл(2) можно записать в виде
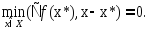(3)
Теор2. Для того, чтобы выпуклая, непрерывно дифференцируемая ф-ция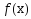 
, определенна на выпуклом, замкнутом мн-ве Х, достигала своего минимума в точке 
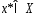, необходимо и достаточно, чтобы выполнялось нерав-во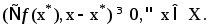
Док-во: Необходимость следует из теор1. Докажем достаточность. Пусть точка x* такова, что выполнена усл. 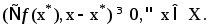Возьмем произвольную точку 
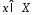и рассмотрим 
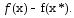По св-ву неотрицательного остатка имеем
|
|
|
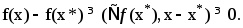
Замечание 4.Форма (3) необходимого усл. минимума непрерывно дифференцируемой ф-ции на выпуклом замкнутом мн-ве используется для построения метода усл. градиента.
Дата добавления: 2019-07-15; просмотров: 280; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!