Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Свойство Лебега выпуклых функции.

Определение 1. Множество называется отрезком прямой, соединяющим точки a и b и обозначается .

Определение 2. Множество называется выпуклым, если отрезок для любых .

Теорема 1. Пусть , - выпуклые множества. Тогда множество - выпукло.

Теорема 2. Пусть , - выпуклые множества, , . Тогда множество - выпукло.

Теорема 3. Пусть D - выпуклое множество, тогда его замыкание 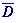также является выпуклым множеством.

Определение 3. Линейная комбинация векторов , называетсявыпуклой комбинацией, если , и .

Определение 4. Множество всевозможных выпуклых комбинаций любого конечного числа векторов из множества называется выпуклой оболочкой множества D и обозначается convD.

Очевидно, что для всякого множества , множествоconvD является выпуклым.

Множество является выпуклым тогда и только тогда, когдаD= convD.

Пересечение всех выпуклых множеств, содержащих множество D, совпадает с convD.

Определение 5. Вектор x из выпуклого множества D называется крайней точкой множества D, если он не является выпуклой комбинацией никаких двух других векторов из D.

Легко увидеть, что любая крайняя точка выпуклого множества является его граничной точкой, но не всякая граничная точка является крайней.

Выпуклые функции.

Определение 1. Функция f, определенная на выпуклом множестве , называетсявыпуклой на D, если для любых и любого выполняется неравенство , и называетсястрого выпуклой на D, если для любых , , и любого выполняется неравенство .

Определение 2. Функция f, определенная на выпуклом множестве , называется вогнутой (строго вогнутой) на D, если функция - fявляется выпуклой (строго выпуклой) на D. В случае будем говорить, чтоf выпуклая (вогнутая) функция. Очевидно, что любая строго выпуклая (строго вогнутая) функция является выпуклой (вогнутой) функцией, но не наоборот.

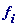Теорема 1. Для того, чтобы функция f, определенная на выпуклом множестве , была выпуклой наD, необходимо и достаточно, чтобы для любой выпуклой комбинации векторов , , выполнялось неравенство , называемое неравенством Йенсена.Теорема 2. Пусть , - выпуклые на выпуклом множестве функции, 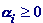, . Тогда 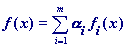- выпуклая наD функция.

Доказательство

Пусть и . Так как все функции , - выпуклые наD, то для всех выполняются неравенства Домножая эти неравенства на неотрицительные величины и суммируя их поi, получим . Следовательно . Что и требовалось доказать.

Теорема 3. Пусть 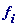, - выпуклые на выпуклом множестве функции. Тогда - выпуклая наD функция.

Доказательство

Пусть и . Так как все функции , - выпуклые наD, то для всех выполняются неравенства . Следовательно для всех . Из полученных неравентств имеем . Следовательно . Что и требовалось доказать.

Теорема 4. Пусть функция одной переменной выпуклая и неубывающая на отрезке , функция выпуклая на выпуклом множестве и для всех . Тогда - выпуклая наD функция.

Доказательство

Пусть и . Тогда 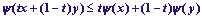в силу выпуклости наD. Очевидно, что , поэтому, в силу монотонности и выпуклости на , имеем . Следовательно . Что и требовалось доказать.

Теорема 5. Пусть - выпуклая на функция,A - матрица размерности , вектор . Тогда - выпуклая функция.

Доказательство

Пусть и . Тогда

Что и требовалось доказать.

Далее установим связь между выпуклыми множествами и выпуклыми функциями. Пусть . Обозначим .

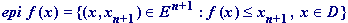Теорема 6. Пусть f - выпуклая на выпуклом множестве функция. Тогда - выпуклое множество для любого .Определение 3. Пусть f - функция, определенная на множестве . Множество называетсянадграфиком функциии f.

Теорема 7. Для того, чтобы функция f была выпуклой на выпуклом множестве , необходимо и достаточно, чтобы ее надграфик был выпуклым множеством.

Свойства выпуклых множеств

1. Пересечение любого числа выпуклых множеств является выпуклым множеством.

2. Объединение двух выпуклых множеств не обязательно выпукло.

Пример:объединение двух точек не есть выпуклое множество.

3. Геометрическая сумма , двух выпуклых множеств и , определяемая как

также является выпуклым множеством.

4. Произведение выпуклого множества на числоα, определяемое как

также является выпуклым множеством.

Эти утверждения следуют из определения выпуклого множества. Докажем,например, первое утверждение для пересечения двух множеств и . Пусть . Рассмотрим

Из выпуклости A иBполучаем, что и 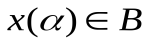при всех .Отсюда . Утверждение доказано.

Определение.Крайней (экстремальной) точкойвыпуклого множества называется такая его точка, которая не может быть представлена в виде выпуклой комбинации двух различных точек этого множества.

В качестве примера приведем выпуклый многогранник. Его крайними точками являются его вершины.

Определение. МножествоS Eⁿназываетсястрого выпуклым, если оно выпукло и все его граничные точки являются крайними.

Примером строго выпуклого множества является замкнутый шар.

Множества Лебега

определяются и в этом случае так же, как для функций в евклидовом пространстве. [1]

Имеется в виду множество Лебега, построенное в 1905 г. ( Я. [2]

Теоремы об ограниченности множеств Лебега сильно выпуклой и выпуклой функций. [3]

При этом в определении множеств Лебега можно по-прежнему считать а любым вещественным числом и нет необходимости допускать, что а может быть - f - oo или - оо. [4]

Лебегу, если все ее множества Лебега, указанные в определении 1, при любом а измеримы. [5]

Множества В 1 измеримы как множества Лебега измеримых функций, а тогда и С тоже измеримы. [6]

Отсюда видно, что все множества Лебега первого типа функции f ( х) измеримы. [7]

В следующей теореме указывается одно важное свойство множеств Лебега сильно выпуклой функции. [8]

J; % - - & все ее множества Лебега измеримы. [9]

Функция /, определенная на выпуклом множестве X, называется квазивыпуклой, если все ее множества Лебега Хрвыпуклы. [10]

Если функция f ( х), заданная на множестве Е, такова, что ее множества Лебега какого-нибудь одного типа измеримы при всех а, то эта функция измерима. [11]

В то время как оценка Sn ( x) о ( пп) имеет место в каждой точке множества Лебега [ гл. II, (11.9) ] и, в частности, в каждой точке непрерывности /, оценка Sn ( х) о ( In n) 1 / в теореме (1.2) доказана лишь почти всюду, и неизвестно, какие свойства ( не тривиальные) функции гарантируют справедливость этой оценки в заданной точке. Недостаточность простой непрерывности следует из (1.2) гл. [12]

Имеется в виду множество Лебега, построенное в 1905 г. ( Я. Куратовский установил, что это множество является проективным множеством самое большее третьего класса ( предварительное сообщение в заметке Sur un probleme concernant 1 induction transfinie. Символы tfxgfl ( А) и & & & ( А) означают классы проективных множеств; французское слово ambigu переводится как двусмысленный иди двойственный и употреблено здесь в том смысле, что множество Лебега принадлежит одновременно классам Зь Ф ( A) Ta. Нейман ( Neumann, John, von; 1903 - 1957) заметил, что проективный класс множества Лебега может быть понижен до двух. Этот результат был изложен в совместной статье К. [14]

Имеется в виду множество Лебега, построенное в 1905 г. ( Я. Куратовский установил, что это множество является проективным множеством самое большее третьего класса ( предварительное сообщение в заметке Sur un probleme concernant 1 induction transfinie. Символы tfxgfl ( А) и & & & ( А) означают классы проективных множеств; французское слово ambigu переводится как двусмысленный иди двойственный и употреблено здесь в том смысле, что множество Лебега принадлежит одновременно классам Зь Ф ( A) Ta. Нейман ( Neumann, John, von; 1903 - 1957) заметил, что проективный класс множества Лебега может быть понижен до двух.

Дата добавления: 2019-07-15; просмотров: 922; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!