Розділ ІІ . Приклади розв’язання діофантових рівнянь
Приклади розв’язання лінійних діофантових рівнянь
Задача1. Розв’язати лінійне діофантове рівняння:
3𝑥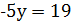 
.
Хоча одне рівняння з двома невідомими має нескінченне число розв’язків, неочевидно, що знайдеться хоча б одне з цілими додатними 𝑥 та 𝑦.
Знаючи, що 𝑥 та 𝑦 є цілими і додатними розв’яжемо це рівняння. Виділимо невідоме, коефіцієнт, якого менший, отримаємо:
,
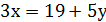звідки
.
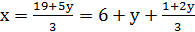Оскільки 𝑥, 6 і 𝑦 – цілі числа, то рівність може бути вірною лише за умови, що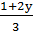 
є цілим числом. Позначимо його буквою 𝑡. Тоді
,
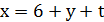де
,
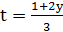і значить,
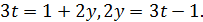
Із останнього рівняння визначаємо 𝑦:
.
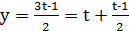Оскільки 𝑦 та 𝑡 – цілі числа, то і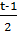 
повинно бути деяким цілим числом 
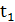. Тоді,
,
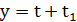причому
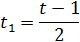
звідки
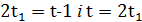+1.
Значення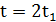 
+1 підставимо в попередні рівності:
.
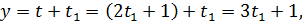
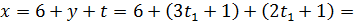
І так, для 𝑥 та 𝑦 ми знайшли представлення:
,
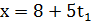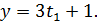
Взагалі кажучи, ми довели тільки те, що всякий цілочисельний розв'язок рівняння 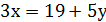, має вигляд , 
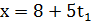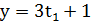, де 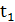- деяке ціле число. Доведення того, що при довільному цілому 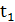ми отримаємо деякий цілочисельний розв'язок даного рівняння, випливає, якщо провести аналогічні міркування в зворотному напрямку, підставивши знайдені значення 𝑥 та 𝑦 в початкове рівняння.
Оскільки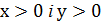 
, то і
,
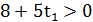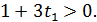
З цих нерівностей знаходимо:
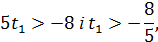
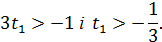
Цим самим величина 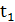обмежується; вона більша за 
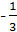(а значить і більша за 
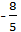). Але оскільки 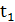- ціле і додатне число, то можна стверджувати, що для нього можливі лише наступні значення:
|
|
|
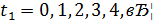
Тоді відповідні значення для 𝑥 та 𝑦 будуть такими:
,
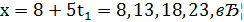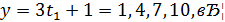
Формули для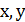 
визначають розв’язки даного рівняння у цілих невідємниних числах.
Задача2. Розв’язати систему лінійних діофантових рівнянь:
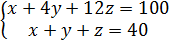
Розв'язок:
Віднявши друге рівняння від першого, отримаємо одне рівняння з двома невідомими:
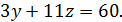
Знаходимо 𝑦:
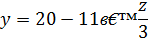
Очевидно, 
- ціле число. Позначимо його через 𝑡. Маємо:
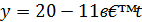
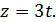
Підставляємо вирази для 𝑦 та 𝑧 у друге із початкових рівнянь:
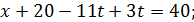
Отримаємо:
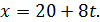
Так як 
неважко встановити межі для 𝑡:
,
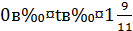З цього можемо зробити висновок, що для 𝑡 можливі тільки два цілих значення: 𝑡=0, 𝑡=1.
Відповідні значення 𝑥, 𝑦 і 𝑧 будуть такими:
| 𝑡=0 | 0 | 1 |
| 𝑥=0 | 20 | 28 |
| 𝑦=0 | 20 | 0 |
| 𝑧=0 | 0 | 3 |
Перевірка
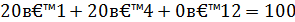
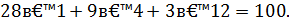
Задача3.
Вміння розв’язувати діофантові рівняння дає можливість виконати наступний математичний фокус.
Якщо помножити дату свого дня народження на 12, а номер місяця на 31 і знайти суму, то за такою сумою можна визначити дату народження.
|
|
|
Якщо, наприклад, задумана дата – 9 лютого, то наступні дії будуть такими:
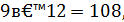
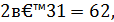
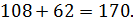
За останнім числом 170 потрібно визначити задуману дату.
Задача зводиться до розв'язку рівняння з двома невідомими
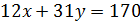
у цілих, додатних числах, причому число місяця 𝑥 не більше 31, а номер місяця 𝑦 не більше 12.
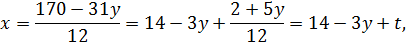
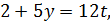
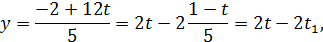
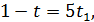
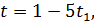
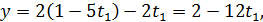
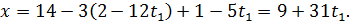
Знаючи, що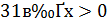 
і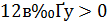 
, знаходимо межі для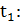 
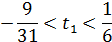
Отже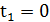 
, 𝑥=9, 𝑦=2.
Таким чином, дата народження 9-те число другого місяця, тобто 9 лютого.
Задача4.
Над двома цілими додатними числами були виконані наступні дії:
1. Їх додали;
2. Відняли від більшого менше;
3. Перемножили;
Поділили більше на менше.
Дата добавления: 2019-07-15; просмотров: 158; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!