Невизначені рівняння вищих порядків
2.1 Рівняння 
. Піфагорові трійки
Розв'язок невизначеного рівняння в цілих числах.
Можна взяти 𝑥, 𝑦, 𝑧 такими, що вони не мають спільного дільника, більшого за одиницю, інакше можна було б одразу скоротити обидві частини рівняння на квадрат цього множника. Із таких міркувань випливає, що 𝑥, 𝑦, 𝑧 є попарно взаємно простими, бо якщо, наприклад 𝑥, 𝑦 ділились на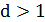 
, то і 𝑧 ділилось би на 𝑑. Таким чином, одне з чисел 𝑥, 𝑦 повинно бути непарним. Легко бачити, що інше має бути парним. Інакше в протилежному випадку, якщо б 
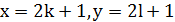, то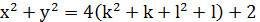 
ділилось на 2, але не ділилось би на 4 і тому не було б квадратом.(Якщо 
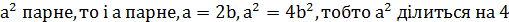. Таким чином квадрат не може ділитися на 2 і не ділитися на 4 одночасно).
Нехай 𝑥 – парне, 𝑦 – непарне, тоді 𝑧 – непарне. Візьмемо
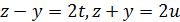
отримаємо 
.
𝑡 і 𝑢 – взаємно прості. Дійсно, якщо 𝑡 і 𝑢 мали спільний множник 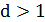, то 𝑑 містився б в 
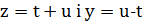, а це неможливо, бо 𝑦 та 𝑧 є взаємно простими.
Тому 𝑡 та 𝑢 повинні бути порізну точними квадратами. Доведемо це. Для цього скористаємось теоремою про розклад чисел на прості множники. Маємо
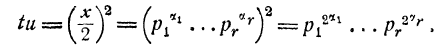
Таким чином, в силу наслідків із теореми про розклад отримуємо
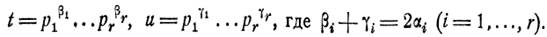
Але так як 𝑡 та 𝑢 взаємно прості, то для кожного 𝑖 одне із чисел 
дорівнює нулю і тому інше дорівнюватиме 
. Отже, всі показники в розкладах чисел 𝑡 та 𝑢 парні, звідки випливає, що кожне із цих чисел є точним квадратом:
|
|
|
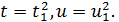
Звідси
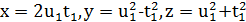(5)
Таким чином кожен розв'язок рівняння у взаємно простих цілих числах повинен представлятись у вигляді (5), де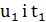 
- взаємно прості цілі числа, із яких одне парне, а інше не парне (інакше 𝑦 і 
були б парними одночасно). І навпаки, якими не були б взаємно прості цілі числа
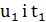різної парності, числа 𝑥, 𝑦, 𝑧 – складені з них по формулам (5) і дають розв’язки рівняння у взаємно простих числах. Дійсно, перш за все
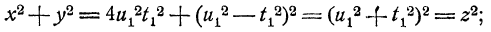
Крім того , якщо б 𝑦 та ділились на просте число 𝑑, то також
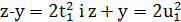ділись би на 𝑑, і так, як 𝑑 не може дорівнювати 2 (бо в силу різної парності чисел 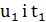, 𝑦 і 𝑧 непарні), внаслідок того, що добуток двох чисел ділиться на просте число, то одне із чисел обов’язково ділиться на цей простий дільник, випливає ,що 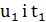повинні ділитися на 𝑑, а це суперечить тому, що числа 
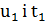є взаємно простими. Отже, 𝑦 та 𝑧, а також і вся трійка 𝑥, 𝑦,𝑧 – взаємно прості.
Таким чином формули (5) при взаємно простих 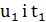різної парності, дають всі розв’язки рівняння у взаємно простих цілих числах.
Доведення теореми Ферма для четвертих степенів.
Доведемо наступну теорему:
Теорема 5.
|
|
|
Рівняння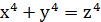 
не має розв’язків у цілих числах, відмінних від нуля, і більше того: рівняння 
не має відмінних від нуля цілих розв’язків.
Доведення.
Припустимо, що існує система відмінних від нуля розв’язків останнього рівняння. Тоді серед цих систем розв’язків повинна існувати така, для якої 𝑧 приймає найменше можливе значення. Покажемо, що 𝑥 та 𝑦 при цьому взаємно прості. Дійсно, якби 𝑥 і 𝑦 мали спільний дільник 𝑑, то 𝑧 ділилось би на 𝑑 і цілі числа 
давали б систему розв’язків з меншим 𝑧.
Як і в попередньому дослідженні рівняння , впевнюємось в тому, що із пари чисел 𝑥, 𝑦 одне повинне бути парним, а друге непарним.
Нехай 𝑥 – парне. На основі виведених вище формул (5) маємо
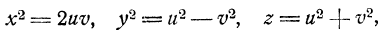
Причому 𝑢 і 𝑣 – взаємно прості числа, одне із яких парне, а інше непарне. Якщо 𝑢 було парним, 𝑣 – непарним, то 
мало б вигляд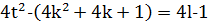 
, що неможливо, бо квадрат непарного числа завжди має вигляд 4𝑚+1. Тому 
, і так як і 𝑢 та 𝑞 взаємно прості, то аналогічно впевнюємось в тому, що
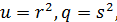
де 𝑠 і 𝑟 взаємно прості, причому 𝑟 непарне.
Рівність 
, перепишемо тепер у вигляді
,
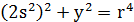де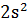 
та 𝑦 взаємно прості. Перша із цих рівностей, як і вище показує, що
|
|
|
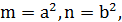а це в поєднанні з іншою рівністю дає 
.
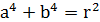Але очевидно,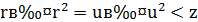 
, таким чином ми прийшли до рівняння того ж вигляду 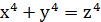, але з меншим 𝑧, що суперечить припущенню про мінімальність 𝑧.
Піфагорові трійки.
Кожний трикутник , сторонни сторони якого відносяться, як 3 : 4 : 5, згідно із загальновідомою теоремою Піфагора – прямокутний, оскільки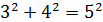 
.
Крім чисел 3, 4, 5, існує як відомо, безліч цілих додатних чисел 𝑎, 𝑏, 𝑐, які задовольняють відношення:
.
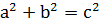Числа 𝑎, 𝑏, 𝑐 називаються піфагоровими числами. Згідно з теоремою Піфагора такі числа можуть служити довжинами сторін деякого прямокутного трикутника, тому 𝑎 і 𝑏 називають катетерами, 𝑐 – гіпотенузою.
Зрозуміло, що якщо 𝑎, 𝑏, 𝑐 є трійкою піфагорових чисел, то і 𝑝𝑎, 𝑝𝑏, 𝑝𝑐, де 𝑝 – цілий множник, - піфагорові числа. І навпаки, якщо піфагорові числа мають спільний множник, то на цей множник можна скоротити, і знову отримаємо трійку піфагорових чисел.
Тому спочатку будемо досліджувати лише трійки взаємно простих піфагорових чисел (решта отримається із їх множення на цілий множник 𝑝).
Покажемо, що в кожній із таких трійок 𝑎, 𝑏, 𝑐 один із катетів повинен бути парним, а другий непарним.
|
|
|
Міркування проводитимемо від супротивного. Якщо два катета 𝑎 та 𝑏 парні, то парним буде і число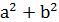 
, а значить і гіпотенуза 𝑐. Це, суперечить тому, що числа 𝑎, 𝑏, 𝑐 не мають спільних множників, так, як три парні числа мають спільний множник 2. Таким чином принаймні один із катетів повинен бути непарним. Дійсно, якщо катети мають вигляд 2𝑥+1 та 2𝑦+1, то сума їх квадратів рівна
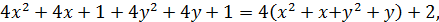
тобто представляє собою число, яке при діленні на 4 дає в остачі 2. Між іншим квадрат всякого парного числа повинен ділитися на 4 без остачі. Значить, сума квадратів двох непарних чисел не може бути квадратом парного числа, інакше кажучи, наші три числа не піфагорові.
Отже із катетів 𝑎, 𝑏 один парний, а інший непарний. Тому число 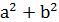непарне, а значить непарна і гіпотенуза 𝑐.
Припустимо, для визначеності, що непарним є катет 𝑎, а парним 𝑏. Із рівності
.
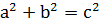ми легко отримаємо:
.
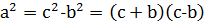Множники 
, правої частини рівності, взаємно прості. Дійсно, якщо б ці числа мали спільний множник, відмінний від одиниці, то на цей множник ділилась би і сума
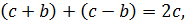
І різниця
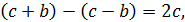
І добуток
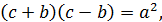
Тобто числа 2𝑐, 2𝑏, і 𝑎 мали б спільний множник. Так як 𝑎 непарне, то цей множник відмінний від двійки, і тому цей же множник мають числа 𝑎, 𝑏, 𝑐, чого бути не може.
Отримана суперечність показує, що числа 
взаємно прості.
Але якщо добуток взаємно простих чисел є точним квадратом, то кожне із них є квадратом, тобто
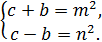
Розв’язавши цю систему, знайдемо:
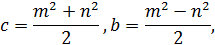
Отже розглядувані піфагорові числа мають вигляд
Де 𝑚 та 𝑛 – деякі взаємно прості непарні числа. Легко впевнитись в тому, що при будь яких таких 𝑚, 𝑛 ми отримаємо трійки піфагорових чисел. Розглянемо деякі піфагорові трійки, отримані при певних значеннях 𝑚 та 𝑛:
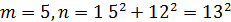
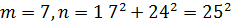
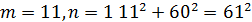
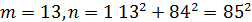
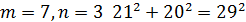
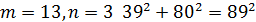
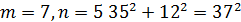
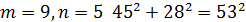
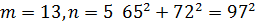
Всі інші трійки піфагорових чисел або мають спільні множники, або містять числа більше ста.
Невизначене рівняння Ферма
Розглянемо тепер рівняння вигляду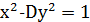 
(6).
Рівняння (6) називають невизначеним рівнянням Ферма, яке має велике значення у всій теорії діофантових рівнянь. Ми доведемо, що при кожному натуральному значенні 𝐷, відмінному від повного квадрата, це рівняння має нескінченно багато розв’язків в цілих числах, і знайдемо загальний метод знаходження всіх його розв’язків.
Теорема 6.
Нехай 𝐷 – ціле додатне, вільне від квадратів число і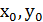 
( 
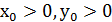) – розв'язок діофантового рівняння (6), тоді 
є чисельником і знаменником відповідно одного із підхідних дробів до 
.
Доведення. Із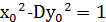 
випливає, що 
і
,
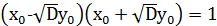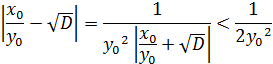
Тобто 
– однин із підхідних дробів до . Оскільки , щозадовольняють рівняння (6) є взаємно простими числами, то із рівності
випливає: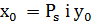 
= 
.
Розклад в ланцюговий дріб в загальному виглядає так:
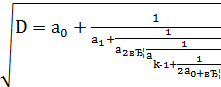(7)
Виявляється, що розв’язками рівняння (6) можуть бути чисельники і знаменники тільки тих підхідних дробів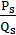 
до у яких індекс 𝑠 має вид 
.
Теорема 7.
Якщо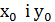 
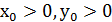( ) – розв'язок діофантового рівняння (6), то 
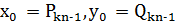, де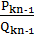 
- підхідний дріб до .
Доведення. В попередній теоремі було доведено, що якщо пара цілих додатних чисел 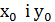є розв’язком рівняння (6), то 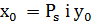= , де 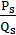- підхідний дріб до 
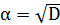. Число 
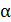є коренем квадратного рівняння з цілими коефіцієнтами
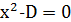. (8)
Повний частковий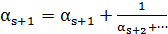 
розклад в ланцюговий дріб є коренем деякого квадратного рівняння
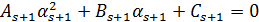
з тим же дискримінантом, як у рівнянні (8) (при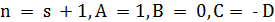 
) маємо:
;
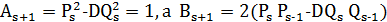- парне число, яке позначимо - 2 
. Розв’язуючи квадратне рівняння для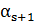 
,отримаємо 
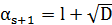, тобто розклад 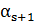в ланцюговий дріб повинен мати той же період, як і в розкладі (7) числа і відрізняється від нього тільки на перший член розладу. Це може бути тільки при 
, 
, 
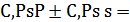
. Тепер залишається тільки вияснити, які саме з чисел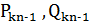 
є розв’язками рівняння (6).
Теорема.
Нехай 𝐷 – ціле додатне, вільне від квадратів число, 𝑘 – довжина періоду розкладу в ланцюговий дріб. Ми отримаємо всі розв’язки рівняння (6) в цілих додатних числах 𝑥 та 𝑦, якщо візьмемо:
де 𝑛 – довільне натуральне число, таке, що 𝑘𝑛 парне.
Доведення.
В попередній теоремі було встановлено, що всі цілі додатні розв’язки рівняння (6) знаходяться серед пар вигляду 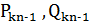. Залишається тільки вияснити, при яких 𝑛 числа 
задовольняють рівняння (6).
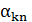врозкладі в ланцюговий дріб має вигляд:
,
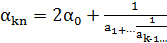тобто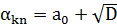 
(8).
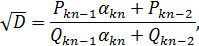
Так, що підставляючи значення 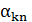із формули (8), отримаємо:
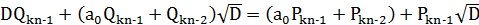(9)
Оскільки - ірраціональне, із рівності (9) випливає:
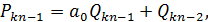
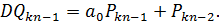
Помноживши першу з цих рівностей на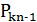 
, а другу на 
і віднявши їх, отримаємо:
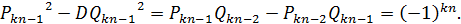
Пара 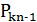, буде розв’язком рівняння (6) тоді і тільки тоді, коли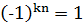 
, тобто при парних значеннях 𝑘𝑛. Найменшими додатними значеннями 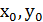, які задовольняють рівняння Ферма (6) є:
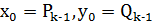, якщо 𝑘 парне.
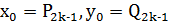, якщо 𝑘 непарне.
Приклад. 1) знайти найменші цілі додатні значення 𝑥, 𝑦, які задовольняють рівняння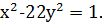 
Розкладаючи 
в ланцюговий дріб, отримуємо:
У даному прикладі 𝑘 = 6 – парне число, тому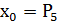 
, 
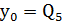- шукані значення 𝑥 та 𝑦. Обчислюючи , знаходимо 
, 
.
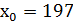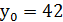2) знайти найменші цілі, додатні значення 𝑥, 𝑦, які задовольняють рівняння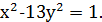 
Розкладаючи в ланцюговий дріб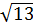 
отримуємо:
У цьому прикладі 𝑘=5, найменше парне 𝑘𝑛 дорівнює 10, тому шукані значення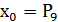 
, 
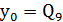. Обраховуючи, отримуємо 
, 
.
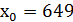Аналогічно до рівняння (6) можна розв’язати рівняння
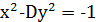. (10)
Теореми доведені для рівняння (6) справедливі і для рівняння (10), але замість умови парності 𝑘𝑛 , треба поставити умову 𝑘𝑛 не ділиться на 2. Таким чином, при парних значеннях 𝑘 діофантове рівняння (10) не має розв’язків.
2.3 Невизначене рівняння третього степеня
Сума кубів трьох цілих чисел може бути кубом четвертого числа. Наприклад,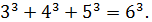 
Це означає, що куб ребро якого дорівнює 6 см, рівновеликий сумі трьох кубів, ребра яких дорівнюють 3см, 4см, 5см.
Спробуємо знайти таке ж відношення, тобто поставимо задачу: знайти розв’язки рівняння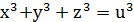 
. Зручніше позначити невідоме 𝑢 через 
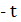. Тоді рівняння буде мати більш простий вигляд
.
Розглянемо прийом, що дозволяє знайти безліч розв’язків цього рівняння в цілих (додатних та від’ємних)числах. Нехай 𝑎, 𝑏, 𝑐, 𝑑 та 𝛼, 𝛽, 𝛾, 𝛿 – дві четвірки чисел, що задовольняють рівняння. Додамо до чисел першої четвірки числа другої четвірки, помноженої на деяке число 𝑘, і спробуємо підібрати число 𝑘 так, щоб отримані числа
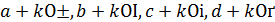
також задовольняють наше рівняння. Інакше кажучи, підберемо 𝑘 таким чином, щоб виконувалась рівність
.
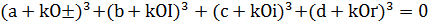Розкривши дужки і знаючи, що 𝑎, 𝑏, 𝑐, 𝑑 та 𝛼, 𝛽, 𝛾, 𝛿 задовольняють рівняння, тобто мають місце рівності
, 
,
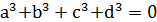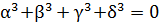ми отримаємо:
Або
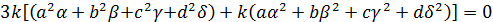
Добуто може бути нулем тоді і тільки тоді, коли є нулем принаймні один із множників. Прирівнявши кожен із множників до нуля, отримуємо два значення для 𝑘. Перше значення, 𝑘=0, нас не цікавить, бо в цьому разі отримуємо числа 𝑎, 𝑏, 𝑐, 𝑑, які задовольняють наше рівняння. Тому візьмемо інше значення для 𝑘:
Отже, знаючи дві четвірки чисел, які задовольняють початкове рівняння, можна знайти нову четвірку: для цього треба до чисел першої четвірки додати числа другої четвірки, помножені на 𝑘, де 𝑘 має вище вказане значення.
Для того щоб застосувати цей прийом, треба знати дві четвірки, що задовольняють початкове рівняння. Одну таку четвірку ми вже знаємо – (3, 4, 5,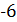 
). За другу четвірку можна взяти числа 
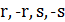, які очевидно, що задовольняють початкове рівняння. Інакше кажучи, покладемо:
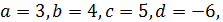
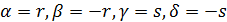
Тоді для 𝑘 ми отримаємо наступне значення:
а числа
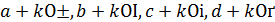
будуть відповідно дорівнювати
Очевидно, що останні чотири вирази задовольняють початкове рівняння
.
Оскільки всі ці вирази мають однаковий знаменник, то його можна відкинути. Отже при наше рівняння задовольняють (при будь яких 𝑟 та 𝑠 ) наступні числа:
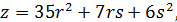
В цьому можна впевнитись і безпосередньо, піднісши ці вирази до кубу і додавши їх. Надаючи 𝑟 та 𝑠 різні цілі значення, можемо отримати цілий ряд цілочисельних розв’язків нашого рівняння. Якщо при цьому отримані числа будуть мати спільний множник, то на нього ці числа можна поділити. Наприклад, при 𝑟=1, 𝑠=1 отримуємо для 𝑥, 𝑦, 𝑧, 𝑡 наступні значення: 36, 6, 48,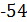 
, або після скорочення на 6, значення 6, 1, 8, 
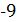. Таким чином,
.
Теорема Лежандра
Розглянемо невизначене рівняння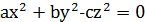 
(11). Вперше знайшов розв’язки рівняння (11) Лежандр, довівши наступну теорему:
Теорема 8.
Якщо 𝑎 , 𝑏 і 𝑐 – попарно взаємно прості додатні цілі числа, вільні від квадратів, то невизначене рівняння
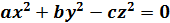
Має нетривіальні розв’язки в цілих числах 𝑥 , 𝑦 і 𝑧 , тоді і тільки тоді, коли мають розв’язки конгруенції
(12)
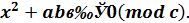
Доведення.
Необхідність умов (12) очевидна. Доведемо їх достатність.
Нехай 𝑝 – довільний непарний простий дільник числа 𝑐. Тоді із (12) випливає, що конгруенція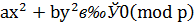 
маж нетривіальний розв'язок, наприклад, 
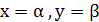. В такому випадку форма 
розкладається по модулю 𝑝 на лінійні множники:
.
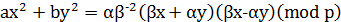Такий же розклад правильний для форми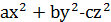 
, тобто має місце рівність
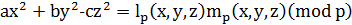, (13)
де 
- цілочисельні лінійні форми. Аналогічні рівності мають місці і для непарних простих дільників 𝑝 коефіцієнтів 𝑎 і 𝑏, а також 𝑝 = 2, так, як
.
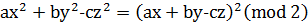Знайдемо тепер такі лінійні форми 
, щоб виконувались рівності
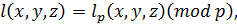
Для всіх простих дільників 𝑝 коефіцієнтів 𝑎, 𝑏 і 𝑐. Тоді із рівності (13) отримаємо
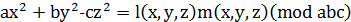, (14)
Будемо надавати змінним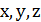 
цілі значення, які задовольняють умови
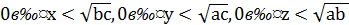(15)
Якщо виключити із розгляду тривіальний випадок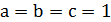 
(для нього твердження теореми очевидне), то із того, що числа 𝑎, 𝑏 і 𝑐 є взаємно простими, випливає що не всі числа 
, 
, 
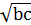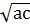будуть цілими. Значить, число наборів (𝑥, 𝑦, 𝑧), що задовольняють умови (15), строго більше, ніж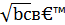 
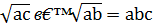. Розглянемо значення, які приймає лінійна форма 
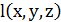при цих значеннях змінних. Так, як число наборів (𝑥, 𝑦, 𝑧) з умовою (15) більше числа лишків по модулю 𝑎𝑏𝑐, то для двох різних наборів ( 
, 
, 
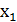) і ( 
, 
, 
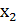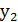) маємо
𝑙( , , )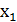 
Звідси, в силу лінійності форми 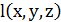, отримаємо, що при 
, 
, 
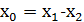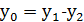виконується конгруенція
𝑙(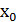 
, 
, 
) 
.
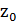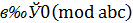Відповідно до (14),
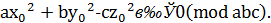(16)
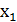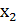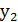Оскільки для наборів ( , , ) і ( , , ) виконується (15), то
,
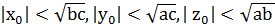Значить,
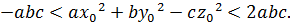
Остання нерівність сумісна із конгруенцією (16) лише в тому випадку, коли
або коли
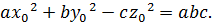
Перший випадок дає нетривіальний розв'язок, ( 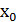, , 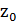). У другому випадку існування нетривіального цілочисельного розв’язку рівняння (11) випливає із тотожності
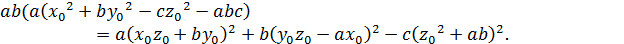
Вище доведене дає ефективний алгоритм для знаходження нетривіального цілочисельного розв'язку рівняння (11).
Дата добавления: 2019-07-15; просмотров: 124; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!