Має розв’язки в цілих числах.
Доведення.
Позначимо через М множину тих додатних цілих чисел 𝑏, для яких рівняння
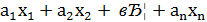 =𝑏
=𝑏
Має розв’язки в цілих числах. Множина М, очевидно, не порожня, оскільки при заданих 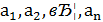 можна підібрати цілі значення
можна підібрати цілі значення  , так щоб
, так щоб 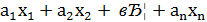 було додатним числом.
було додатним числом.
В множині М існує найменше число, яке ми позначимо через 𝑑 (𝑑 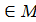 ). позначимо через
). позначимо через 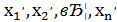 , цілі числа такі, що
, цілі числа такі, що
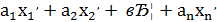 =𝑑.
=𝑑.
Нехай  =𝑏𝑞+𝑟, де
=𝑏𝑞+𝑟, де 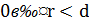 ; тоді
; тоді
 .
.
Ми підібрали цілі значення:  , такі, що
, такі, що 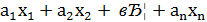 = 𝑟, але
= 𝑟, але 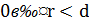 , а 𝑑 – найменше додатне число в М, тобто 𝑟 не може бути додатним, 𝑟
, а 𝑑 – найменше додатне число в М, тобто 𝑟 не може бути додатним, 𝑟 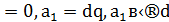 .
.
Аналогічно отримуємо 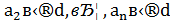 .
.
Ми бачимо, що 𝑑 – спільний дільник чисел 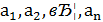 . Отже, оскільки (
. Отже, оскільки ( 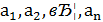 ) = 1, 1
) = 1, 1 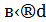 , 𝑑 = 1, 1
, 𝑑 = 1, 1 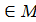 , то рівняння (2) розв’язне в цілих числах. Теорему доведено.
, то рівняння (2) розв’язне в цілих числах. Теорему доведено.
Теорема 2
Нехай 𝑑 – найбільший спільний дільник коефіцієнтів  . Діофантове рівняння
. Діофантове рівняння
 =1
=1
має розв’язки тоді і тільки тоді, коли 𝑏 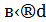 . Кількість розв’язків такого рівняння дорівнює нулю, або нескінченності.
. Кількість розв’язків такого рівняння дорівнює нулю, або нескінченності.
Доведення.
Доведемо послідовно три твердження теореми.
1) Нехай 𝑏 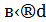 . Для рівняння
. Для рівняння

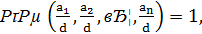 існують цілі числа:
існують цілі числа:  , які задовольняють його, тобто такі, що
, які задовольняють його, тобто такі, що

Тоді
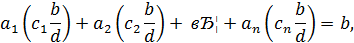
тобто 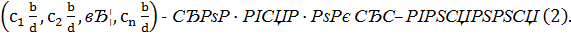
2) Нехай тепер  . Тоді ліва частина рівняння (2) при будь-яких цілих значеннях
. Тоді ліва частина рівняння (2) при будь-яких цілих значеннях 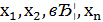 ділиться на 𝑑, а права частина на 𝑑 не ділиться, так, що рівність (2) при цілих значеннях
ділиться на 𝑑, а права частина на 𝑑 не ділиться, так, що рівність (2) при цілих значеннях 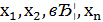 неможлива.
неможлива.
3) Якщо 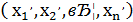 - набір чисел, які задовольняють рівняння (2), то, наприклад, всі набори
- набір чисел, які задовольняють рівняння (2), то, наприклад, всі набори 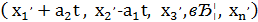 при
при 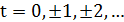 також задовольняють дане рівняння і, таким чином, у нас або взагалі не буде розв’язків , або їх буде безліч.
також задовольняють дане рівняння і, таким чином, у нас або взагалі не буде розв’язків , або їх буде безліч.
|
|
|
Якщо хоча б одна пара коефіцієнтів взаємно прості числа, то 𝑑 = 1, і рівняння (2) має нескінченну кількість розв’язків.
Приклад.
1. Діофантове рівняння 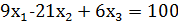 не має розв’язків , бо у даному випадку 𝑑 = 3 і 100 не ділиться на 3.
не має розв’язків , бо у даному випадку 𝑑 = 3 і 100 не ділиться на 3.
2. Діофантове рівняння 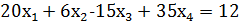 має нескінченну кількість розв’язків, оскільки 𝑑 = 1.
має нескінченну кількість розв’язків, оскільки 𝑑 = 1.
Теорема 3.
Якщо 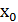 задовольняє конгруенцію
задовольняє конгруенцію
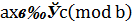 ,
,
то 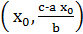 є розв’язком діофантового рівняння
є розв’язком діофантового рівняння
 (4)
(4)
Доведення.
Із  випливає, що
випливає, що  - ціле число, і безпосередня підстановка показує, що
- ціле число, і безпосередня підстановка показує, що
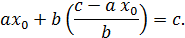
Теорема 4.
Нехай 𝑑 – найбільший спільний дільник чисел 𝑎 і 𝑏 , де 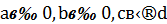 і
і 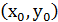 - деякий розв'язок діофантового рівняння:
- деякий розв'язок діофантового рівняння:

Тоді множина розв’язків рівняння (4) в цілих числах співпадає з множиною пар чисел ( 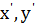 ), де
), де 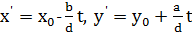 , а 𝑡 – будь-яке ціле число.
, а 𝑡 – будь-яке ціле число.
Доведення.
Нехай 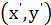 - довільний розв'язок діофантового рівняння (4), тобто
- довільний розв'язок діофантового рівняння (4), тобто 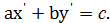 (5)
(5)
за умовою 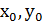 задовольняють рівняння (4), тобто
задовольняють рівняння (4), тобто 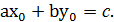
віднявши від рівності (5) останню рівність і поділивши все на 𝑑, отримаємо:
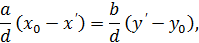
де  і
і  – цілі числа. Тоді
– цілі числа. Тоді 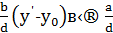 , причому
, причому 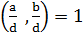 , маємо
, маємо  ,
,  ,
, 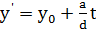 , де 𝑡 – деяке ціле число. Підставляючи знайдене значення
, де 𝑡 – деяке ціле число. Підставляючи знайдене значення  в (5), отримаємо:
в (5), отримаємо:
|
|
|

звідки 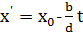 .
.
Таким чином, будь-який розв'язок рівняння (4) буде мати вигляд:
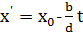 ,
, 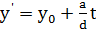 ,
,
де 𝑡 – деяке ціле число.
Обернене твердження також правильне. Нехай 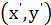 такий набір пар чисел, що
такий набір пар чисел, що
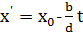 ,
, 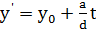 .
.
Безпосередня перевірка показує, що

Тобто 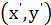 - розв'язок діофантового рівняння (4).
- розв'язок діофантового рівняння (4).
Зауваження.
Теорема правильнаі тоді, коли 𝑎 і 𝑏 дорівнюють нулю. Наприклад, при 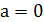 , тобто у випадку рівняння
, тобто у випадку рівняння 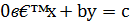 , отримуємо
, отримуємо 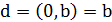 і при
і при 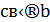 для 𝑦 існує єдине значення
для 𝑦 існує єдине значення 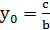 , а 𝑥 – довільне ціле. Будь-який розв'язок цього рівняння можна представити у вигляді
, а 𝑥 – довільне ціле. Будь-який розв'язок цього рівняння можна представити у вигляді 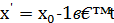 ,
, 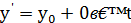 , і при будь-якому 𝑡 такі
, і при будь-якому 𝑡 такі  задовольняють рівняння
задовольняють рівняння 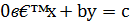 .
.
Приклад.
Розв’язати рівняння 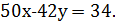
У цьому рівнянні (50, 42) = 2. 34 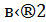 . Розглянувши конгруенцію
. Розглянувши конгруенцію 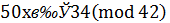 знаходимо:
знаходимо:

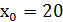 , так що 25
, так що 25 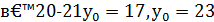 .
.
Будь-який розв'язок даного діофантового рівняння має вигляд:
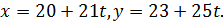
Дата добавления: 2019-07-15; просмотров: 135; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
