Знаходження рішень рівнянь трафіка
Позитивність рішення рівнянь трафіка для досить загальної моделі доведена в роботі [9].
Для знаходження рішень рівнянь трафіка складемо рівняння відносно 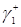 . Для цього перетворимо формулу (3.1.12), перенесемо все в ліву частину й приведемо до загального знаменника
. Для цього перетворимо формулу (3.1.12), перенесемо все в ліву частину й приведемо до загального знаменника
 . (3.2.1)
. (3.2.1)
Тому що  , те формула (3.2.1) прийме наступний вид
, те формула (3.2.1) прийме наступний вид
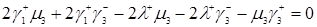 . (3.2.2)
. (3.2.2)
Підставляючи формулу (3.1.14) і (3.1.15) в (3.1.16) маємо
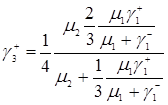 .
.
Приводимо до загального знаменника
 . (3.2.3)
. (3.2.3)
Підставимо формулу, отриману з формули (3.1.13) відрахуванням формули (3.1.12), одержимо 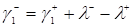 , у формулу (3.2.3), одержимо
, у формулу (3.2.3), одержимо
 ,
,
 . (3.2.4)
. (3.2.4)
Позначимо  й
й  , тоді
, тоді
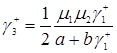 . (3.2.5)
. (3.2.5)
Відповідно до формул (3.1.16) і (3.1.17)
 . (3.2.6)
. (3.2.6)
З огляду на формулу (3.2.6) і (3.2.5), одержимо
 . (3.2.7)
. (3.2.7)
Підставимо формули (3.2.5) і (3.2.6) у формулу (3.2.2), маємо
 . (3.2.8)
. (3.2.8)
Тому що  , те формула (3.2.8) прийме наступний вид
, те формула (3.2.8) прийме наступний вид
 .
.
Розкриваючи дужки й приводячи подібні члени, запишемо формулу (3.2.9) у вигляді
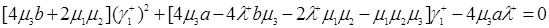
Таким чином, отримане рівняння (3.2.10) квадратне, тобто
 , (3.2.11)
, (3.2.11)
|
|
|
де коефіцієнти  , з огляду на позначення
, з огляду на позначення  й формулу (3.2.10), визначаються в такий спосіб
й формулу (3.2.10), визначаються в такий спосіб
 , (3.2.12)
, (3.2.12)

 , (3.2.13)
, (3.2.13)
 . (3.2.14)
. (3.2.14)
Для рівняння (3.2.11) знайдемо дискримінант, з огляду на формули (3.2.12), (3.2.13), (3.2.14), маємо

 .
.
Для одержання рішення рівняння (3.2.11) повинне виконаються наступна умова 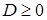 , а це можливо тоді, коли
, а це можливо тоді, коли
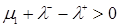 .
.
Відповідно до формули  , одержимо
, одержимо
 ,
,
тобто
 . (3.2.15)
. (3.2.15)
Відповідно до малюнка 3.1, формула (3.2.15) є умову ергодичності. Якщо ця умова не виконується, то немає стаціонарного розподілу.
З огляду на формули (3.2.12), (3.2.14), (3.2.15) одержимо, що  ,
, 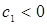 . Відповідно до зворотної теореми Вієта, якщо
. Відповідно до зворотної теореми Вієта, якщо 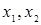 - корінь рівняння (3.2.11), те виконуються наступні співвідношення
- корінь рівняння (3.2.11), те виконуються наступні співвідношення


Тому що  , те одне з корінь позитивний і один негативний.
, те одне з корінь позитивний і один негативний.
Таким чином, рівняння (3.2.11) має одне позитивне рішення. Тобто система рівнянь трафіка (3.1.12) - (3.1.17) має позитивне рішення.
Рівняння рівноваги
У відповідності, з малюнком 3.1 складемо рівняння рівноваги




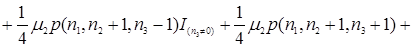
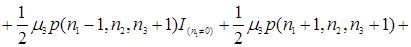

 (3.3.1)
(3.3.1)
 .
.
Визначення виду стаціонарного розподілу
Стаціонарний розподіл представимо у формі добутку множників вузли, що характеризує; кожний множник є стаціонарний розподіл вузла, тобто
|
|
|
 .
.
Стаціонарний розподіл  вузла має вигляд
вузла має вигляд
 ,
,
де
 ,
,  .
.
Таким чином, стаціонарний розподіл має такий вигляд

 . (3.4.1)
. (3.4.1)
Позначимо через
 ,
,  ,
,  .
.
Тоді в цих позначеннях формула (3.4.1) запишеться в наступному виді
 . (3.4.2)
. (3.4.2)
Підставляючи формулу (3.4.2) у рівняння рівноваги (3.3.1), одержимо

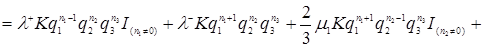
 (3.4.3)
(3.4.3)

 .
.
Розділимо обидві частини рівняння (3.4.3) на  , одержимо
, одержимо


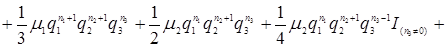
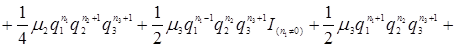 (3.4.4)
(3.4.4)
 .
.
Через  запишемо рівняння трафіка (3.1.12) – (3.1.17)
запишемо рівняння трафіка (3.1.12) – (3.1.17)
 , (3.4.5)
, (3.4.5)
 , (3.4.6)
, (3.4.6)
 , (3.4.7)
, (3.4.7)
 , (3.4.8)
, (3.4.8)
 , (3.4.9)
, (3.4.9)
 . (3.4.10)
. (3.4.10)
Тому що  , (
, (  ), те одержимо наступні співвідношення
), те одержимо наступні співвідношення
 , (3.4.11)
, (3.4.11)
 , (3.4.12)
, (3.4.12)
 . (3.4.13)
. (3.4.13)
|
|
|
Розглянемо всілякі випадки числа заявок у марковської моделі мережі із трьома вузлами й різнотипними заявками. Тобто наступні випадки
1)  ,
, 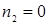 ,
,  ;
;
2)  ,
, 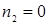 ,
,  ;
;
3)  ,
,  ,
,  ;
;
4)  ,
,  ,
,  ;
;
5)  ,
,  ,
,  ;
;
6)  ,
,  ,
,  ;
;
7)  ,
, 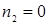 ,
,  ;
;
8)  ,
,  ,
,  ;
;
Підставляючи значення 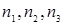 в рівняння (3.4.4), з огляду на рівняння (3.4.5) – (3.4.13), перевіримо, задовольняє стаціонарний розподіл (3.4.1) рівнянням рівноваги (3.3.1). Розглянемо кожний з випадків 1) - 8) окремо.
в рівняння (3.4.4), з огляду на рівняння (3.4.5) – (3.4.13), перевіримо, задовольняє стаціонарний розподіл (3.4.1) рівнянням рівноваги (3.3.1). Розглянемо кожний з випадків 1) - 8) окремо.
Розглянемо перший випадок  ,
,  ,
, 
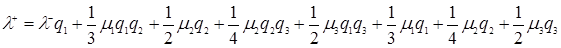 .
.
Відповідно до формули (3.4.6) 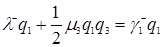 , формулі (3.4.8)
, формулі (3.4.8)  ,
,  , формулі (3.4.10)
, формулі (3.4.10)  , формулі (3.4.9)
, формулі (3.4.9)  , одержимо
, одержимо
 ,
,
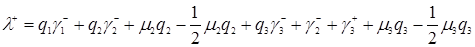 .
.
Відповідно до формули (3.4.5)  , формулою (3.4.12)
, формулою (3.4.12)  , формулою (3.4.13)
, формулою (3.4.13)  . З формул (3.4.9), (3.4.10)
. З формул (3.4.9), (3.4.10)  , тоді маємо
, тоді маємо
 ,
,
 .
.
Відповідно до формули (3.4.9)  , формулі (3.4.10)
, формулі (3.4.10)  . З формул (3.4.7) і (3.4.8)
. З формул (3.4.7) і (3.4.8)  , одержимо
, одержимо
 ,
,
 .
.
А це є формула (3.4.11), тобто випадок 1) виконується.
Розглянемо другий випадок  ,
,  ,
, 

 ,
,
Відповідно до формули (3.4.5) 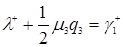 , формулі (3.4.6)
, формулі (3.4.6)  , формулі (3.4.8)
, формулі (3.4.8) 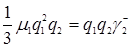 ,
,  , формулі (3.4.10)
, формулі (3.4.10)  , формулі (3.4.10)
, формулі (3.4.10)  . З формул (3.4.5) і (3.4.6)
. З формул (3.4.5) і (3.4.6)  . Розкриємо дужки й перенесемо все в праву частину, одержимо
. Розкриємо дужки й перенесемо все в праву частину, одержимо
 .
.
Відповідно до формули (3.4.13) 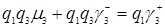 , формулою (3.4.12). З формул (3.4.9), (3.4.10)
, формулою (3.4.12). З формул (3.4.9), (3.4.10)  , тоді
, тоді
 .
.
Відповідно до формули (3.4.11)  ,
,  ,формулі (3.4.12)
,формулі (3.4.12)  . З формул (3.4.7) і (3.4.8)
. З формул (3.4.7) і (3.4.8)  , одержимо
, одержимо
|
|
|
 .
.
 , тобто випадок 2) виконується.
, тобто випадок 2) виконується.
Аналогічно виконуються 3) - 8).
Таким чином, випадки 1) – 8) перетворюються у вірну рівність. Тобто стаціонарний розподіл (3.4.1) є рішення рівняння рівноваги (3.3.1), якщо виконується умова ергодичності  ,
,  .
.
Висновок
У роботі проведене дослідження відкритих марковских і полумарковских мереж масового обслуговування із трьома вузлами й циклічною маршрутизацією.
Отримано наступні основні результати:
Для марковської моделі мережі із трьома вузлами, записані рівняння рівноваги (формула 1.1.3), отримана достатня умова ергодичності (формула 1.3.1) і знайдена стаціонарний розподіл (формула 1.2.9).
Для полумарковської моделі мережі із трьома вузлами, визначений вид диференційно-різницевих рівнянь Колмогорова (формула 2.1.4), знайдений стаціонарний розподіл (формула 2.2.1) і доведена інваріантність (див. 2.3).
Для марковської моделі мережі із трьома вузлами й різнотипними заявками, складені рівняння рівноваги (формула 3.3.1), знайдений стаціонарний розподіл (формула 3.4.1) і отримана достатня умова ергодичності (формула 3.2.15).
Результати роботи можуть бути застосовані при проектуванні й експлуатації мереж передачі даних, інформаційно-обчислювальних мереж, мереж ЕОМ і багатьох інших технічних об'єктів.
Список використаних джерел
Малинковський Ю.В. Теорія масового обслуговування. – К., 2003
Буриков А.Д., Малинковський Ю.В., Маталицкий М.А. Теорія масового обслуговування. – К., 2004
Івченко Г.И., Каштанів В.А., Коваленко И.Н. Теорія масового обслуговування. – К., 2004
Прохоров А.В., Ушаков В.Г., Ушаков Н.Г. Задачі по теорії ймовірностей: Основні поняття. Граничні теореми. Випадкові процеси. – к., 2003
Кениг Д., Штоян Д. Методи теорії масового обслуговування// Під ред. Г.П. Климова. – К., 2001
Гнеденко Б.В., Коваленко І.М. Введення в теорію масового обслуговування. – К., 2003
Ширяев О.М. Імовірність. – К., 2005
Gelenbe E. Product Form Queueing Networks with Negative and Positive Customers // J. Appl. Probab. - 1991. - V. 28. - P. 656 - 663.
Gelenbe E., Shassberger R. Stability of Product-Form G-networks // Probab. in Eng. and Inform. Sci. - 1992. - No. 6. - P. 271 - 276.
Дата добавления: 2019-07-15; просмотров: 260; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
