Полумарковська модель мережі із трьома вузлами
Нехай є відкрита мережа масового обслуговування, що складає із трьох вузлів, у яку надходить найпростіший потік заявок з параметром 
. Причому, у першу систему масового обслуговування, що входить заявка надходить із імовірністю 
. Часи обслуговування заявок в 
-ом вузлі задані функцією розподілу часу обслуговування -им приладом однієї заявки 
, 
. При цьому накладає наступна вимога
, . (2.1)
Дисципліни обслуговування заявок у системах мережі LCFS PR - заявка, що надходить в -ий вузол, витісняє заявку із приладу й починає обслуговуватися. Витиснута із приладу заявка стає в початок черги. Схематично мережа зображена на малюнку 2.1.
Стан мережі описується випадковим процесом
,
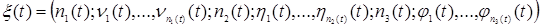де 
, 
, 
- залишковий час обслуговування заявки, що коштує в 
-ой позиції.
Примітка. Випадковий процес
,
де 
- число заявок в -ом вузлі в момент 
, не є марковським процесом. Для марковизації процесу включаємо додаткові змінні. Щоб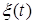 
був марковським процесом, додаткові змінні візьмемо, як залишкові часи від моменту часу до повного завершення відповідних часів. Виходить, процес 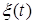- марковський процес.
Таким чином, з вищесказаного треба, що побудовано полумарковська модель відкритої мережі із трьома вузлами.
Диференційно-різницеві рівняння Колмогорова
У відповідності методом диференціальних рівнянь і малюнком 2.1, складемо наступні рівняння
|
|
|
, (2.1.1)
де 
, 
.
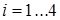Скористаємося наступними формулами:
,
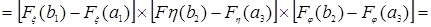
[7]
Тоді рівняння (2.1.1) запишуться в такий спосіб
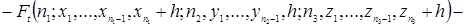
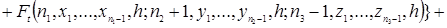
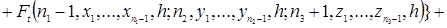(2.1.2)
Зважаючи на те, що деякі події є неможливими (вони дорівнюють нулю), рівняння (2.1.2) приймуть наступний вид
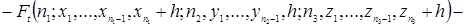
Розкладання функції 
в ряд Тейлора, має вигляд
де 
- позиція елемента 
й 
відповідно.
Використовуючи розкладання функції в ряд Тейлора, перетворимо рівняння (2.1.3)
.
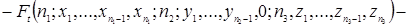
Переносимо 
в ліву частину рівності, потім ділимо обидві частини на 
й спрямовуємо 
, одержимо
(2.1.4)
.
Таким чином, рівняння (2.1.4) і є шукані рівняння Колмогорова.
Пошук рішення диференційно-різницевих рівнянь Колмогорова
Рішенням рівнянь Колмогорова (2.1.4) є:
.
Перевіримо знайдене рішення (2.2.1) безпосередньою підстановкою в рівняння (2.1.4), одержимо
Таким чином, 0=0, тобто рішення (2.2.1) задовольняє рівнянням (2.1.4).
|
|
|
Доказ інваріантності стаціонарного розподілу
Згідно 1.2, для марковської моделі мережі із трьома вузлами отриманий вид стаціонарного розподілу, що визначається по формулі (1.2.9). При цьому часи обслуговування заявок мають показовий розподіл з параметрами 
для 
-ого вузла, де 
– число заявок в 
-ой системі, 
. Відповідно до розділу 2, для полумарковської моделі мережі із трьома вузлами, припускаємо, що тривалість обслуговування окремої вимоги розподілена за довільним законом. Нехай 
– функція розподілу часу обслуговування 
-им приладом однієї заявки. Передбачається, що виконується умова, обумовлене формулою (2.1).
Відповідно до результату Севастьянова [6] і формулі (2.2.1), стаціонарний розподіл зберігає форму добутку (інваріантне) і при допущених допущеннях.
Таким чином, доведена інваріантність стаціонарного розподілу відкритої мережі масового обслуговування із трьома вузлами.
Дата добавления: 2019-07-15; просмотров: 304; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!