Орієнтирні кути та зв’язок між ними.

Предмет і завдання геодезії на сучасному етапі.

Вивчення Землі - це предмет багатьох наук про Землю, які відносяться до класу природознавчих наук. Серед них особливе місце займає одна з найстаріших наук про Землю - геодезія.

В своїх першопочатках вона виникла з потреби людей в розподілі та обліку родючих ділянок земної поверхні для їх сільськогосподарського використання. Геодезія, як поняття, походить від грецьких слів "я ділю Землю". Головні геодезичні задачі розв'язуються методами геометрії (від грецького - землевимір), тому аж до самого XVIII століття в Росії геодезистів називали геометрами. Першою книгою, набраною в Росії цивільним шрифтом, був посібник з геодезії Беркенштейна "Теометрия словенски землемерие" (1708).

Відповідно до розвитку людського суспільства виростали обсяги та складність геодезичних робіт. Різноманітність наукових і практичних завдань, які вирішуються геодезією, призвела до виділення геодезичних дисциплін, таких як: топографія, картографія, інженерна (прикладна) геодезія, фотограмметрія, вища геодезія, динамічна геодезія, космічна геодезія, геодезична астрономія, морська геодезія та ін.

Питання зйомки великих і малих ділянок земної поверхні є предметом топографії - наукової геодезичної дисципліни, яка займається детальним вивченням земної поверхні в геометричному відношенні та розробкою способів її зображення у вигляді топографічних карт і планів.

Методи зображення сферичної поверхні Землі на площині в вигляді карт та технологію їх виробництва розглядає картографія. Картографія, - за визначенням Саліщева К.А., - наука про відображення і дослідження явищ природи та суспільства, їх розміщення, властивостей взаємозв'язку і змін в часі - через картографічні моделі" [1].

Прикладна (інженерна) геодезія - це область геодезичної науки, яка займається вивченням методів геодезичних робіт при вишукуваннях, проектуванні, будівництві і експлуатації інженерних споруд, монтажі та експлуатації технологічного устаткування і т.д.

Розвиток пізнавальної діяльності, пов'язаної з визначенням форми та розмірів Землі, вивчення зовнішнього гравітаційного поля Землі, горизонтальних і вертикальних рухів її. кори, створення високоточної астрономо-геодезичної, гравіметричної та нівелірної мереж складає предмет вищої геодезії.

Значних успіхів геодезія досягла завдяки використанню зйомок земної поверхні з літаків, супутників та інших літальних апаратів для створення топографічних карт і планів.

Таким чином, сучасна геодезія являє собою багатогранну наукову дисципліну, яка вирішує складні наукові, науково-технічні і інженерні задачі через геодезичні виміри та їх інтерпретацію. Геодезія - наука про методи визначення фігури, розмірів та гравітаційного поля Землі, зображення її поверхні на планах та картах, а також способах виконання спеціальних вимірів для розв'язання різних задач народного господарства та оборони країни.

Геодезія, як одна з наук про Землю, тісно пов'язана з такими науками, як астрономія, географія, геологія, геоморфологія, геофізика. Методи розв'язання задач геодезії ґрунтуються на широкому використанні математики, фізики, інформатики та електроніки. З іншого боку, названі науки не можуть обійтись без геодезичних даних в вигляді числових характеристик просторового розміщення об'єктів на фізичній поверхні Землі.

Загальні відомості про форму і розмір З емлі.

Точні знання про фігуру та розміри Землі необхідні в різних галузях науки і техніки. Це питання має особливе значення в геодезії для зображення земної поверхні на планах та картах. Крім того такі відомості використовують при запуску штучних супутників Землі і космічних ракет, в авіації, морському плаванні, при будівництві крупних інженерних споруд і т.д.

В наш час під фігурою Землі розуміють фігуру, обмежену фізичною поверхнею Землі, тобто поверхнею її твердої оболонки на суші і поверхнею морів та океанів у їх спокійному стані.

Тривалий час за загальну фігуру Землі приймалась складна фігура, названа в 1873 р. німецьким фізиком І.Б. Лістінгом "геоїдом". Геоїд в перекладі з грецької мови означає землеподібний.

Для пояснення цієї фігури скористуємося поняттям "рівнева поверхня". Це замкнута поверхня, яка в кожній своїй точці перпендикулярна прямовисній лінії, тобто вона перпендикулярна до напряму сили тяжіння.

Рівневих поверхонь, що огинають Землю, можна уявити безліч. За основну рівневу поверхню приймається та, котра співпадає з поверхнею води в океанах і відкритих морях в спокійному стані, тобто при відсутності припливів, відпливів, течій, хвилювань і т.п. Практично за основну рівневу поверхню приймають середній рівень океану, визначений багатолітніми спостереженнями за рівнем води. Якщо основну рівневу поверхню продовжити під континентами так, що в будь-якій її точці прямовисні лінії будуть перпендикулярні до цієї поверхні, то утворюється замкнута хвиляста поверхня без складок і ребер, що охоплює все тіло Землі. Тіло, обмежене такою поверхнею, й називається геоїдом.

Таким чином, фігура геоїда визначається напрямом прямовисних ліній або, кажучи іншими словами, напрямками сили тяжіння. Ці напрямки залежать від розподілу мас в тілі Землі.

Оскільки неможливо визначити істинний розподіл мас всередині Землі, то поверхню геоїда не можна визначити точно без використання гіпотез про фізичну будову Земної кулі. Тому революційним для геодезії став розроблений радянським вченим М.С. Молоденським (1949 р.) метод точного визначення фізичної поверхні Землі, який не вимагає допоміжних гіпотез.

М.С. Молоденський запропонував визначити не фігуру геоїда (як це робилось раніше), а фігуру реальної Землі на основі геодезичних, астрономічних та гравіметричних вимірів. Для вивчення фізичної поверхні Землі ним була введена допоміжна поверхня, дуже близька до поверхні геоїда і названа квазігеоїдом.

На морях та океанах поверхні геоїда і квазігеоїда співпадають, в рівнинних районах - розходяться на декілька сантиметрів, а в гірських - не більш, як на 2 м. Тому для вирішення багатьох завдань геодезії вважають, що поверхні геоїда і квазігеоїда практично співпадають.

Поверхня геоїда в математичному відношенні є достатньо складною для вирішення практичних задач. Тому під час вивчення фігури Землі з давніх часів діють таким чином. Спочатку визначають форму і розміри деякої моделі Землі, поверхня якої відносно проста, добре вивчена в геометричному відношенні, зручна для вирішення на ній геодезичних та картографічних задач і найповніше характеризує в першому наближені форму та розміри реальної Землі. Тоді, прийнявши поверхню цієї моделі за відлікову, визначають відносно неї висоти точок реальної Землі. Поверхня, яка відповідає прийнятій моделі, називається поверхнею відносності.

При розв'язанні геодезичних задач за таку модель Землі приймають еліпсоїд обертання.

Ця фігура утворюється обертанням еліпса PEP₁E₁, навколо його малої осі РР₁, яка співпадає з віссю обертання Землі (рис. 1.1).

Розміри еліпсоїда характеризуються довжинами його півосей: а - велика піввісь, b - мала піввісь і полярним стисненням α:

Еліпсоїд обертання з малим стисненням називають сфероїдом.

Лінії перерізу поверхні сфероїда площинами, які проходять через вісь обертання РР_: , називаються меридіанами і являються еліпсами. Лінії перерізу поверхні сфероїда площинами, перпендикулярними до осі обертання, називаються паралелями і є колами. Паралель, площина якої проходить через центр сфероїда, називається екватором.

Параметри еліпсоїда мають бути такими, щоб він найближче наближався до геоїда. В випадку, коли еліпсоїд найбільш близький до фігури Землі в цілому, його називають загальним земним еліпсоїдом. В окремих країнах (або в групі країн) під час обробки геодезичних вимірів використовують еліпсоїди з параметрами, отриманими за результатами геодезичних робіт на території даної країни або декількох країн. Такі "робочі" еліпсоїди називаються референц-еліпсоїдами. Референц-еліпсоїд можна розглядати як еліпсоїд, який найближче підходить тільки до певної частини поверхні Землі.

Розміри референц-еліпсоїдів неодноразово визначались вченими різних країн. До 1946 р. в СРСР користувались еліпсоїдом, розміри якого обчисленні в 1841 р. німецьким астрономом Ф.В. Бесселем (1784-1846). Однак еліпсоїд Бесселя на більшій частині території СРСР значно відходив від геоїда. Так якщо прийняти, що поверхні геоїда і еліпсоїда Бесселя в західній частині СРСР ( Пулковська обсерваторія під Ленінградом) будуть співпадати, то відхилення цього еліпсоїда в східних областях СРСР ( Далекий схід) досягнуть 400 метрів.

Орієнтирні кути та зв’язок між ними.

Орієнтувати лінію на місцевості означає знайти її положення відносно меридіану.

Кутами, які визначають напрямок ліній, служать дирекційні кути, азимути і румби.

Дирекційним кутом називають горизонтальний кут, який відраховується за ходом годинникової стрілки від північного напрямку осьового меридіану до заданого напрямку. На практиці замість осьового меридіану часто використовують лінію паралельну до нього. Прямий і зворотній дирекційні кути однієї і тієї ж лінії відрізняються на 180°.

Істинним азимутом називається горизонтальний кут А , який відраховують за ходом годинникової стрілки від північного напрямку істинного (географічного) меридіану до заданого напрямку. Меридіани не паралельні між собою, тому в точках прямої азимути різні і їх значення відрізняються на величину g (зближення меридіанів цих точок).

Зв’язок між істинним азимутом А і дирекційним кутом a виражається формулою: A = a ± g

У формулі знак плюс або мінус залежить від знаку зближення меридіанів (якщо зближення меридіанів західне, то воно береться зі знаком мінус, якщо східне - плюс).

Магнітним азимутом A_m називається горизонтальний кут, що відраховується за ходом годинникової стрілки від північного напрямку магнітного меридіану до заданого напрямку.

Дирекційні кути та азимути змінюються від 0° до 360°.

Між магнітним та істинним меридіанами утворюється кут d, який називається магнітним схиленням. Магнітне схилення d може бути східне (рис.20,а) або західне (рис.20,б).

Зв’язок між магнітним та істинним азимутами виражається формулою:

A=A _m ± d .

На практиці часто замість дирекційних кутів і азимутів для орієнтування ліній користуються румбами.

Румбом називається гострий кут r (рис.21.), який відраховують від найближчого напрямку осьового меридіану (північного або південного) до заданого напрямку.

Румби можуть бути вираховані за значеннями дирекційних кутів

Теодоліт .

Кутові вимірювання на місцевості пов'язані з прямовисною лінією, що проходить через вершину вимірюваного кута. Для побудови планів і карт застосовуються не самі кути між лініями, а проекції кутів на горизонтальну і прямовисну площини.

Нехай на місцевості необхідно виміряти кут АВС між лініями ВА і ВС (рис. 6.1 а). Проведемо через ці лінії прямовисні площини К₁, і К₂, які перетинаються по прямовисній лінії ВВ₁, що проходить через вершину кута. Площини двогранного кута, перетинаючись з рівневою поверхнею Р, утворюють горизонтальний кут β.

З рис. 6.1 а очевидно, що такий самий кут можна отримати, якщо двогранний кут перетнути горизонтальною площиною Р₁ у довільній точці b ₁ прямовисної лінії ВВ₁. Якщо у площині Р₁ помістити кутомірний круг G і його центр з прямовисною лінією, то можна виміряти величину горизонтального кута β.

Отже, для вимірювання горизонтального кута β між лініями на місцевості необхідно побудувати дві прямовисні площини К ₁ і К₂. Можна обмежитися однією прямовисною площиною, яка обертається навколо прямовисної лінії ВВ ₁ , що проходить через вершину K вимірюваного кута.

Прямовисну площину К ₁ можна уявити як площину, що утворена лінією b ₁ А ₁ , яка може обертатися навколо горизонтальної осі і проходить через лінію ВВ ₁ (рис. 6.1 б). Якщо у площині К ₁ помістити вертикальний кутомірний круг W з центром у точці b ₁ , то можна визначити вертикальний кут нахилу лінії b ₁ А₂. Кут нахилу лінії b ₁ А₂ буде дорівнювати куту нахилу лінії ВА місцевості, якщо ці лінії паралельні.

Розглянуті геометричні елементи отримали у геодезії спеціальні назви. Рухома лінія b ₁ А₂ називається лінією візування, а прямовисна площина К ₁ - колімаційною площиною.

Кутомірний прилад, призначений для вимірювання горизонтальних і вертикальних кутів, називають теодолітом (рис.

Виходячи з принципової схеми кутових вимірювань, теодоліт має такі геометричні елементи:

- вертикальну вісь обертання (ZZ);

- вісь візування (VV);

- горизонтальну вісь обертання зорової труби (HH);

- площину горизонтального кутомірного круга (ГК);

- площину вертикального кутомірного круга (ВК).

При цьому вказані геометричні елементи повинні розміщуватися паралельно або перпендикулярно відносно іншого так, щоб це забезпечувало математичні умови принципу кутових вимірювань.

Теодоліт під час кутових вимірювань, як правило, встановлюється на штативі 1 (рис. 6.2), який складається з металевої верхньої частини - головки і трьох розсувних змінної довжини ніжок 2. Становим гвинтом З теодоліт прикріплюється до головки штатива. На гвинті є центрований гачок 4, до якого підвішується нитковий висок. За допомогою виска центрують теодоліт над вершиною вимірюваного кута.

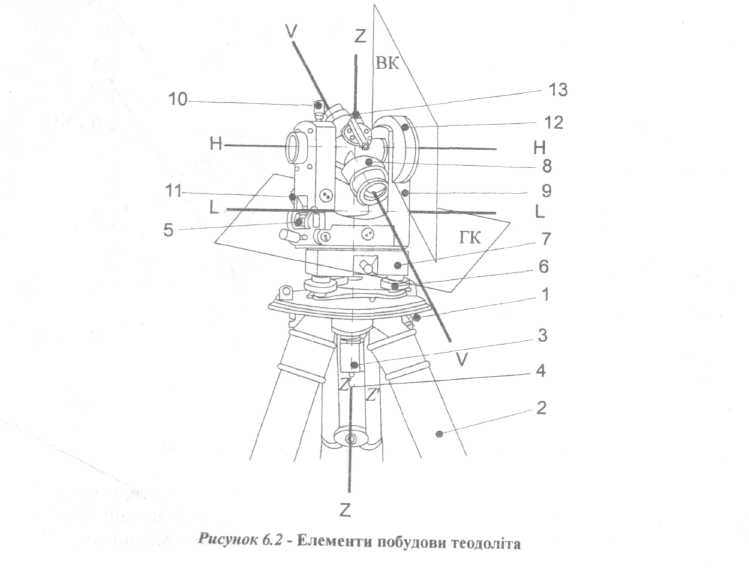Вісь обертання ZZ теодоліта встановлюється у прямовисне положення за циліндричним рівнем 5 ( LL - вісь рівня) за допомогою трьох підйомних гвинтів 6 підставки теодоліта 7 (нижня частина теодоліта). Горизонтальний кутомірний круг називається лімбом, він розміщується в площині ГК, яка стає горизонтальною при прямовисному положенні осі ZZ .

Візування на точки здійснюється зоровою трубою 8, яка обертається навколо горизонтальної осі, втулки якої розміщені в колонках 9 укріплених на алідаді. Для точного наведення і фіксування осі візування труба має закріпний 10 і навідний 11 гвинти.

Вертикальний кутомірний круг 12 розміщений у площині ВК на одному з кінців осі. Він теж складається з лімба та алідади.

При вимірюванні кута β (рис. 6.1 а) обертанням алідади теодоліта і зорової труби послідовно наводять вісь візування на точки А і С місцевості, при цьому колімаційна площина послідовно проходить через сторони ВА і ВС вимірюваного кута. При кожному суміщенні осі візування з вершиною кута беруть відліки за поділками лімба горизонтального круга за допомогою відлікового мікроскопа 13 (рис. 6.2).

Таким чином, щоб теодолітом можна було виміряти горизонтальний кут, між його геометричними осями повинні виконуватися такі основні умови:

- вісь циліндричного рівня LL повинна бути перпендикулярною до осі обертання ZZ;

- вісь візування VV повинна бути перпендикулярною до осі обертання труби НН;

- вісь обертання НН труби повинна бути перпендикулярною до осі обертання ZZ .

Дата добавления: 2019-03-09; просмотров: 1620; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!