Описание лабораторной установки

Лабораторная установка состоит из отдельного макета и двух осциллографов С1–83 (I) и С1–83 (II).

В отдельном макете находятся генератор исследуемых случайных сигналов, а также измерители функции распределения вероятностей и плотности распределения вероятностей. Структурная схема макета установки (рис. 3.9) изображена на его передней панели.

Рис. 3.9

С выхода « » осциллографа С1–83 (I) снимается в качестве опорного пилообразное напряжение горизонтальной развертки и подается в лабораторный макет на «Вход U» для использования в качестве аргумента «U» функции распределения.

Выход «Функция распределения» установки соединяется с входом «U» осциллографа С1–83 (I). На экране осциллографа появляется изображение функции распределения F(U) или плотности распределения вероятностей p(U). Выбор зависит от положения переключателя «F(U) — p(U)» на передней панели экспериментальной установки.

Выход «Форма сигнала» установки соединяется со входом «U» осциллографа С1–83 (II), на экране которого наблюдают изображение исследуемого сигнала.

В макете установки имеются следующие источники сигналов:

1. Четыре генератора гармонических колебаний различных частот.

2. Четыре генератора сигналов треугольной формы различных частот.

3. Формирователь шума с распределением по обобщенному закону Рэлея.

4. Генератор шума с гауссовским законом распределения.

Имеется также вход для внешнего сигнала.

Выходы всех источников сигналов подключены через сумматор å ко входу измерителя функций распределения. Каждый источник сигнала имеет тумблер включения и регулировку уровня (только часть регуляторов уровня выведена на переднюю панель).

Задание и указания к выполнению работы

1. Подготовить установку к измерениям. На осциллографе С1–83 (I) установить коэффициент развертки 0,1 с/дел, коэффициент отклонения 0,2 В/дел. Включить осциллографы и экспериментальную установку. В установке выключить все генераторы (ручки тумблеров — вниз), что соответствует нулевому сигналу на входе измерителя функции распределения; тумблер «Функции распределения» — в положении F(U). На экране С1–83 (I) появится изображение ступенчатой функции

Регулировкой смещения и коэффициента отклонения осциллографа установить изображение так, чтобы скачок находился в центре экрана и величина скачка была равна 3–4 см.

2. Откалибровать изображение на экране С1–83 (I). Включить генератор треугольного сигнала № 4 (ручка тумблера — вверх). На экране С1‑83 (I) переход от F(U) = 0 к F(U) = 1 будет иметь вид наклонной линии (см. рис. 3.3, в). Точки излома соответствуют минимальному и максимальному значениям треугольного сигнала. Измерить расстояние по горизонтали между точками излома — L, дел. На экране осциллографа С1‑83 (II) получить изображение треугольного сигнала (см. рис. 3.3, а) и измерить его размах , В. Масштаб по горизонтали для изображения на экране осциллографа С1–83 (I) равен 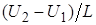, В/дел. Данный масштаб является одинаковым для всех получаемых в дальнейшем графиков функций распределения F(U) и плотностей вероятности p(U).

Переключатель «Функции распределения» в установке перевести в положение «p(U)». На экране С1–83 (I) появится П-образное изображение, соответствующее равномерному распределению вероятности, характерному для треугольного сигнала (см. рис. 3.3, б).

Если изображение по вертикали занимает DL делений, то масштаб изображения p(U) по вертикали составит 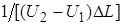, (В×дел)^–1. Данный масштаб является одинаковым для всех получаемых в дальнейшем графиков плотностей вероятности p(U).

Определять вертикальный масштаб для графиков функций распределения нет необходимости — он очевиден благодаря предельным свойствам функций распределения ( и ).

В дальнейшем коэффициент отклонения осциллографа C1–83 (I) не изменять.

3. Исследовать функции распределения и плотности вероятностей мгновенных значений для следующих сигналов:

· гармонического сигнала № 4 при двух значениях его амплитуды;

· треугольного сигнала № 4 при двух значениях его амплитуды;

· гауссовского шума при двух значениях его дисперсии;

· рэлеевского шума при нулевом и ненулевом значениях амплитуды детерминированного сигнала.

Указанные варьируемые параметры выбрать самостоятельно таким образом, чтобы на графиках было хорошо заметно их влияние на форму функции распределения и плотности вероятности.

Исследование производится следующим образом. В исходном положении все генераторы выключены. Включить генератор исследуемого сигнала. По изображению сигнала на экране С1–83 (II) убедиться, что включен требуемый сигнал. По изображению на экране С1–83 (II) или по вольтметру, подключенному к выходу «Форма сигнала» установки (параллельно входу осциллографа), определить диапазон регулировки уровня исследуемого сигнала (амплитуда для гармонического и треугольного, эффективное значение для шумов). В этом диапазоне выбрать два значения уровня исследуемого сигнала и для каждого из них зарисовать с экрана С1–83 (I) изображения функций p(U) и F(U) с учетом ранее определенных масштабов по осям.

4. Исследовать сходимость к гауссовскому закону распределения суммы независимых случайных сигналов. Выяснить, для какого из двух исходных законов распределения — равномерного (треугольный сигнал) или вида (гармонический сигнал) — характерна более быстрая сходимость.

Для суммы гармонических сигналов исследование производится следующим образом. В исходном положении все генераторы выключены. Включить генератор синусоидального сигнала № 1 и зарисовать график функции распределения F(U). Затем, не выключая генератор этого сигнала, включить генератор синусоидального сигнала № 2 и зарисовать график функции распределения F(U) для суммы двух синусоидальных сигналов. Далее поочередно дополнительно включить генераторы синусоидальных сигналов № 3 и № 4, каждый раз зарисовывая графики функции распределения суммарного сигнала.

Для суммы треугольных сигналов исследование производится аналогичным образом.

Содержание отчета

Отчет по работе должен включать в себя следующее:

· результаты определения масштабов графиков согласно п. 2;

· графики функций распределения и плотностей вероятностей значений сигналов, исследованных в п. 3.

· анализ соответствия графиков, полученных в п. 3, теоретическим результатам (выражения (3.3)–(3.7)) [4];

· графики функций распределения для последовательных сумм синусоидальных и треугольных сигналов согласно п. 4;

· вывод о скорости сходимости распределения вероятности суммы независимых случайных сигналов к гауссовскому закону.

Контрольные вопросы

1. Как измеряют функцию распределения по одной реализации эргодического случайного процесса?

2. Определить функцию распределения F(x), математическое ожидание m_x и дисперсию D_x для случайной величины, имеющей заданную преподавателем плотность вероятности p(x).

3. Определить плотность вероятности p(x), математическое ожидание m_x и дисперсию D_x для случайной величины, имеющей заданную преподавателем функцию распределения F(x).

4. Могут ли эти функции быть функциями распределения вероятности?

а б в

5. Могут ли эти функции быть функциями плотности вероятности?

а б в

6. Как зависит плотность вероятности нормального закона от входящих в нее параметров? Пояснить графически.

7. Как зависит плотность вероятности обобщенного закона Рэлея от параметров и s?

8. Плотность распределения случайного сигнала u(t) представлена суммой

Записать и построить функцию распределения F(u) и определить математическое ожидание и дисперсию u(t). Привести пример реализации u(t).

9. Известно, что плотность распределения суммы двух независимых случайных сигналов u(t) и v(t) с плотностями распределения и является сверткой

Рассчитать для заданной преподавателем суммы двух сигналов, исследованных в работе, и сравнить с экспериментальными данными.

10. Случайная величина j принимает значения p/4 и –p/4 с вероятностями 0,5. Найти ковариационную функцию случайного процесса x(t) = sin(w₀t + j). Является ли данный процесс стационарным?

11. Случайный процесс x_i(t) = 2sin(w₀t + j_i), где {j_i} — набор статистически независимых случайных величин, равномерно распределенных в диапазоне от –p до p. Найти плотность вероятности случайного процесса .

12. Может ли функция распределения вероятности:

а) принимать постоянное значение на некотором интервале?

б) иметь скачок в некоторой точке?

Если может, то что можно сказать о данном интервале (точке)?

4. ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК
ЧАСТОТНО-ИЗБИРАТЕЛЬНЫХ ЦЕПЕЙ
НА ОСНОВЕ КОЛЕБАТЕЛЬНЫХ КОНТУРОВ

Цель работы — изучение частотно-избирательных цепей на основе колебательных контуров. Последовательный и параллельный колебательные контуры часто используются в качестве основного элемента линейных частотно-избирательных цепей (фильтров, резонансных усилителей и т. п.). К основным характеристикам линейных цепей относятся импульсная характеристика h(t)и комплексный коэффициент передачи (частотная характеристика) . В исследуемых цепях вид этих характеристик полностью определяется резонансной частотой и добротностью Q контуров, а связь между ними — преобразованиями Фурье.

Исследуются временные и частотные характеристики колебательных контуров, влияние на них активных потерь, взаимосвязь временных и частотных параметров контуров.

Теоретические сведения

Последовательный колебательный контур(рис. 4.1, а) удобно рассматривать как четырехполюсник. На резонансной частоте он обладает низким входным сопротивлением и для обеспечения колебательного режима должен подключаться к источнику сигнала с достаточно малым выходным сопротивлением , таким, чтобы выполнялось условие , где — волновое, или характеристическое сопротивление контура.

а б
Рис. 4.1

Пренебрегая сопротивлением нагрузки (полагая его достаточно большим, >> r), запишем дифференциальное уравнение для выходного напряжения четырехполюсника :

, (4.1)

где в качестве входного воздействия взята взвешенная функция включения (функция Хевисайда). Однородному дифференциальному уравнению

(4.2)

соответствует характеристическое уравнение

с корнями ; здесь a = r/(2L), («собственная» резонансная частота контура). Решение неоднородного дифференциального уравнения (4.1) ищут в виде суммы решения уравнения (4.2) и так называемого частного решения уравнения (4.1), которое при выбранном входном воздействии оказывается просто константой U:

Используя очевидные начальные условия 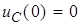, i(0) = 0, находят константы и и записывают решение

которое при нормировке к U = 1 В становится безразмерной переходной характеристикой четырехполюсника g(t). Так как импульсная характеристика h(t) = dg/dt, получают

, t ³ 0. (4.3)

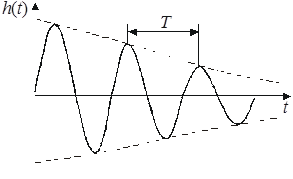
График h(t) приведен на рис. 4.1, б. В выражении (4.3) приближение сделано в предположении малых потерь, 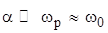, а также введена постоянная времени последовательного колебательного контура. Здесь — нагруженная добротность контура, определяемая соотношением

. (4.4)

Комплексный коэффициент передачи последовательного колебательного контура в так называемом приближении малых расстроек рассчитывается просто:

= . (4.5)

Здесь принято , — в приближении малых расстроек.

Комплексный коэффициент передачи может быть также получен в результате применения к импульсной характеристике h(t) прямого преобразования Фурье

. (4.6)

Нижним пределом интеграла в выражении (4.6) берут 0, так как импульсная характеристика физически реализуемого четырехполюсника существует только при t ³ 0. С использованием введенной постоянной времени 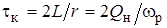результат (4.5) записывается в виде

АЧХ и ФЧХ цепи определяются выражениями

, . (4.7)

Входное сопротивление последовательного колебательного контура на резонансной частоте мало и равно эквивалентному сопротивлению потерь, = r. Поэтому последовательные контуры часто используют как режекторные фильтры для подавления сигнала на резонансной частоте.

Параллельный колебательный контур представляет собой параллельное соединение L и C элементов (рис. 4.2, а). Используют высокодобротные катушки индуктивности и конденсаторы с малыми потерями, причем потерями в конденсаторе в большинстве случаев пренебрегают и собственные потери контура представляют сопротивлением , отнесенным к индуктивности. Для удобства анализа схемы последовательное соединение и L пересчитывают в параллельное соединение эквивалентного сопротивления и L, пренебрегая квадратом сопротивления потерь по сравнению с квадратом индуктивного сопротивления, ( L)² >> . На резонансной частоте параллельный контур имеет достаточно высокое эквивалентное сопротивление , где r, как и для последовательного контура — волновое или характеристическое сопротивление, равное сопротивлению одной ветви контура на резонансной частоте, ; 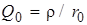— собственная (ненагруженная) добротность колебательной системы. Для сохранения в контуре колебательного режима добротность должна быть достаточно велика, следовательно, подключаемые к нему сопротивления источника сигнала (генератора) и нагрузки должны быть большими ( , ³ ).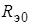

а б
Рис. 4.2

Для исследования временных характеристик параллельного контура источник напряжения u(t) (рис. 4.2, а) заменяют источником тока , а параллельно подключенные к контуру сопротивления и пересчитывают с учетом в эквивалентное сопротивление (рис. 4.2, б) в соответствии с равенством , где , — нагруженная добротность параллельного контура. Иногда используют понятие внешней добротности , которая связывает собственную и нагруженную добротности .

Импульсной реакцией или импульсной характеристикой параллельного колебательного контура принято называть напряжение при воздействии на контур дельта-импульса тока (при экспериментальном определении импульсной характеристики используют достаточно короткий импульс). Импульсная реакция параллельного контура имеет колебательный характер и может быть записана как

. (4.8)

Здесь . Приближение (4.8) с учетом того, что 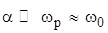(напомним, что , где 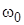— «собственная» резонансная частота контура), принимают для высокодобротного контура. Вводят также понятие постоянной времени нагруженного параллельного контура и записывают выражение (4.8) в форме

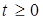, . (4.9)

Из выражений (4.3) и (4.9) следует, что 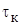является интервалом времени между точками, соответствующими спаду огибающей импульсной характеристики в e = 2,72… (основание натуральных логарифмов) раз.

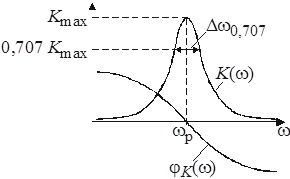
а б
Рис. 4.3

Из выражения (4.6) следует, что при безразмерном размерностью h(t) является 1/с. При определении импульсной характеристики параллельного колебательного контура было принято воздействие в виде дельта-импульса тока, а в качестве реакции — напряжение на контуре, поэтому размерностью здесь будет Ом — размерность отношения , — а размерностью h(t) будет Ом/с = 1/Ф, что поясняет присутствие в выражениях (4.8) и (4.9) множителя 1/С. Комплексный коэффициент передачи параллельного колебательного контура записывается как

, (4.10)

где — абсолютная расстройка, как и для последовательного колебательного контура. Можно показать, что если — полоса заграждения контура на уровне 0,707 от максимума АЧХ, то 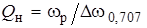— добротность контура, практически совпадающая с нагруженной добротностью контура, определенной через временные характеристики. Из выражения (4.10) определяют АЧХ и ФЧХ цепи (рис. 4.3, б)

, . (4.11)

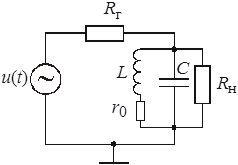
Рис. 4.4

Снизить влияние сопротивлений и на колебательный контур можно, используя так называемое частичное включение контура: генератор и нагрузка подключаются к отводу катушки индуктивности и к части емкостной ветви (рис. 4.4) контура. Используют коэффициенты включения

, .

При подключении источника напряжения u(t) к части индуктивной ветви контура он может быть заменен генератором тока , подключенным к контуру вида рис. 4.2, б. В этом случае комплексная частотная характеристика приобретает вид

где — эквивалентная нагруженная добротность, — эквивалентное сопротивление контура с учетом собственных и внешних потерь, — собственные потери контура (от коэффициентов включения не зависят), , — пересчитанные с учетом частичного включения сопротивления генератора и нагрузки. Подбором коэффициентов включения удается обеспечить требуемую полосу пропускания контура и расчетное эквивалентное сопротивление. Это особенно важно при использовании параллельного контура в качестве нагрузки в резонансных усилителях и генераторах.

Дата добавления: 2019-03-09; просмотров: 254; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!