Is he writing a test? – No, he isn’t.
Are you writing now? – Yes,I am.
A Underline the correct form.
| I | A: I 1)think/am thinking about visiting Vlad this afternoon. B: I wouldn’t bother. I 2)think/am thinking he’s away on holiday. |
| II | A: Mr Ivanov 3) has/is having a telephone message from his wife. B: Can it wait? He 4) has/is having a business meeting and I don’t want to disturb him. |
| III | A: Maxim 5) is/is being usually rude, but today he 6) is/is being polite to his colleagues. |
| IV | Julie 7)is/is being usually patient, but to day she 8) is/is being impatient. |
| V | As a rule David 9) cooks/is cooking some soup for dinner. |
| VI | She 10) meets/is meeting Kate in the Yalta office on Monday. |
B Put the verbs in brackets into the Present Simple or Present Continuous.
Son: Hello Dad, I am near Drama Theatre. It 1(pour) _____ with rain, and I
2 (not/have got) any money.
Dad: What 3 (you/want) _____ me to do about it?
Son: Could you come and pick me up?
Dad: You 4 (always/ask). I 5 (feel/tired)_____ after my work.
Son: Please, Dad. I am tired and hungry. My evening classes 6 (start) _____at 7.00 and I have to be there on time. Can’t Mum come and get me?
Dad: The Ivanovs 7 (visit) _____ us tonight and she is busy in the kitchen. She 8 (bake)_____ a cake at the moment.
Son: Please, Dad. I 9 (ask) you to do this for me one last time. My mark actually 10 (depend) on you. I must come on time to give my presentation in class.
Dad: OK. I’ll be there in half an hour. But this is the last time. I 11 (mean) it!
Speaking
Find a partner from the other group. Tell each other the information you read about one of the universities.
Imagine you meet someone from Nigeria who wants to study at Donetsk National University. Tell him/her about your university and be ready to answer the questions about it.
Learn mathematics in English
Read the text and do the following tasks.
Fractions
5; 241; 74 are whole numbers or integers.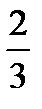 
; 
; 0.5; 0.102 are fractions. A fraction (from the Latin fractus, broken) is a number that represents part of a whole. The earliest fractions were reciprocals of integers: ancient symbols representing one part of two, one part of three, one part of four, and so on. A much later development were the common or vulgar fractions which are still used today (½, ⅝, ¾, etc.) and which consist of a numerator and a denominator, the numerator representing a number of equal parts and the denominator telling how many of those parts make up a whole. An example is 
, in which the numerator, 3, tells us that the fraction represents 3 equal parts, and the denominator, 4, tells us that 4 parts make up a whole.
|
|
|
A still later development was the fraction, now called simply a decimal, in which the denominator is a power of ten, determined by the number of digits to the right of a decimal separator, the appearance of which (e.g., a period, a raised period (•), a comma) depends on the locale). Thus for 0.75 the numerator is 75 and the denominator is 10 to the second power, i.e. 100, because there are two digits to the right of the decimal point. If 100 is divided by 3, the quotient is 33.33. In spoken English it is, ‘Thirty - three point three, three recurring’. If 100 is divided by 3, and the quotient is written 33.333, it is correct to three significant figures. If the quotient is written 33.33 it is correct to two significant figures.
A third kind of fraction still in common use is the percent age, in which the denominator is always 100. Thus 75 % (read as ‘seventy five percent’) means 
.
Other uses of fractions are to represent ratios, and to represent division. Thus the fraction 
is also used to represent the ratio 3:4 (three to four) and the division 3 ÷ 4 (three divided by four).
In mathematics, the set of all common (vulgar) fractions is called the set of rational numbers, and is represented by the symbol Q.
Common (vulgar) fractions
A common fraction (or vulgarfraction) is a rational number written as one integer (the numerator) divided by another non-zero integer (the denominator) such as 
.
A common fraction is said to be a proper fraction if the absolute value of the numerator is less than the absolute value of the denominator, that is, if the absolute value of the entire fraction is less than 1; a common fraction is said to be an improper fraction if the absolute value of the numerator is greater than or equal to the absolute value of the denominator (e.g. 
).
|
|
|
In pairs, look at the highlighted words and phrases. Try to guess what they mean from the context. Then check with your dictionary or teacher. Work out the list of the terms involved, make a kind of glossary.
Дата добавления: 2019-02-26; просмотров: 266; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!