Теорема Гаусса для электростатического поля в вакууме. Определение напряженности поля точечного заряда с помощью теоремы Гаусса.

⇐ ПредыдущаяСтр 10 из 15Следующая ⇒

Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀. Согласно закону Кулона, напряженность электрического поля в точке на поверхности сферы равна Е = (1/4πε₀)(Q/r)

Тогда теорема гаусса для частного случая точечного заряда в центре сферической поверхности: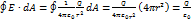

26. Теорема Гаусса для электростатического поля. Расчет напряженности поля равномерно заряженной сферы радиуса R с известной поверхностной плотностью заряда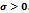

Найдем поток вектора Е сквозь сферическую поверхность S, в центре которой находится точечный заряд q.

В этом случае dФ_E=EdS, т.к. направления Е и n во всех точках сферической поверхности совпадают. С учетом напряженности поля точечного заряда E= 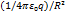и того, что площадь поверхности сферы 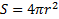получим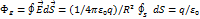

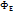- алгебраическая величина, зависящая от знака заряда. Например, при q<0 линии Е направлены к заряду и противоположны направлению внешней нормали n. Поэтому в таком случае поток отрицателен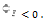

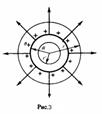Пусть замкнутая поверхность S1 вокруг заряда q имеет произвольную форму. Очевидно, что поверхность S1 пересекается тем же числом линий Е, что и поверхность S. Следовательно, поток вектора Е сквозь произвольную поверхность S1 также определяется полученной формулой .

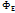Если заряд будет находиться вне замкнутой поверхности, то, очевидно, сколько линий войдет в замкнутую область, столько же из нее и выйдет. В результате поток вектора Е будет равен нулю.

Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +σ. Т.к. заряд распределен равномерно поверхности то поле, которое создаётся им, обладает сферической симметрией. Значит линии напряженности направлены радиально. Проведем мысленно сферу радиуса r, которая имеет общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, который создает рассматриваемое поле, и, по теореме Гаусса, 4πr²E = Q/ε₀ , откуда E= 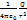. При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда.

27. Теорема Гаусса для электростатического поля. Расчет поля бесконечного прямолинейного провода, заряженного с линейной плотностью заряда .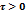

Теорема Гаусса см. вопрос 26!

Бесконечная равномерно заряженная нить

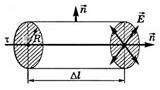
Пусть τ — линейная плотность заряда нити. Выделим участок нити длиной Δl и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью.

Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность N=E⋅2πRΔl N=E⋅2πRΔl, где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный поток напряженности через выделенный цилиндр

N=E⋅2πRΔl. N=E⋅2πRΔl.

Заряд, находящийся внутри этого цилиндра, q = τ · Δl. Согласно теореме Остроградского—Гаусса, можно записать E⋅2πRΔl=τΔlε0ε E⋅2πRΔl=τΔlε0ε . Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее, E=τ2πε0εR.

28. Теорема Гаусса для электростатического поля в вакууме. Расчет поля равномерно заряженного по объему шара с известной объемной плотностью заряда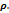

Теорема Гаусса для электростатического поля в вакууме см. вопрос 25!

Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ=dQ/dV — заряд, приходящийся на единицу объема). Учитывая соображения симметрии, можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае: E= 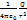. Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q’=4/3πr’³ρ.

Поэтому, согласно теореме Гаусса, 4πr’²E=Q’/ε₀=4/3πr³ρ/ε₀. Учитывая, что ρ=Q/(4/3πR³)

получим: E= 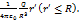Таким образом, напряженность ноля вне равномерно заряженного шара описывается формулой: E= 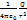, а внутри его изменяется линейно с расстоянием r' согласно выражению. График зависимости E от r:

Дата добавления: 2019-02-22; просмотров: 458; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!