Деформирование окружающих скважину горных пород после вскрытия их бурением
Аналитическое решение об упругом деформировании горных пород по-сле вскрытия их скважиной и соответствующем изменении размера сечения ствола вертикальной скважины рассмотрим при допущении о плоской деформации горных пород, окружающих скважину, т.е. изменение деформации в направлении, параллельном оси скважины, равно нулю. Задача решается в цилиндрической системе координат z-R, в которой аппликата z вертикальна и совпадает с осью скважины. Расчетная схема приведена на рисунке 4.59.
Горная порода вскрыта скважиной радиусом Rc, в которой находится буровой раствор, создающий на стенки скважины давление, равное р с. За счет разности давлений рс и рб произошло перемещение горной породы в радиальном направлении на величину u, которое в конечном счете привело к смещению стенки скважиеы на величину Rc.
| Дифференциальное уравнение, описывающее деформацию малого элемен- | |||||||
| та в перемещениях, имеет вид | |||||||
| d 2u | + | du | − | u | = 0 , | (4.125) | |
| dR2 | R ⋅ dR | R2 | |||||
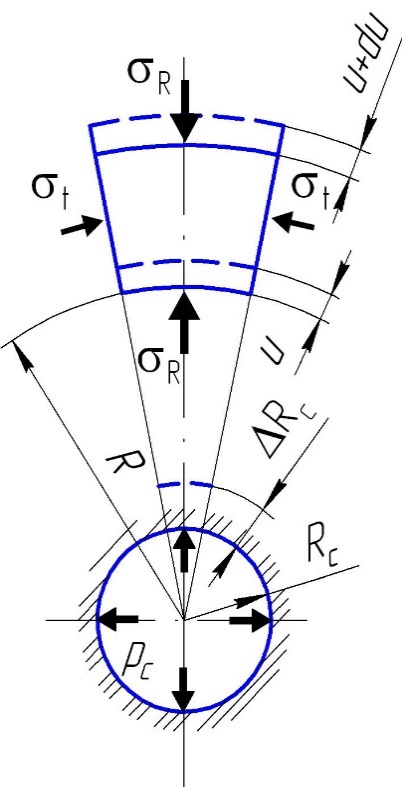
Рис. 4.59. Схема к расчету смещения стенки скважины
где u – перемещение внутренней поверхности малого элемента после вскрытия горной породы скважиной; R – расстояние от начала координат (текущий радиус). Для решения уравнения следует перейти к новой переменной
t = lnR .
После необходимых преобразований, получим следующее решение уравнения (4.125):
|
|
|
u = C1 + C2 /R, (4.126)
где С1 и С2 – постоянные интегрирования, величины которых найдем из граничных условий:
при R = ∞ горная порода находится в естественном напряженном состоянии, т.е. σR = σt = рб, u = 0;
при R = Rc радиальные напряжения на стенке скважины σR = рс; u = DRc.
Из первого граничного условия следует, что С1 = 0.
Для определения величины C2 воспользуемся вторым граничным условием и зависимостью σR от R (4.27). До вскрытия скважиной радиальное напряжение на поверхности будущей стенки скважины такое же, как и в окружающем массиве горных пород, т.е. σR = рб, а u = DRc = 0. После вскрытия скважиной напряжение на стенке изменится и станет равным рс. Уравнение равновесия для стенки скважины примет вид
рб – рс =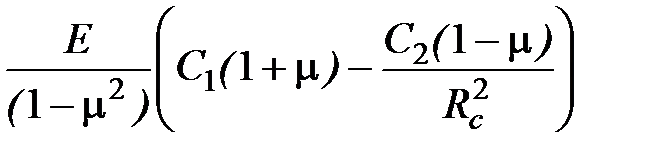 
, (4.127)
где Е –модуль Юнга,определяемый для горных пород при испытании на одноосное сжатие. Отношение
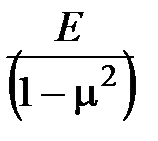= С (4.128)
известно как модуль деформации (упругости) горной породы при вдавливании инденторов и определяется при испытании горных пород методом статического вдавливания штампа. Тогда с учетом (4.128) и то, что С1 = 0, изменение радиального напряжения на стенке скважины принимает вид
|
|
|
рс – рб =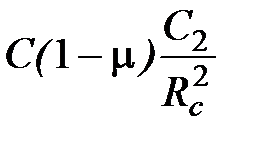 
,
из которого следует, что
C2 =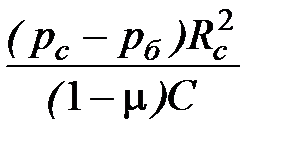 
. (4.129)
Подставив (4.129) в выражение (4.126) с учетом, что u = DRc, получим формулу для расчета смещения DRc стенки вертикальной скважины:
DRc =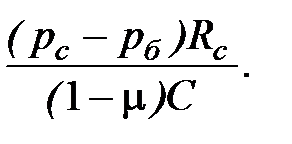 
(4.130)
Из формулы (4.130) следует, что при рс > рб скважина деформируется с увеличением радиуса, а при рс < рб – с уменьшением радиуса. Упругие характеристики горной породы влияют по-разному: с увеличением коэффициента Пуассона смещение стенок возрастает, а с увеличением модуля деформации – снижается.
Большие значения μ и малые значения модуля С характерны для мягких пород и пород средней твердости. Поэтому именно в таких горных породах следует ожидать осложнений, связанных со смещением стенок скважины.
Решение методом численного итегрирования обусловлено тем,напряженное состояние и деформирование наклонной скважины неосесимметрично и точного решения о смещении ее стенок нет. Поэтому был использован метод численного интегрирования.
Из формул С. Г. Лехницкого следует, что компоненты напряжений в горной породе по мере удаления от стенки скважины стремятся к величине естественных напряжений, как к асимптоте, и на расстоянии около 10Rc отличаются от них не более, чем на 1 %. Это дало основание ограничить зону влияния вокруг скважины некоторым контуром радиусом Rк и применить численное интегрирование для расчета величины Rc в общем случае.
|
|
|
На контуре и далее принимаем, что радиальное и тангенциальное напряжения равны естественному боковому давлению горной породы, а перемещение горной породы под влиянием скважины равно нулю.
Обоснование параметров численного интегрирования выполнено на примере вертикальной скважины, т.к. полученная формула (4.130) позволяет вычислить ошибку приближенного решения. Расчетная схема для вертикальной скважины приведена на рисунке 4.60.
Внутри контура изменение размеров выделенного элемента обусловлено изменениями компонент напряжений по сравнению с напряжениями на контуре. В соответствии с законом Гука радиальная деформация выделенного элемента равна
DR = εRh = (μ(Dst + Dsz) – DsR)/E, (4.131)
где DsR = рб – sR; Dst = рб – st.
Из условия εz = 0 (плоская деформация) следует, что
Dsz = μ(Dst + DsR). (4.132)
|
|
|
Подставив выражение (4.132) в формулу (4.131) и сделав преобразования, получим
DR = h(((μ/(1 – μ))Dst ) – DsR)(1 – μ2)/E. (4.133)
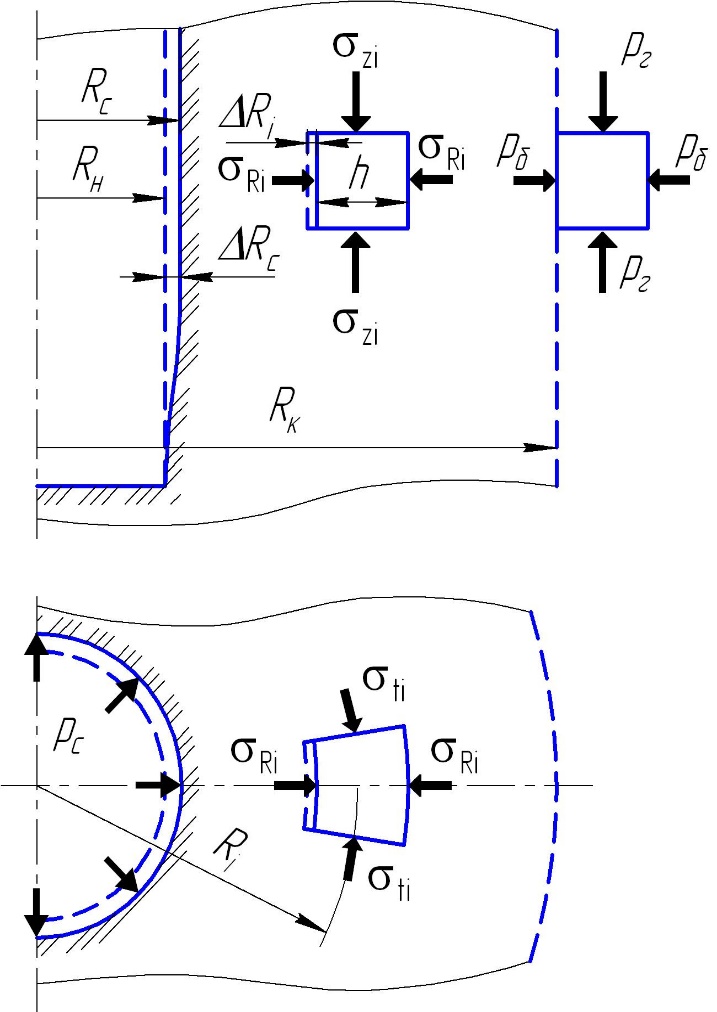
Рис. 4.60. Схема деформирования вертикальной скважины
Величина μ/(1 – μ) = λу, т.е. соответствует упругой величине коэффициента бокового распора горной породы, а величина Е/(1 – μ2) = С и соответствует модулю упругости горной породы при вдавливании. Тогда с учетом сказанного выше формула (4.131) для i-го элемента принимает вид
DRi =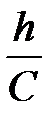 
(λу· Dsti – DsRi). (4.134)
Величины DsRi и Dsti для вертикальной скважины определим, использовав формулы С. Г. Лехницкого:
DsRi = sRi – λрг = (pc – λрг) 
; (4.135)
Dsti = sti – λрг = -( pc – λрг)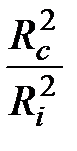 
(4.136)
Для удобства элементу на контуре присваиваем индекс 1, а на стенке скважины – индекс п. Тогда средний радиус i -го элемента определим по формуле
Ri = R к( i -1) +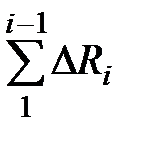 
– h / 2, (4.137)
где R к i –- радиус контура i -го элемента; DRi – радиальная деформация i -го элемента. Сумма смещений внутренних поверхностей элементов равна смещению стенки скважины, т.е.
DRc =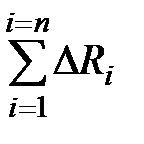 
. (4.138)
Величину ошибки D расчета смещения стенки по формуле (4.138) от рассчитанного по формуле (4.130) определим по формуле
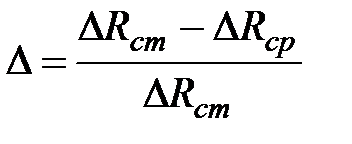100 %, (4.139)
где DR ст – смещение теоретическое, рассчитанное по формуле (4.130); DR ср – смещение, рассчитанное по формуле 94.138).
Расчеты показали, что основное влияние на ошибку определения смещения стенки скважины оказывает величина радиуса контура, тогда как толщина элемента влияет весьма слабо.
Решение о смещении стенки наклонной скважины является общим длярассматриваемой задачи. Напряженное состояние наклонной и горизонтальной скважин неосесимметрично, поэтому в результате деформирования сечение ствола скважины приобретает форму, близкую к эллипсу. Это утверждение подтверждается просмотром кавернограмм наклонных скважин, записанных каверномером в двух взаимно перпендикулярных направлениях. Пример такой записи приведен на рисунке 4.61. Из рисунка видно, что размеры скважины в двух взаимно перпендикулярных направлениях существенно отличаются. При этом радиус скважины может быть как больше, так и меньше номинального. Измеренные радиусы скважины фактически представляют собой величины полуосей эллиптического сечения скважины.
Расчетная схема для определения смещения стенок наклонной скважины приведена на рисунке 4.62. При бурении долото формирует круглую скважину радиусом Rн, но по мере удаления долота от зафиксированного поперечного сечения ствола скважины происходит его деформирование, как показано в сечении I-I.
Рис. 4.61. Кавернограмма интервала скважины с углом искривления 54°: ряд 1 – номинальный радиус скважины; ряды 2 и 3 – измеренные радиусы скважины
В горизонтальном направлении (линия АD) происходит смещение точки А и,соответственно,боковой стенки скважины в сторону увеличения радиусаскважины (положительное смещение), а в направлении ВЕ происходит смещение точки В и, соответственно, верхней стенки скважины к оси скважины (отрицательное смещение). Отсюда следует, что характерными являются точки А на боковой стенке и В на верхней стенке, расчет смещения которых позволяет определить большую и малую оси эллиптического сечения скважины в результате неосесимметричной деформации.
В основу расчета изменения компонент напряжений положены формулы (4.103) и (4.104) для горизонтальной скважины, также выполненные при допущении о плоской деформации горной породы после вскрытия ее скважиной. Из схемы на рисунке 4.62 видно, что на линии AD, лежащей в гори-зонтальной плоскости и проходящей через точку А перпендикулярно оси скважины , на контуре радиальное напряжение равно боковому давлению (рб = λр г), а тангенциальное – давлению рα.
На линии BE, проходящей через точку В и лежащей в вертикальной плоскости, проходящей через ось скважины , радиальное напряжение равно давлению рα, а тангенциальное – боковому рб. Величина рα равна
| рα = рг·sin2α+ pб·соs2α. | (4.140) |
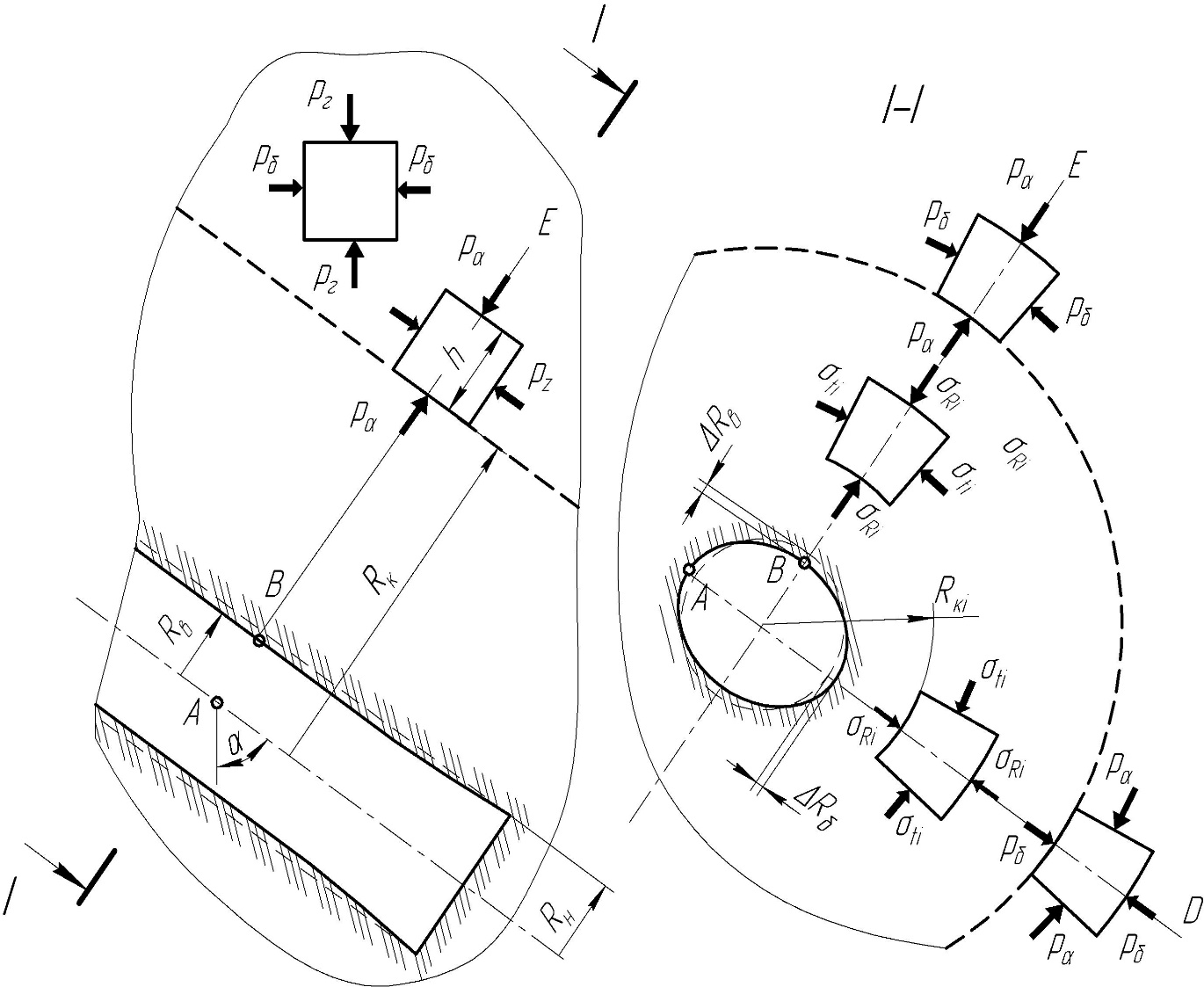
Рис. 4.62. Схема к расчету смещения стенок наклонной скважины
В таком виде расчетная схема аналогична расчетной схеме для горизонтальной скважины. После необходимых преобразований формулы для расчета изменения компонент напряжений за боковой стенкой наклонной скважины по линии AD внутри контура приняли вид:
DsRбi =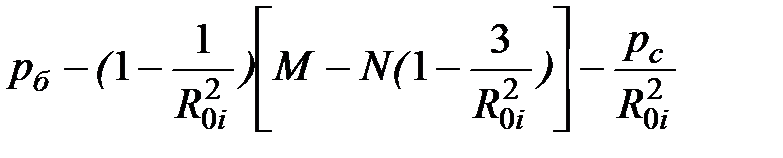 
; (4.141)
Dstбi =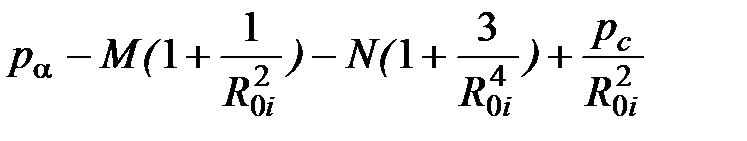 
, (4.142)
где R0i = Ri / Rн; М = (рα + рб)/2; N = (рα – рб)/2.
А формулы для расчета изменения компонент напряжений над верхней стенкой наклонной скважины по линии BE внутри контура приняли вид:
DsRвi =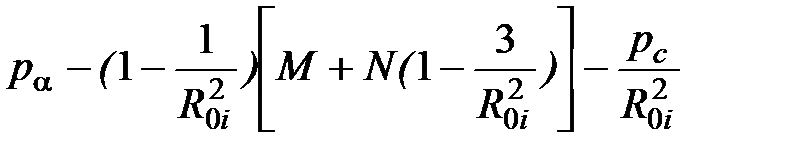 
; (4.143) Dstвi = 
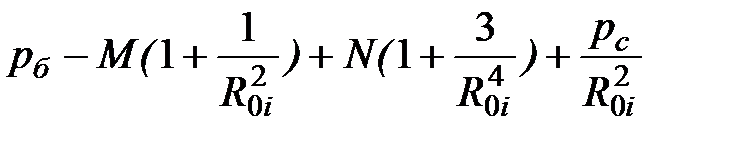. (4.144)
Последовательность вычислений та же, что и для вертикальной скважины, но отдельно для боковой и верхней стенок скважины. Подстановкой в формулы (4.134) и далее в (4.138) определим искомые величины смещения стенок скважины.
Вычисления могут быть выполнены в среде Excel. В таблице 4.15 приведен фрагмент такого вычисления с примером расчета для реального интервала скважины с углом искривления 70°.
Исходными данными являются геостатическое давление рг, угол искрив-ления скважины α, коэффициент Пуассона μ, фактический коэффициент бокового распора λ (в рассматриваемом примере λ = λу), модуль упругости при вдавливании С (с учетом масштабного эффекта), номинальный радиус сква-жины Rн в соответствии с радиусом долота (в рассматриваемом примере ради-ус долота диаметром 215,9 мм), относительный радиус контура Rко, равный Rк/ Rн,и относительная величина ho выделенного элемента,равная h/Rн.Реко-мендуемые величины Rко = 100, ho = 0,10. Остальные характеристики рассчи-тываются автоматически.
Из таблицы 4.15 видно, что расчет составил 990 строк (большая часть таблицы скрыта). Результат расчета выписывается из строки Rкi = Rн. В рассматриваемом примере боковая стенка (т. А) сместится в сторону увеличения размера на величину 0,30 мм, а вертикальная стенка (т. В) сместится в сторону уменьшения размера скважины на 3,1 мм.
При подстановке α = 0 получим результаты для вертикальной скважины, а при подстановке α = 90° – для горизонтальной скважины. Изменение поперечных размеров сечения скважины может привести к заклиниванию породоразрушающего инструмента при его подъеме из скважины.
Дата добавления: 2019-02-22; просмотров: 335; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!