Особенности напряженного состояния стенок горизонтальной скважины
Напряженное состояние горных пород, вскрытых горизонтальной скважиной, в отличие от вскрытых вертикальной скважиной не осесимметричное. Схема к описанию напряженного состояния горной породы вокруг горизонтальной скважины приведена на рисунке 4.55.
Решение о распределении напряжений в монолитной изотропной горной породе, окружающей горизонтальную цилиндрическую горную выработку при отсутствии в ней давления, приведено в книге И. А. Турчанинова. Ниже это решение положено в основу описания напряженного состояния горной породы вокруг горизонтальной скважины в цилиндрической системе координат.
Аппликата z совпадает с осью скважины. Компоненты напряжений σr , σt и σz являются функциями естественных напряжений – вертикального σ3, горизонтального σ1 и пластового давления рп , а также связанных со скважиной параметров – давления бурового раствора рс в скважине, полярных радиуса r угла φ.
В общем виде решение о величинах σr и σt имеет вид
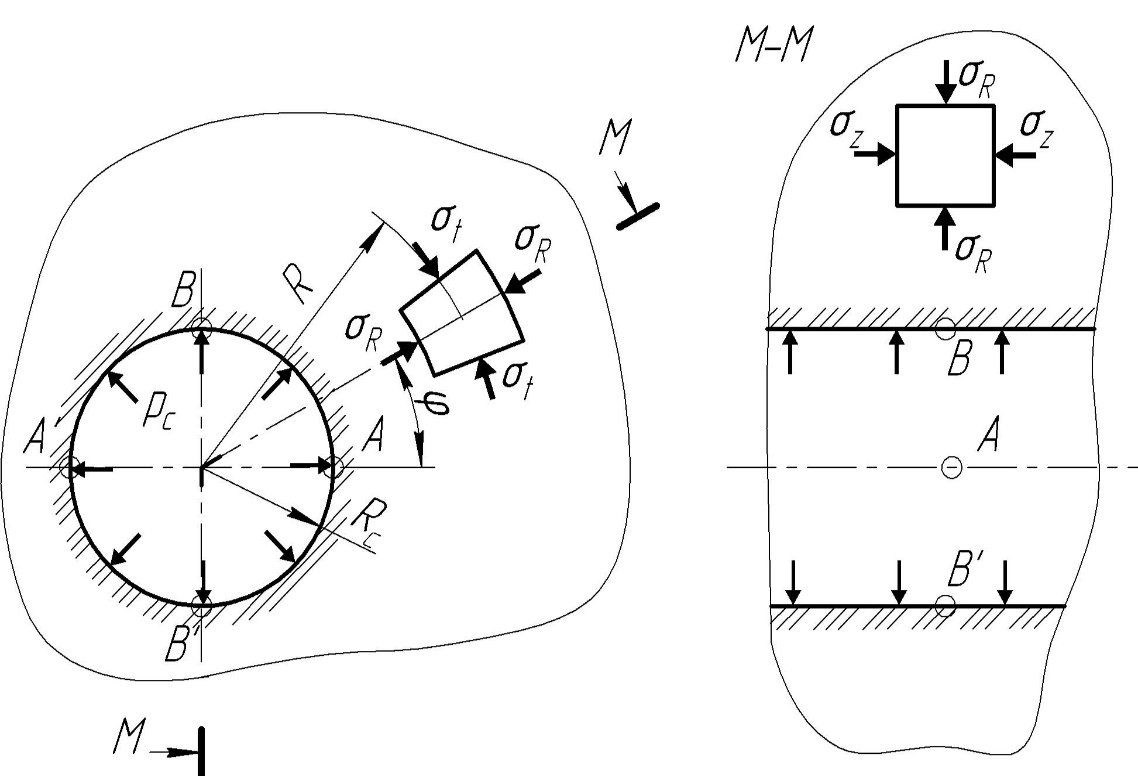
Рис. 4.55. Компоненты напряжений вокруг горизонтальной скважины
sr =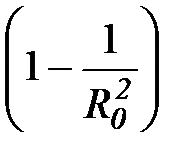 
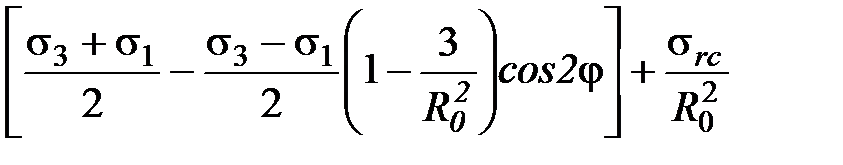; (4.103)
st = 
, (4.104)
где R0 = R /Rc – относительный полярный радиус (Rc – радиус скважины). Величины σ3 = рг, а σ1 = рб в случае монолитной горной породы или определяются по формулам (4.37) и (4.38) в случае пористой горной породы.
Компонента σz определяется из условия невозможности деформирования горных пород в направлении оси z, т . е. после вскрытия скважиной Δεz = 0. Отсюда в соответствии с обобщенным законом Гука
|
|
|
| σz = σ1 + μ(Δσr + Δσt), | (4.105) |
где μ – коэффициент Пуассона; Δσr и Δσt – приращения соответствующих компонент напряжений в горной породе после вскрытия их скважиной. Анализ напряженного состояния горных пород с использованием формул (4.103) – (4.105) показал, что , как и в случае вертикальной скважины, касательные напряжения принимают максимальные значения на стенках скважины, т.е. при R0 = 1.
На рисунке 4.56 показана зависимость компонент относительных напряжений от полярного угла φ на одной четверти окружности стенки скважины при трех значениях коэффициента бокового распора λ. Расчет компонент выполнен при следующих исходных данных: R0 = 1; рг = 2,4; рс =1,05; т = 0 (здесь т – коэффициент общей пористости). Из рисунка видно, что наиболее сильно зависит от угла φ тангенциальное напряжение σt, в меньшей степени – продольное напряжение σz, а радиальное напряжение σr от угла φ не зависит. Последнее очевидно, так как радиальные напряжения в стенке при R0 = 1 зависят только от давления промывочной жидкости в скважине и пористости горной породы. По мере увеличения угла φ от 0 до 90° наблюдается уменьшение величин напряжений σt и σz. При малых значениях коэффициента бокового распора тангенциальные напряжения при подходе к вертикальному положению меняют знак, т.е. на верхней и нижней стенках (в т. В и В', см. рис. 4.55) тангенциальные напряжения становятся растягивающими. Максимальные касательные напряжения равны полуразности тангенциальных и радиальных напряжений при φ = 0 (в точках В). Касательные напряжения в точках А (φ = 90°) существенно меньше, но в этих точках нормальные напряжения могут быть растягивающими. Поэтому в качестве экстремальных рассматриваются как точки В, так и точки А.
|
|
|
Рис. 4.54. Распределение относительных нормальных напряжений стенке горизонтальной скважины при λ = 0,11 (а), λ = 0,33 (б)
λ = 0,82 (в)
Такое распределение напряжений в стенках горизонтальной скважины позволяет определять расчетные напряжения только в т. А при φ = 0:
σr = σRс;
σt = σ3 + σ1 + 2(σ3 – σ1) – σRс; (4.106) σz = σ1 + 2μ(σ 3 – σ 1)
и в т. В при φ = 90°:
σR = σRс;
σt = σ3 + σ1 – 2(σ3 – σ1) – σRс; (4.107) σ z = σ1 – 2μ(σ 3 – σ1),
так как при других значениях полярного угла компоненты напряжений принимают промежуточные значения.
|
|
|
Дата добавления: 2019-02-22; просмотров: 416; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!