Деформирование и разрушение стенок скважины
Напряженное состояние и особенности разрушения стенок вертикальной скважины
Задача о распределении упругих напряжений в горных породах, вскрытых вертикальной скважиной, осесимметрична относительно ее оси z. Расчетная схема приведена на рисунке 4.49. Условие равновесия выделенного элемента описывается дифференциальным уравнением
| σ | r | − σ | t | + r | dσr | = 0, | (4.86) | |
| dr | ||||||||
где σr и σt – радиальные и тангенциальные нормальные напряжения соответственно; r – текущий радиус (расстояние от оси скважины до рассматриваемого элемента).
| Решение первое для плотных (непористых) | горных пород (задача |
| С. Г. Лехницкого). С. Г. Лехницкий принял допущение, что | |
| σz = рг = const. | |
| Граничные условия: при r = rc σr = pc ; при r =∞ | σr = σt = рб . Решением |
уравнения (4.86) являются формулы, описывающие зависимости σr и σt от r:
| σr = рб – (рб – рс)(rc /r)2 ; | (4.87) |
| σt = рб + (рб – рс)(rc /r)2 . | (4.88) |
Графики, иллюстрирующие формулы (4.87) и (4.88), приведены на рисунке 4.50 (а – случай |σz| >|σt | >|σr|; б – случай |σt| >|σz| >|σr|), из которого следует, что наибольшие изменения напряженного состояния наблюдаются на стенке скважины. Со снижением давления в скважине уменьшаются радиальные напряжения в стенке и увеличиваются тангенциальные напряжения. В пределе тангенциальные напряжения могут превысить вертикальные σz вдвое (при pc = 0
и при pб = pг величина σt = 2σz).
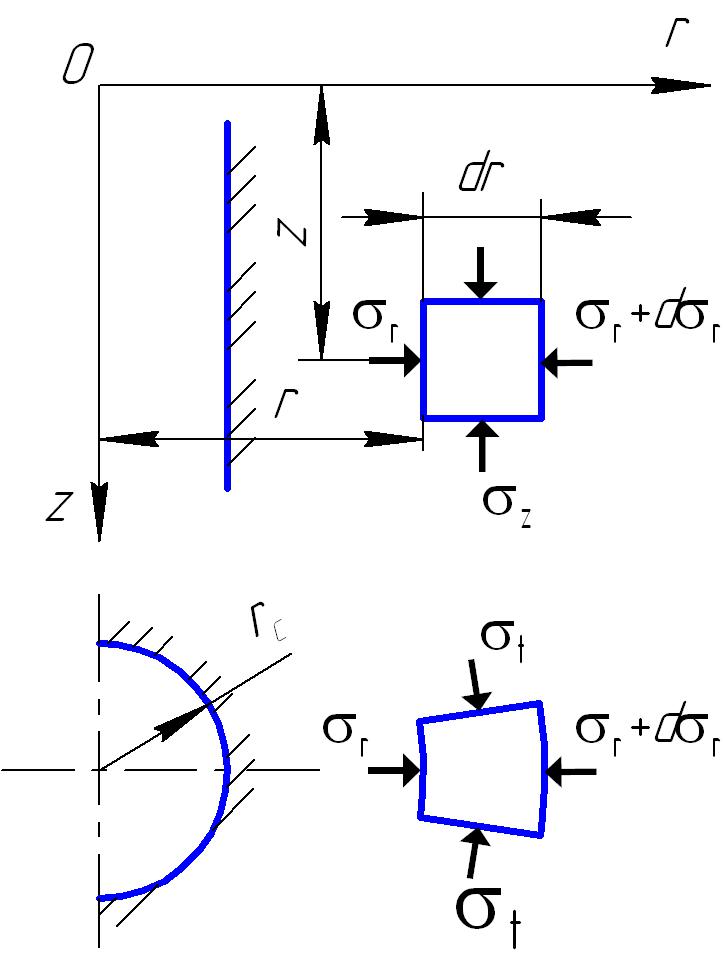
Рис. 4.49. Расчетная схема для определения компонент напряжений вокруг вертикальной скважины
Наибольшее применение при прочностных расчетах стенок скважины находит теория прочности Мора–Кулона, в соответствии с которой предельное состояние горной породы наступает тогда, когда достигает предельного значения максимальное касательное напряжение, причем предельные характеристики горной породы зависят от среднего нормального напряжения в опасном сечении.
Главные нормальные напряжения, а следовательно, и касательные напряжения, принимают максимальные и минимальные значения на стенке скважины. Следовательно, расчетные главные нормальные напряжения следует вычислять при r = rc. Тогда расчетные формулы примут вид
| σz = рг ; | |
| σr = рс ; | (4.89) |
σt = 2рб – рс .
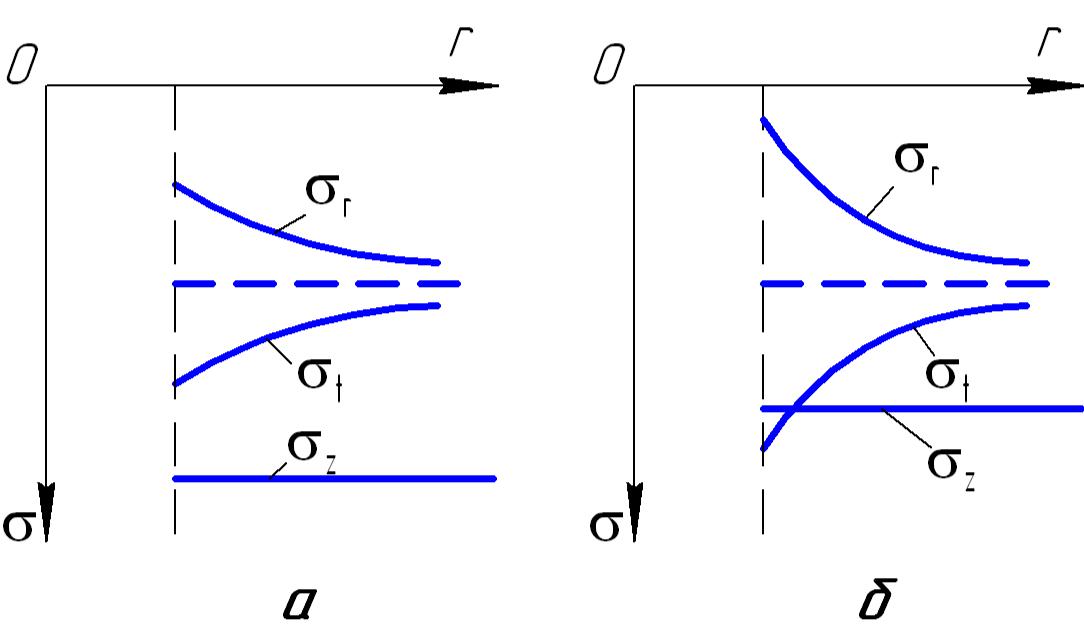
Рис. 4.50. Распределение напряжений вокруг вертикальной скважины
На рис. 4.51 показано возможное разрушение стенок скважины. Штриховкой в клеточку показаны зоны ожидаемого предельного состояния горной пород. На рис. 4.51 а это кольцевые зоны, а на рисунке 4.51 б это продольные вдоль образующей скважины зоны. При разрушении стенки в первом случае следует ожидать образование каверн, а во втором случае – продольное разрушение с образованием желобов.
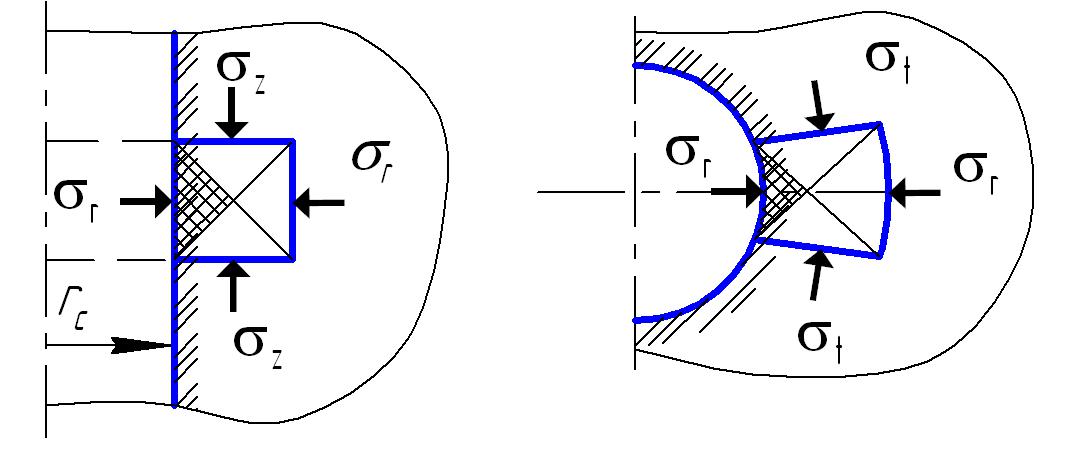
Рис. 4.51. Схема разрушения горной породы на стенке скважины
Решение второе для пористых горных пород.В случае непроницаемойстенки скважины формулы С. Г. Лехницкого при r = rс примут вид
| σz = σ3 ; | |
| σr = рп + (рс – рп)/ с ; | (4.90) |
| σt = 2σ1 – σrc , |
где σ1 и σ3 – естественные горизонтальное и вертикальное напряжения в ске-лете горной породы до вскрытия скважиной, определяются по формулам (4.11) и (4.10).
Решение третье –стенка скважины проницаемая и в ее порах по мереудаления от стенки давление изменяется от давления, равного давлению в скважине, до величины пластового давления. При получении решения сделано допущение, что давление флюидов в порах стенки скважины равно рс. Тогда с учетом необходимых преобразований при r = rc
| σz = σ3 – (рc – pп)(1 – с)/с; | |
| σr = рс; | (4.91) |
| σt = 2σ1 – pc . |
Из формул (4.90) и (4.91) следует, что напряженное состояние в скелете стенки скважины существенно зависит как от давления в скважине, так и от пластового давления и пористости горной породы, характеризуемой долей с скелета.
Дата добавления: 2019-02-22; просмотров: 416; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
