Упругие свойства горных пород. Коэффициент бокового распора
Упругие свойства горных пород характеризуются модулем Юнга (Есж) и коэффициентом Пуассона (μсж), определяемым методом одноосного сжатия модулем деформации (С) по штампу. В задачах механики горных пород основное применение находят μсж и С.
Модуль деформации (упругости) при вдавливании. Анализ результатов определения показателей свойств горных пород, полученных
| Ю. Ф. Алексеевым и Н. М. Филимоновым, показал | зависи- |
| мость модуля деформации от предела текучести | горных пород (р0). |
| На рис. 4.30 эта зависимость представлена графически. Эксперименты вы- | |
полнены при вдавливании штампов диаметром 1,5 и 2,0 мм. На график нанесены данные как по песчано-глинистым (глинистые сланцы, аргиллиты и песчаники), так и по кристаллическим породам ( каменная соль, ангидрит, известняк и доломит). Влияния вида горных пород не наблюдалось, а поэтому точки для разных пород не выделены. Зависимость С от р0 , как следует из рис. 4.30, распадается на две области. В первой области (р0 < 1500 МПа) модуль С увеличивается прямо пропорционально р0:
С = А р0,
где А – коэффициент пропорциональности, равный 21,6 10,7 с вероятностью 0,90.
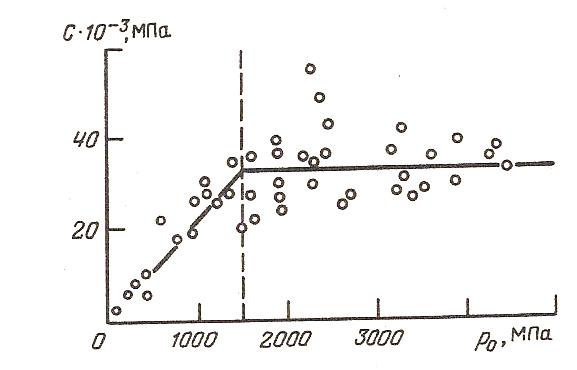
Рис. 4.30. Зависимость модуля упругости С от р 0 осадочных горных пород
Во второй области (р0 > 1500 МПа) величина С стабилизируется в преде-лах С = 32900 14000 МПа. Это обусловлено тем, что модуль упругости горной породы не может быть больше модуля упругости породообразующего минерала. Повышенные значения модуля упругости во второй области наблюдались у доломитов.
|
|
|
Выше отмечалось, что определение показателей свойств горных пород по штампу находится в области существенного проявления масштабного эффекта. Результаты описанного выше изучения влияния масштабного эффекта на проч-ностные характеристики пород были использованы и для модуля упругости. В качестве примера на рис. 4.31 а показана полученная зависимость С от d (d – диаметр штампа) при вдавливании штампов в известняк.
А б
Рис. 4.31. Зависимости С от d (а) и С от x (x = 1/d) (б)
Из рисунка видно, что при малом размере диаметра штампа наблюдалось пониженное значение модуля С и весьма значительный разброс его измеренных значений. По мере увеличения диаметра штампа наблюдается рост модуля С и уменьшение разброса значений. Величина С достигает максимума (в рассматриваемом случае при диаметре штампа 4,5 мм). Затем величина модуля монотонно снижается и стремится к некоторой асимптоте. Одновременно продолжает уменьшаться и разброс его значений.
Диаметр скважины существенно больше возможного диаметра штампа. Поэтому основной интерес для решения задач бурения представляет падающая ветвь зависимости С от d. Результаты испытаний существенно разных горных пород показали , что при вдавливании штампов диаметром 4,5 мм и больше зависимость С от d можно принять гиперболической:
|
|
|
С =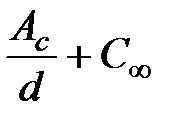 
, (4.69)
где Ас и С∞ – параметры уравнения регрессии; d – диаметр штампа.
Формулу (4.69) удобно представить в линейном виде, т.е. принять в качестве аргумента величину x = 1/d, как показано на рисунке 4.31 б:
С = 
,
Тогда величина С∞ будет равна ординате точки пересечения графика С от х с осью ординат.Полученное уравнение регрессии и высокое значение коэффициента детерминации (R2 = 0,93) подтверждает правильность выбора гиперболической зависимости С от d.
Существующие методы испытаний горных пород по штампу не обеспечивают испытание горной породы при диаметре штампа более 16 мм. Поэтому определение величины асимптоты рекомендуется проводить по результатам испытаний горных пород при трех значениях диаметра штампа 4,5 мм (первый уровень), 8 мм (второй уровень) и 16 мм (третий уровень). На каждом уровне следует выполнить по три-пять испытаний и рассчитать параметры уравнения (4.69) методом регрессии.
|
|
|
Коэффициент Пуассона (модуль поперечной деформации)является вторым важнейшим показателем упругих свойств горных пород. Значения коэффициентов Пуассона горных пород лежат в пределах от 0,10 до 0,45. В таблице 4.11 приведены значения коэффициента Пуассона для некоторых горных пород по данным А. П. Сельващука.
Таблица 4.11
Коэффициенты Пуассона (μ) некоторых горных пород
| Горная порода | μ | Горная порода | μ | |
| Глины пластичные | 0,35–0,45 | Песчаники | 0,25–0,35 | |
| Глины плотные | 0,25–0,35 | Известняки | 0,15–0,35 | |
| Глинистые сланцы | 0,10–0,20 | Ангидриты | 0,30–0,40 | |
| Алевролиты | 0,20–0,30 | Каменная соль | 0,40–0,45 |
Измерения коэффициента Пуассона связаны со значительными техническими трудностями, а поэтому их величины слабо представлены в технической литературе.
Коэффициент бокового распора (λ) представляет собой отношение бокового давления (рб) горной породы к геостатическому (рг) давлению в естественных условиях залегания. Если бы горные породы были идеально упругими телами, то, как следует из закона Гука, величина коэффициента бокового распора горных пород определялась бы однозначно по величине коэффициента Пуассона:
|
|
|
lу = 
, (4.70)
где λу – коэффициент бокового распора идеально упругой горной пород;
μ – коэффициент Пуассона горной породы.
Горные породы не являются идеально упругими твердыми телами, и в них в разной степени проявляется их вязкость, которая обусловливает такие процессы, как релаксация напряжений и ползучесть. Влияние релаксации на λ рассмотрено ниже на примере горной породы с нулевой пористостью.
В естественных условиях имеет место неравномерное напряженное со-стояние горной породы, обусловленное неравенством рг и рб, и в них действуют касательные напряжения, максимальное значение которых
τmax = 0,5(р г – р б) ≠ 0.
Следовательно, в процессе существования горных пород имеют место условия для релаксации напряжений, но при этом изменяться может только боковое давление в сторону его увеличения по абсолютной величине при условии постоянной глубины залегания породы. Геостатическое давление остается постоянным, так как вес вышележащих пород не изменяется (рис. 4.32). В результате процесс релаксации напряжений идет по схеме 1 (кривая 1)
τmax → 0; рб→ рг;λ →1,
если реологическая модель горной породы соответствует модели твердого тела Максвелла, и по схеме 2 (кривая 2)
τmax → τт; рб→ рб∞;λ → λ∞
в случае,когда горная порода соответствует модели твердого тела Шведова, содержащей нерелаксируемое напряжение τт. И только в случаях соответствия горной породы модели Гука (идеально упругое тело) или при |рб| >| рб∞| боковое давление не зависит от времени (кривая 3) рб = рб∞ , а
l = lу = const .
общем же случае имеет место неравенство
| λу ≤ λ∞ ≤ 1 , | (4.71) |
где λ∞ – установившаяся к рассматриваемому моменту времени величина коэффициента бокового распора.
Условие (4.71) существенно затрудняет решение задач, связанных с определением напряжений в горных породах, так как нет надежных методов прямого измерения фактического значения λ.
В случае, когда горные породы залегают в условиях, близких к всестороннему равномерному сжатию, можно принять λ = 1. При этом напряженное состояние характеризуется равенством рг ≈ рб. Это наиболее простой случай для решения задач геомеханики.
| 0 | Время | ||
| 3 | |||
| р бу | |||
| 2 | |||
| Давление | 1 | р б ∞ | |
| р г | |||
Рис. 4.32. Возможные изменения бокового давления горных пород во времени
Абразивность горных пород
Дата добавления: 2019-02-22; просмотров: 2735; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!