17.3. Определение ускорений точек тела
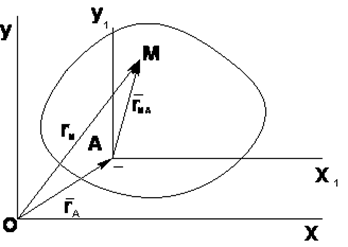
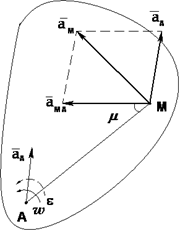
Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.
где 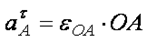 - тангенциальное ускорение полюса, точки А;
- тангенциальное ускорение полюса, точки А; 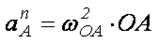 - нормальное ускорение полюса, точки А;
- нормальное ускорение полюса, точки А;
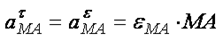 - тангенциальное или вращательное ускорение звена АМ, направлено перпендикулярно к звену АМ;
- тангенциальное или вращательное ускорение звена АМ, направлено перпендикулярно к звену АМ;
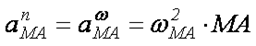 - нормальное или центростремительное ускорение звена АМ, всегда направлено от точки М к полюсу, точке А.
- нормальное или центростремительное ускорение звена АМ, всегда направлено от точки М к полюсу, точке А.
18 Дайте понятие МЦС.
По теореме Эйлера-Шаля любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
В соответствии с этим при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нолю. Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
При определении положения МЦС скорость любой точки может быть записана: VM=VCV+VMCV, где точка СV выбрана за полюс. Поскольку это МЦС и VCV=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей.
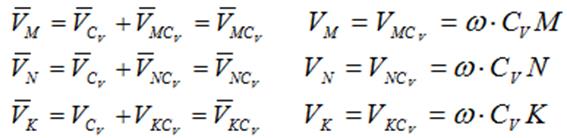
19.Дайте определение абсолютного, переносного и относительного движения точки.
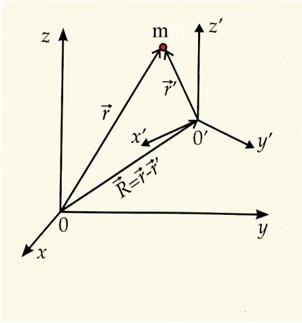
абсолютное движение — это движение материальной точки/тела в базовой системе отсчета(СО). В этой СОрадиус-вектор тела будем обозначать 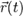 , а скорость тела
, а скорость тела 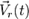 .
.
относительное движение — это движение материальной точки/тела относительно подвижной системы отсчёта. В этой СО радиус-вектор тела 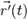 , скорость тела
, скорость тела 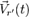 .
.
перено́сное движение — это движение подвижной системы отсчета и всех постоянно связанных с нею точек пространства относительно базовой системы отсчета. Переносное движение материальной точки — это движение той точки подвижной СО, в которой в данный момент времени находится эта материальная точка. Радиус-вектор начала системы координат подвижной СО 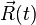 , его скорость
, его скорость 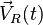 , угловая скоростьвращения подвижной системы отсчета относительно базовой
, угловая скоростьвращения подвижной системы отсчета относительно базовой  . Если эта угловая скорость равна нулю, говорят о поступательном движенииподвижной СО.
. Если эта угловая скорость равна нулю, говорят о поступательном движенииподвижной СО.
Переносная скорость 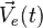 — это скорость в базовой системе отсчёта произвольной точки, зафиксированной относительно подвижной СО, обусловленная движением этой подвижной СО относительно базовой. Например, это скорость той точки подвижной системы отсчёта, в которой в данный момент времени находится материальная точка. В переносная скорость
— это скорость в базовой системе отсчёта произвольной точки, зафиксированной относительно подвижной СО, обусловленная движением этой подвижной СО относительно базовой. Например, это скорость той точки подвижной системы отсчёта, в которой в данный момент времени находится материальная точка. В переносная скорость 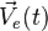 равна
равна 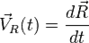 только в тех случаях, когда подвижная СО движется поступательно. Также вводятся и понятия соответствующих ускорений
только в тех случаях, когда подвижная СО движется поступательно. Также вводятся и понятия соответствующих ускорений 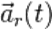 ,
, 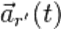 ,
, 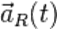 ,
, 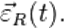 ,
, 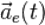 и
и 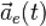 .
.
20. Сформулируйте теорему о сложении скоростей в сложном движении точки.
Если точка М участвует в составном движении, то имеет место следующая теорема: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей этой точки (рис. 116), т. е.
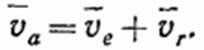

Если угол между векторами 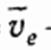 и
и 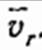 обозначим
обозначим 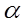 , то модуль и направление вектора абсолютной скорости определяются по формулам:
, то модуль и направление вектора абсолютной скорости определяются по формулам:
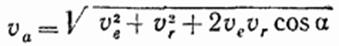
и
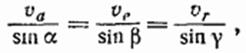
где 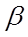 и
и 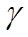 — углы, образуемые вектором
— углы, образуемые вектором 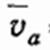 с векторами
с векторами 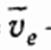 и
и  .
.
21 Теорема сложения ускорений при сложном движении точки
Эта теорема устанавливает связь между абсолютным, относительным и переносным ускорениями точки при сложном движении. Ее называют теоремой Кориолиса по имени доказавшего ее французского ученого.
Теорема Кориолиса
Абсолютное ускорение точки при сложном движении равно геометрической сумме относительного, переносного и кориолисова ускорений.
Доказательство
Запишем полученную при доказательстве теоремы сложения скоростей формулу (33) в виде:
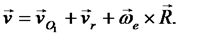
Вычислив полную производную по времени от обеих частей этого равенства, получим
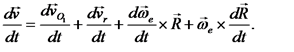 (35)
(35)
В этой формуле полная производная от абсолютной скорости равна абсолютному ускорению
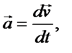
а полные производные от векторов  и
и 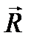 , заданных в подвижной системе координат, следует вычислить по формуле Бура:
, заданных в подвижной системе координат, следует вычислить по формуле Бура:

Тогда выражение (35) перепишется в виде
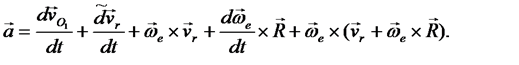
Учитывая, что локальная производная от относительной скорости равна относительному ускорению
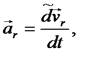
раскрывая скобки и приводя подобные члены из последнего выражения получим
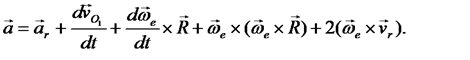 (36)
(36)
Если мысленно остановить относительное движение, положив vr=ar=0, то из формулы (36) получим выражение для переносного ускорения:
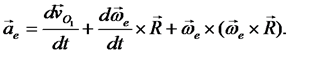
После этого выражение (36) можно переписать в виде
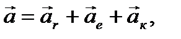 (37)
(37)
где
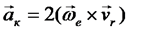 (38)
(38)
ускорение Кориолиса.
Теорема полностью доказана. Она выражается векторным равенством (37).
Поясним далее физический смысл и методы вычисления векторов в правой части равенства (37).
Относительное ускорение характеризует изменение вектора относительной скорости за счет относительного движения. Для его вычисления надо мысленно остановить переносное движение и представить себе, что точка движется по относительной траектории. В зависимости от вида относительной траектории относительное ускорение может иметь одну или две составляющих (см. рис. 24).
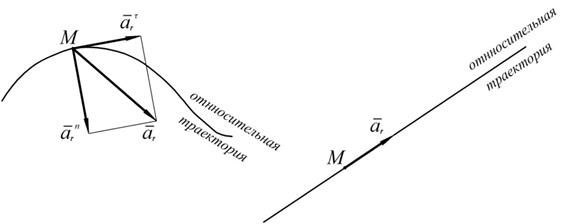
Рис. 24
Переносное ускорение характеризует изменение вектора переносной скорости за счет переносного движения. Для его вычисления надо мысленно остановить относительное движение и представить себе, что точка движется по переносной траектории. В зависимости от вида переносной траектории переносное ускорение тоже может иметь одну или две составляющих (см. рис. 25).
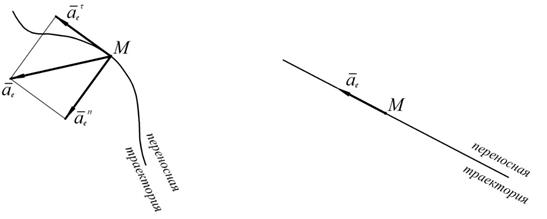
Рис. 25
22. Дайте понятие ускорения Кориолиса.
Ускорение Кориолиса возникает при сложном движении точки только при одновременном выполнении трех независимых условий:
1. Переносное движение должно быть вращательным. То есть угловая скорость переносного движения должна быть не равна нулю.
2. Направление относительного движения не должно быть параллельно оси переносного вращения.
3. Относительное движение должно быть поступательным. То есть линейная скорость относительного движения не должна быть равна нулю.
Для определения направления вектора ускорения Кориолиса необходимо повернуть вектор линейной относительной скорости на 90° в сторону переносного вращения.
Если точка обладает массой, то согласно второму закону Ньютона кориолисово ускорение совместно с массой создадут силу инерции, направленную в сторону противоположную вектору ускорения. Это и есть сила Кориолиса

23.Какие задачи решает кинематика точки и кинематика твердого тела
Кинематика точки изучает движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. Поэтому в кинематике точки скорость, ускорение, координаты всех точек тела считаются равными.
Частные случаи движения в кинематике точки:
· Если ускорение равно нулю, движение прямолинейное (траектория представляет собой прямую) и равномерное (скорость постоянна).
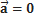
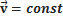
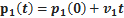
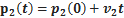
…
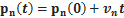
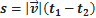
Где s— длина пути траектории за промежуток времени от 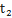 до
до 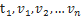 - проекции
- проекции 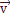 на соответствующие оси координат.
на соответствующие оси координат.
· Если ускорение постоянно и лежит в одной прямой со скоростью, движение прямолинейное, равнопеременное (равноускоренное, если ускорение и скорость направлены в одном направлении; равнозамедленное — если в разные).
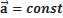
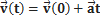
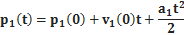

…
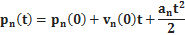
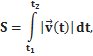
Где s — длина пути траектории за промежуток времени от 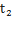 до
до 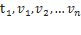 -проекции
-проекции 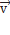 на соответствующие оси координат,
на соответствующие оси координат, 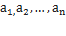 – проекции
– проекции  на соответствующие оси координат.
на соответствующие оси координат.
· Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности — вращательное движение.
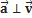
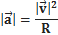
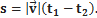
Где R — радиус окружности, по которой движется тело.
Если выбрать систему декартовых координат xyz так, чтобы центр координат был в центре окружности, по которой движется точка, оси y и x лежали в плоскости этой окружности, так чтобы движение осуществлялось против часовой стрелки, то значения координат можно вычислить по формулам:
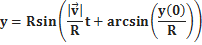
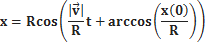
z =0
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
· Если ускорение постоянно и не лежит на одной прямой с начальной скоростью, движение параболическое.
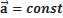
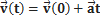
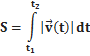
Если выбрать систему декартовых координат xyz так, чтобы ускорение и начальная скорость лежали в плоскости xy и ускорение было сонаправленно с осью y, то значения координат можно вычислить по формулам:
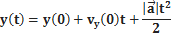
x ( t ) = x (0) + 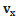 (0) t
(0) t
z =0,
где 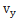 и
и  -проекции
-проекции 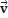 на соответствующие оси.
на соответствующие оси.
Для перехода в другие системы координат используются преобразования Галилея для скоростей намного меньших скорости света, и преобразования Лоренца для скоростей, сравнимых со скоростью света.
· Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.
· В общем виде скорость, ускорение и координаты вычисляются по общим формулам (см. задачи кинематики), путь вычисляется по формуле:
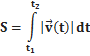
Кинематика твёрдого тела изучает движение абсолютно твёрдых тел (тел, расстояние между двумя любыми точками которого не может изменяться).
Так как любое тело ненулевого объёма имеет бесконечное число точек, и соответственно бесконечное число фиксированных связей между ними, тело имеет 6 степеней свободы и его положение в пространстве определяется шестью координатами (если нет дополнительных условий).
Связь скорости двух точек твердого тела выражается через формулу Эйлера:

Где 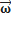 – вектор угловой скорости тела.
– вектор угловой скорости тела.
Основные задачи кинематики твердого тела:
1. задание движения и определение кинематических характеристик движения тела;
2. определение кинематических характеристик движения (траектории,скорости и ускорения) отдельных точек тела.
24. Сформулируйте векторный, координатный и естественный способы задания
Движения точки.
Дата добавления: 2019-02-22; просмотров: 515; | Поделиться с друзьями:
|

Мы поможем в написании ваших работ!
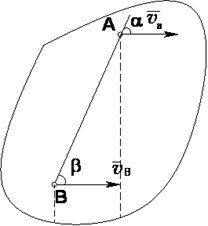
 то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны
то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны  . При этом из теоремы о проекциях скоростей следует, что,
. При этом из теоремы о проекциях скоростей следует, что, 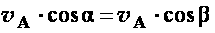 , то есть
, то есть 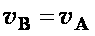 .
.
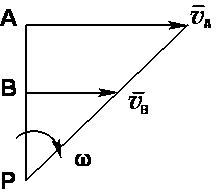
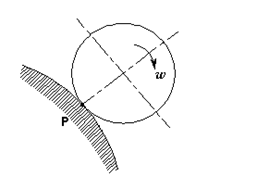
 , то мгновенный центр скоростей определяется построениями, показанными на рисунке. В этом случае кроме направлений скоростей
, то мгновенный центр скоростей определяется построениями, показанными на рисунке. В этом случае кроме направлений скоростей  и
и  , необходимо знать и их модули, чтобы найти P.
, необходимо знать и их модули, чтобы найти P.
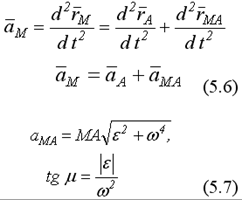
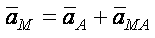

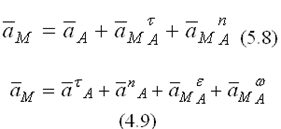
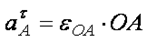 - тангенциальное ускорение полюса, точки А;
- тангенциальное ускорение полюса, точки А; 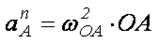 - нормальное ускорение полюса, точки А;
- нормальное ускорение полюса, точки А;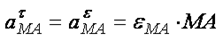 - тангенциальное или вращательное ускорение звена АМ, направлено перпендикулярно к звену АМ;
- тангенциальное или вращательное ускорение звена АМ, направлено перпендикулярно к звену АМ;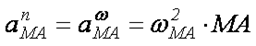 - нормальное или центростремительное ускорение звена АМ, всегда направлено от точки М к полюсу, точке А.
- нормальное или центростремительное ускорение звена АМ, всегда направлено от точки М к полюсу, точке А.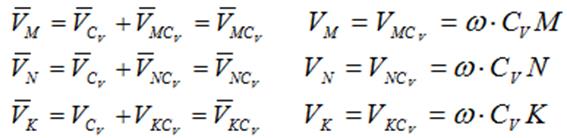

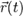 , а скорость тела
, а скорость тела 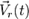 .
.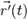 , скорость тела
, скорость тела 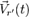 .
.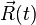 , его скорость
, его скорость 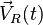 , угловая скоростьвращения подвижной системы отсчета относительно базовой
, угловая скоростьвращения подвижной системы отсчета относительно базовой  . Если эта угловая скорость равна нулю, говорят о поступательном движенииподвижной СО.
. Если эта угловая скорость равна нулю, говорят о поступательном движенииподвижной СО.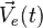 — это скорость в базовой системе отсчёта произвольной точки, зафиксированной относительно подвижной СО, обусловленная движением этой подвижной СО относительно базовой. Например, это скорость той точки подвижной системы отсчёта, в которой в данный момент времени находится материальная точка. В переносная скорость
— это скорость в базовой системе отсчёта произвольной точки, зафиксированной относительно подвижной СО, обусловленная движением этой подвижной СО относительно базовой. Например, это скорость той точки подвижной системы отсчёта, в которой в данный момент времени находится материальная точка. В переносная скорость 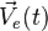 равна
равна 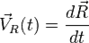 только в тех случаях, когда подвижная СО движется поступательно. Также вводятся и понятия соответствующих ускорений
только в тех случаях, когда подвижная СО движется поступательно. Также вводятся и понятия соответствующих ускорений 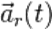 ,
, 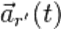 ,
, 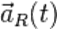 ,
, 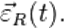 ,
, 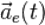 и
и 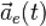 .
.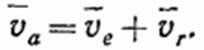

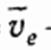 и
и 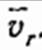 обозначим
обозначим 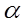 , то модуль и направление вектора абсолютной скорости определяются по формулам:
, то модуль и направление вектора абсолютной скорости определяются по формулам: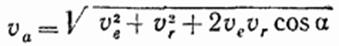
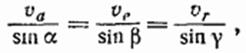
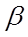 и
и 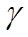 — углы, образуемые вектором
— углы, образуемые вектором 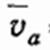 с векторами
с векторами 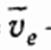 и
и  .
.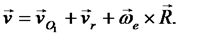
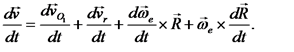 (35)
(35)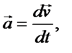
 и
и 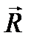 , заданных в подвижной системе координат, следует вычислить по формуле Бура:
, заданных в подвижной системе координат, следует вычислить по формуле Бура:
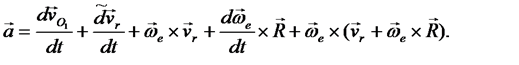
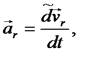
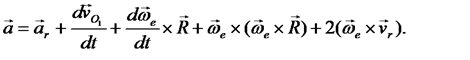 (36)
(36)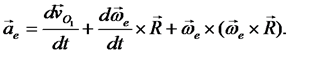
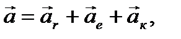 (37)
(37)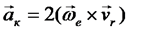 (38)
(38)


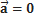
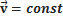
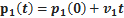
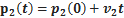
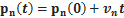
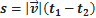
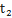 до
до 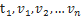 - проекции
- проекции 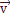 на соответствующие оси координат.
на соответствующие оси координат.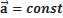
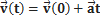
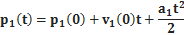

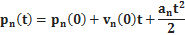
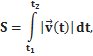
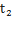 до
до 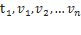 -проекции
-проекции 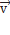 на соответствующие оси координат,
на соответствующие оси координат, 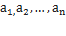 – проекции
– проекции  на соответствующие оси координат.
на соответствующие оси координат.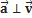
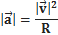
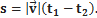
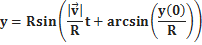
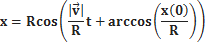
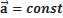
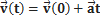
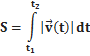
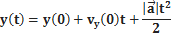
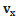 (0) t
(0) t 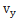 и
и  -проекции
-проекции 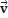 на соответствующие оси.
на соответствующие оси.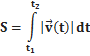

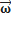 – вектор угловой скорости тела.
– вектор угловой скорости тела.
