Графический расчет плоских ферм.
Расчет фермы методом вырезания узлов может производиться графически. Для этого сначала, определяют опорные реакции. Затем, последовательно отсекая от фермы каждый из ее узлов, находят усилия в стержнях, сходящихся в этих узлах, строя соответствующие замкнутые силовые многоугольники. Все построения проводятся в масштабе, который должен быть заранее выбран. Расчет начинают с узла, в котором сходятся два стержня (иначе не удастся определить неизвестные усилия).
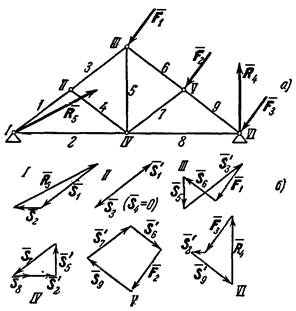
Рис.24
В качестве примера рассмотрим ферму, изображенную на рис. 24, а. В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соотношение выполняется и ферма является жесткой, без лишних стержней. Опорные реакции 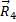 и
и 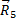 для рассматриваемой фермы, изображаем наряду с силами
для рассматриваемой фермы, изображаем наряду с силами 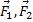 и
и 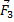 , как известные.
, как известные.
Определение усилий в стержнях начинаем с рассмотрения стержней, сходящихся в узле I (узлы нумеруем римскими цифрами, а стержни - арабскими). Мысленно отрезав от этих стержней остальную часть фермы, отбрасываем ее действие отброшенной части также мысленно заменяем силами 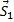 и
и 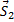 , которые должны быть направлены вдоль стержней 1 и 2. Из сходящихся в узле I сил
, которые должны быть направлены вдоль стержней 1 и 2. Из сходящихся в узле I сил 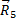 ,
, 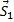 и
и 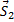 строим замкнутый треугольник (рис. 24, б).
строим замкнутый треугольник (рис. 24, б).
Для этого изображаем сначала в выбранном масштабе известную силу 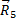 , а затем проводим через ее начало и конец прямые, параллельные стержням 1 и 2. Таким путем будут найдены силы
, а затем проводим через ее начало и конец прямые, параллельные стержням 1 и 2. Таким путем будут найдены силы 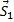 и
и 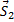 , действующие на стержни 1 и 2. Затем рассматриваем равновесие стержней, сходящихся в узле II. Действие на эти стержни отброшенной части фермы мысленно заменяем силами
, действующие на стержни 1 и 2. Затем рассматриваем равновесие стержней, сходящихся в узле II. Действие на эти стержни отброшенной части фермы мысленно заменяем силами 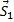 ,
, 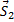 , и
, и 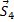 , направленными вдоль соответствующих стержней; при этом сила
, направленными вдоль соответствующих стержней; при этом сила 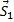 нам известна, так как по равенству действия и противодействия
нам известна, так как по равенству действия и противодействия  .
.
Построив из сил, сходящихся в узле II, замкнутый треугольник (начиная с силы 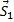 ), найдем величины S3 и S4 (в данном случае S4 = 0). Аналогично находятся усилия в остальных стержнях. Соответствующие силовые многоугольники для всех узлов показаны на рис. 24, б. Последний многоугольник (для узла VI) строится для проверки, так как все входящие в него силы уже найдены.
), найдем величины S3 и S4 (в данном случае S4 = 0). Аналогично находятся усилия в остальных стержнях. Соответствующие силовые многоугольники для всех узлов показаны на рис. 24, б. Последний многоугольник (для узла VI) строится для проверки, так как все входящие в него силы уже найдены.
Из построенных многоугольников, зная масштаб, находим величины всех усилий. Знак усилия в каждом стержне определяется следующим образом. Мысленно вырезав узел по сходящимся в нем стержням (например, узел III), прикладываем к обрезам стержней найденные силы (рис. 25); сила, направленная от узла ( 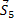 на рис. 25), растягивает стержень, а сила, направленная к узлу (
на рис. 25), растягивает стержень, а сила, направленная к узлу ( 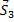 и
и 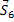 на рис. 25) сжимает его.
на рис. 25) сжимает его.
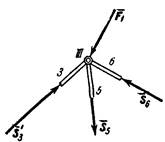
Рис.25
Согласно принятому условию растягивающим усилиям приписываем знак «+», а сжимающим - знак «-». В рассмотренном примере (pиc. 25) стержни 1, 2, 3, 6, 7, 9 сжаты, а стержни 5, 8 растянуты.
13. Метод решения задачи о равновесии системы, состоящей из нескольких тел.
В случае системы твердых тел, соединенных между собой, силы, действующие на эту систему, можно подразделить на две группы:
1) внутренние силы.
2) внешние силы;
Внутренними силами называются силы взаимодействия между телами, входящими в данную систему. По закону равенства действия и противодействия внутренние силы всегда попарно равны по модулю и прямо противоположны по направлению, но приложены к двум разным взаимодействующим между собой телам системы.
Внешними силами называются те силы, с которыми тела, не входящие в данную систему, действуют на тела этой системы.
Рассмотрим, например, систему, изображенную на рис. 39. Балка АВ весом P1, может вращаться вокруг оси А неподвижного цилиндрического шарнира и концом В опирается свободно на другую балку CD весом P2, которая подперта в точке Е и соединена со стеной шарниром D.
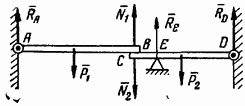
Рис. 39.
В данном случае система состоит из двух тел: балки АВ и балки CD.
Внутренними силами для дгнюй системы являются силы взаимодействия между балками, т. е. сила N2 давления балки АВ на балку CD и сила N1 с которой балка CD действует на балку АВ. По закону равенства действия и противодействия силы N1 и N2 равны по модулю и противоположны по направлению, т. е. N1=-N2.
Веса P1 и P2 балок представляют собой силы, с которыми эти балки притягиваются к Земле, и, следовательно, для данной системы являются силами внешними, так как Земля по отношению к этой системе есть внешнее тело. Реакции RA и RD шарнирных опор А и D, а также реакция RE опоры Е являются для данной системы тоже внешними силами, так как шарнирные опоры А и D и опора Е не принадлежат к рассматриваемой системе, состоящей только из двух балок.
При решении задач на равновесие системы тел необходимо учесть, что все внешние и внутренние силы, приложенные к каждому телу в отдельности, уравновешиваются. Следовательно, в случае плоской системы сил можно составить по три уравнения равновесия для каждого из этих тел в отдельности.
Таким образом, для системы, состоящей из n тел, можно составить всего 3 n уравнений равновесия. Поэтому, если число неизвестных сил в данной задаче не более 3 n, то такая задача является статически определенной. Если же число неизвестных в задаче окажется больше 3 n, то такая задача не может быть разрешена только на основании уравнений статики абсолютно твердого тела и потому является статически неопределенной.
Так как внутренние силы попарно равны по величине и направлены по одной прямой в противоположные стороны, то алгебраическая сумма их моментов относительно любой точки равна нулю и сумма их проекций на любую ось также равна нулю. Поэтому, если составим уравнение равновесия (уравнение моментов относительно какой-либо точки, или уравнение проекций на какую-либо ось) для каждого тела в отдельности и затем все эти уравнения сложим, то в полученном уравнении члены, содержащие внутренние силы, попарно уничтожаются и, следовательно, в это уравнение будут входить только внешние силы.
Таким образом, если система тел находится в равновесии, то внешние силы, приложенные к этой системе, удовлетворяют тем же трем уравнениям равновесия, что и в случае равновесия одного абсолютно твердого тела. Эти уравнения представляют собой условия равновесия внешних сил, действующих на систему.
Из этих уравнении можно найти все внешние реакции, если число этих внешних реакций не больше трех.
Если же число внешних реакций окажется больше трех или если в задаче, кроме внешних реакций, требуется найти неизвестные внутренние силы, то необходимо применять метод расчленения системы, т. е. нужно рассматривать равновесие каждого тела системы в отдельности и для каждого из этих тел составлять уравнения равновесия, учитывая при этом все силы, приложенные к рассматриваемому телу. Если система состоит, например, из двух твердых тел, то, применяя метод расчленения, получим в общем случае всего шесть уравнений равновесия (по три уравнения для каждого тела). Для составления шести уравнений равновесия можно применять еще и другой прием, а именно: составить сначала три уравнения для всей системы в целом (как для одного абсолютно твердого тела) и затем к этим трем уравнениям присоединить три уравнения равновесия, составленные только для одного из двух тел данной системы. Этот второй прием нередко предпочтительнее, так как в уравнения равновесия, составленные для всей системы в целом, входят только внешние силы и потому эти уравнения обычно оказываются проще.
Задачи, относящиеся к равновесию системы твердых тел, в зависимости от вида соединения этих тел между собой можно разделить на следующие четыре типа:
1. Задачи, где тела, входящие в систему, опираются свободно друг на друга.
2. Задачи, где тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров.
3. Задачи, где тела, входящие в систему, соединены между собой при помощи шарнира.
4. Задачи, относящиеся к определению усилий в стержнях плоской фермы.
14 Какое движение тела называется поступательным?
Поступательным называется такое движение твердого тела, при котором любая прямая, неизменно связанная с этим телом, остается параллельной своему начальному положению.
Теорема. При поступательном движении твердого тела все его точки описывают одинаковые траектории и в каждый данный момент имеют равные по модулю и направлению скорости и ускорения.
Доказательство. Проведем через две точки  и
и 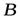 , поступательно движущегося тела отрезок
, поступательно движущегося тела отрезок 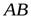 и рассмотрим движение этого отрезка в положении
и рассмотрим движение этого отрезка в положении 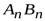 . При этом точка
. При этом точка 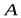 описывает траекторию
описывает траекторию 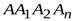 , а точка
, а точка  – траекторию
– траекторию  (рис. 56).
(рис. 56).
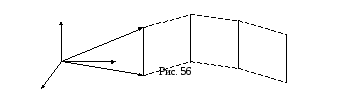 Учитывая, что отрезок
Учитывая, что отрезок  перемещается параллельно самому себе, и длина его не меняется, можно установить, что траектории точек
перемещается параллельно самому себе, и длина его не меняется, можно установить, что траектории точек 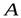 и
и 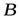 будут одинаковы. Значит, первая часть теоремы доказана. Будем определять положение точек
будут одинаковы. Значит, первая часть теоремы доказана. Будем определять положение точек 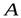 и
и 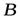 векторным способом относительно неподвижного начала координат
векторным способом относительно неподвижного начала координат 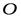 . При этом эти радиусы – вектора находятся в зависимости
. При этом эти радиусы – вектора находятся в зависимости  . Так как. ни длина, ни направление отрезка
. Так как. ни длина, ни направление отрезка 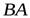 не меняется при движении тела, то вектор
не меняется при движении тела, то вектор 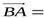
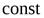 . Переходим к определению скоростей по зависимости (24):
. Переходим к определению скоростей по зависимости (24):
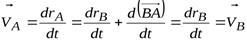 , получаем
, получаем 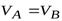 .
.
Переходим к определению ускорений по зависимости (26):
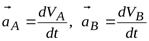 , получаем
, получаем 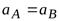 .
.
Из доказанной теоремы следует, что поступательное движение тела будет вполне определено, если известно движение только одной какой- нибудь точки. Поэтому изучение поступательного движения твердого тела сводится к изучению движения одной его точки, т.е. к задаче кинематики точки.
15. Как вычисляются скорость и ускорение точки тела при вращательном движении?
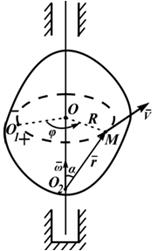
Закон движения точки может быть задан естественным способом (рисунок) траектория – окружность; начало отсчета точка O1 и положительное направление движения выбраны, длина дуги (дуговая координата) определяется по формуле
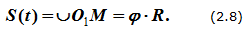
V =ω × r × sin α=ω× R .
Скорость точки определяется выражением
V=dS/dt=dφ∙R/dt=ωR (2.9)
где ω — угловая скорость вращения твердого тела.
Скорость направлена по касательной к траектории, поэтому можно написать
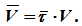
Вектор скорости можно получить векторным произведением:
V =ω × r ,
Ускорение точки при естественном способе задания движения определяется как сумма касательного и нормального ускорений (см. вывод формулы (1.10)):
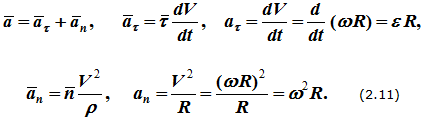
Рисунок 2.5
Эти же выражения можно получить, взяв производную от векторного произведения V=ω × r.
Угол, который составляет полное ускорение с радиусом, может быть определен из соотношения (рисунок 2.5)
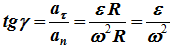
То есть эти углы для всех точек тела одинаковы и не зависят от их расположения на теле. На этом же рисунке представлены законы распределения скоростей и ускорений точек во вращающемся теле в зависимости от расстояния их до оси вращения. Эти законы распределения соответствуют формулам:
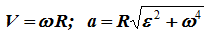
16 и 17 (2в1). Какое движение тела называют плоскопараллельным. Определение скоростей и ускорений точек тела при плоскопараллельном движении.
Плоскопараллельным (или плоским)называется такое движение твердого тела, при котором все его точки перемешаются параллельно некоторой неподвижной плоскости П.
Примерами плоскопараллельного движения могут служить движение колеса на прямолинейном участке пути, движение шатуна кривошипно-ползунного механизма.
Плоскопараллельное движение изучается двумя методами: методом мгновенных центров скоростей и методом разложения плоскопараллельного движения на простейшие движения - поступательное и вращательное.
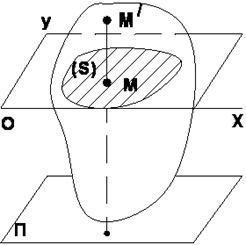
Рассмотрим сечение S тела какой-нибудь плоскостью Oxy, параллельной плоскости П. При плоскопараллельном движении все точки тела, лежащие на прямой ММ/, перпендикулярны к сечению (S), то есть к плоскости Пдвижутся тождественно и в каждый момент времени имеют одинаковые скорости и ускорения. Поэтому для изучения движения всего тела достаточно изучить, как движется сечение S тела в плоскости Oxy.
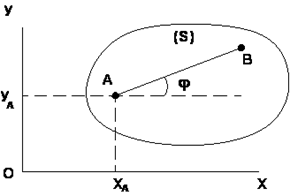
| 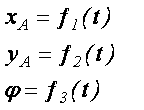 (4.1) (4.1)
|
Уравнения (4.1) определяют закон происходящего движения и называются уравнениями плоскопараллельного движения твердого тела.
Разложение плоскопараллельного движения на поступательноевместе с полюсом и вращательное вокруг полюса
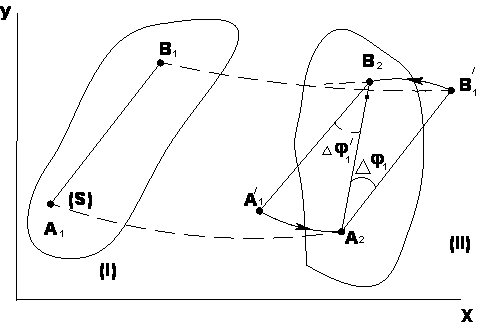
Покажем, что плоское движение слагается из поступательного и вращательного. Для этого рассмотрим два последовательных положения I и II, которые занимает сечение Sдвижущегося тела в моменты времени t1 и t2= t1 + Δt. Легко видеть, что сечение S, а с ним и все тело можно привести из положения I в положение II следующим образом: переместим сначала тело поступательно, так, чтобы полюс А, двигаясь вдоль своей траектории, пришел в положение А2. При этом отрезок A1B1займет положение , а затем повернем сечение вокруг полюса А2 на угол Δφ1. Следовательно, плоскопараллельное движение твердого тела слагается из поступательного движения, при котором все точки тела движутся так же как полюс А и из вращательного движения вокруг этого полюса. При этом следует отметить, что вращательное движение тела происходит вокруг оси, перпендикулярной к плоскости П и проходящей через полюс А. Однако для краткости мы будем в дальнейшем называть это движение просто вращением вокруг полюса А. Поступательная часть плоскопараллельного движения описывается, очевидно, первыми двумя из уравнений (2. 1), а вращение вокруг полюса А - третьим из уравнений (2. 1). Дата добавления: 2019-02-22; просмотров: 405; Мы поможем в написании вашей работы!

Мы поможем в написании ваших работ!
