Условия равновесия произвольной пространственной системы сил.
Контрольные вопросы к разделу «Статика».
1. Дайте понятие силы.
2. Что называется системой сил?
3. Дайте понятие равнодействующей силы.
4. Что называется связью?
5. Сформулируйте аксиомы статики.
6. Дайте понятие пары сил.
7. Дайте понятие момента силы относительно точки.
8. Что называется моментом силы относительно оси?
9. Сформулируйте условия равновесия произвольной плоской системы сил.
10. Сформулируйте условия равновесия произвольной пространственной системы сил.
11. Какие задачи называются статически определенными?
12. Расскажите о методах расчета фермы.
13. Метод решения задачи о равновесии системы, состоящей из нескольких тел.
14. Какое движение тела называется поступательным?
15. Как вычисляются скорость и ускорение точки тела при вращательном движении?
16. Какое движение тела называется плоскопараллельным?
17. Определение скоростей и ускорений точек тела при плоскопараллельном
движении.
18. Дайте понятие МЦС.
19. Дайте определение абсолютного, переносного и относительного движения точки.
20. Сформулируйте теорему о сложении скоростей в сложном движении точки.
21. Сформулируйте теорему о сложении ускорений в сложном движении точки.
22. Дайте понятие ускорения Кориолиса.
23. Какие задачи решает кинематика точки и кинематика твердого тела.
24. Сформулируйте векторный, координатный и естественный способы задания
движения точки.
25. Как определяется скорость точки при векторном, координатном и естественном
|
|
|
способах задания движения точки.
26. Как определяется ускорение точки при векторном, координатном и естественном
способах задания движения точки.
1. Дайте понятие силы.
Сила- мера механического взаимодействия материальных тел, в результате которого взаимодействующие тела могут сообщать друг другу ускорения или деформироваться (изменять свою форму). Так как сила-это векторная величина, то её принято обозначать так. Сила характеризуется точкой приложения, величиной и направлением. За единицу измерения силы принимается (Н).
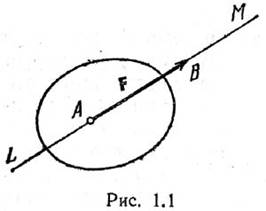
На рисунке показано, как сила приложена к точке A. Отрезок AB= модулю силы F. Прямая LM называется линией действия силы. В сист. СИ сила изм. в ньютонах (Н). Так же есть 1МН=106Н, 1 кН=103Н. Существует 2 способа задания силы:
непосредственным описанием и векторный (ч-з проекции на оси координат). F= Fxi + Fyj + Fzk , где Fx, Fy, Fz – проекции силы на оси координат, а i, j, k - единичные орты.
2 Что называется Системой сил?
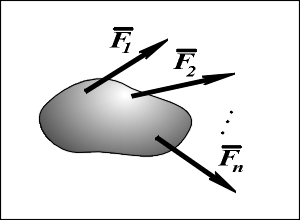 Системой сил называют совокупность сил F1,F2,...,Fn, приложенных к рассматриваемому материальному объекту ( в частности к твердому телу).
Системой сил называют совокупность сил F1,F2,...,Fn, приложенных к рассматриваемому материальному объекту ( в частности к твердому телу).
В зависимости от расположения линий действия сил систему сил называют:
|
|
|
- плоской, если линии действия всех сил лежат в одной плоскости;
- пространственной, если линии действия сил не лежат в одной плоскости;
- системой сходящихся сил, если линии действия всех сил пересекаются в одной точке;
- системой параллельных сил, если линии действия всех сил параллельны друг другу.
Две системы сил называются эквивалентными, если одну систему сил, приложенных к свободному твердому телу, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело.
Система сил называется уравновешенной ( эквивалентной нулю ), если в результате ее приложения к покоящемуся телу она не сообщает телу никакого движения.
Если система сил эквивалентна одной силе, то эта сила называется равнодействующей силой данной системы сил. Сила, равная по модулю равнодействующей силе, противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.
 Закон параллелограмма сил: две силы F1 и F2, приложенные к телу в одной точке, имеют равнодействующую силу R , приложенную в той же точке и являющуюся диагональю параллелограмма, построенного на этих силах, как на сторонах.
Закон параллелограмма сил: две силы F1 и F2, приложенные к телу в одной точке, имеют равнодействующую силу R , приложенную в той же точке и являющуюся диагональю параллелограмма, построенного на этих силах, как на сторонах.
|
|
|
Вектор R называют геометрической суммой векторов F1 и F2 : R =F1+F2.
Модуль равнодействующей может быть вычислен с использованием теоремы косинусов по следующей формуле:
R=(F12+F22+2F1F2cos 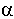 )
) 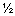 ;
;
где  - угол между силами F1 и F2.
- угол между силами F1 и F2.
Принцип отвердения: равновесие деформируемого твердого тела, находящегося под действием данной системы сил, не нарушится, если тело считать абсолютно твердым.
3. Дайте понятие равнодействующей силы.
Равнодействующая сила F0 - сила, заменяющая собой действие всех остальных сил, приложенных к телу. Вместо множества сил, тянущих тело в разные стороны, удобно использовать одну силу - равнодействующую.
Равнодействующую силу находят сложением векторов всех сил, приложенных к телу. Иногда сложение векторов сил удобно заменить сложением их проекций на координатные оси.
Пример:
 - в этом примере равнодействующая двух сил равна нулю
- в этом примере равнодействующая двух сил равна нулю
(F0y = Fa - Fg = 0)
4. Что называется связью
Механической связью называют ограничения, накладываемые на координаты и скорости механической системы, которые должны выполняться на любом её движении.
Связь можно описать математически как равенство или неравенство, содержащее время, координаты и скорости.
|
|
|
Классификация связей
· Если связь задаётся равенством, то говорят, что такая связь удерживающая или двусторонняя:
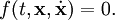
· Если связь задаётся неравенством, то говорят, что такая связь неудерживающая или односторонняя
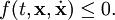
· Если функция 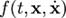 зависит явно от времени, то говорят, что связь нестационарная или реономная. Если эта функция не зависит явно от времени, то говорят что эта связь стационарная или склерономная.
зависит явно от времени, то говорят, что связь нестационарная или реономная. Если эта функция не зависит явно от времени, то говорят что эта связь стационарная или склерономная.
· Если функция не зависит от скоростей, то есть  то говорят, что связь геометрическая илиголономная. Если не существует замена координат, приводящая функцию f к такому виду, то говорят, что связь кинетическая или неголономная.
то говорят, что связь геометрическая илиголономная. Если не существует замена координат, приводящая функцию f к такому виду, то говорят, что связь кинетическая или неголономная.
Сила, с которой связь действует на тело, называется реакцией связи. Если считать силу, с которой тело действует на связь, действием, то сила реакции связи является противодействием. Согласно закону о равенстве действия и противодействия реакция связи равна по модулю силе действия тела на связь, а ее направление противоположно тому направлению, в котором данная связь препятствует перемещению тела. Однако эти силы нельзя считать уравновешенными, хотя они равны по модулю и направлены противоположно, так как точки приложения этих двух сил принадлежат различным телам: действие (давление) приложено к связи, а реакция связи (противодействие) приложена к телу, равновесие которого мы рассматриваем.
Таким образом, все силы, действующие на тело, можно разделить на две группы: силы активные, или задаваемые (сила тяжести, сила упругости сжатой или растянутой пружины и т. п.) и реакции связей. К первой группе следует относить все силы, не являющиеся реакциями связей.
5. Сформулируйте аксиомы статики
Статика – раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил.
Равновесие – такое механическое состояние тела, при котором оно находится в состоянии покоя или движется прямолинейно и равномерно относительно выбранной инерциальной системы отсчёта.
Все тела в природе взаимодействуют между собой и с окружающей средой.
Сила – векторная величина, характеризующаяся величиной (модулем силы), направлением и точкой приложения.
Система тел – совокупность тел, каким-либо образом связанных между собой.
Внутренние силы – силы, с которыми тела данной системы взаимодействуют друг с другом.
Внешние силы – силы, с которыми тела, не входящие в систему, взаимодействуют с телами данной системы.
Равнодействующая сила – это сила, равная эквивалентной системе сил по своему действию.
Система сходящихся сил – это такая система сил, линии действия которой пересекаются в одной точке.
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая движение и/или положение тела или системы тел.
Равновесие механической системы – состояние механической системы, находящейся под действием сил, при котором все её точки покоятся по отношению к рассматриваемой системе отсчёта.
Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называется эквивалентными.
Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой.
Аксиомы статики:
· не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил
· о действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению
· о двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны
· о равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах
· аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания
· аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.
6. Дайте понятие пары сил.
Система двух равных по величине, антипараллельных и не лежащих на одной прямой сил (F1 F2), называется парой сил.
Плоскость, в которой расположена пара сил, называется плоскостью действия пары. Кратчайшее расстояние d между линиями действия сил пары называется плечом пары. Совокупность нескольких пар, действующих на тело, называется системой пар.
Пара сил не имеет равнодействующей, т.е. не может быть заменена одной эквивалентной ей силой.
Теорема. Сумма моментов сил пары относительно любого центра равна моменту пары.
Понятие момента пары можно было бы определить как сумму моментов сил пары относительно некоторой точки. Из теоремы следует, что эта сумма не зависит от выбора точки и совпадает с определением момента пары.
7. Дайте понятие момента силы относительно точки
Представим себе твердое тело, которое может вращаться вокруг неподвижной оси, перпендикулярной к плоскости рисунка и пересекающей эту плоскость в точке О (рис.1.23). Пусть на это тело действует силы, лежащие в этой же плоскости, например, F1 и F2. Такое тело называется рычагом. Эффективность силы, приложенной к рычагу и стремящейся повернуть его вокруг оси вращения, определяется величиной и направлением момента этой силы относительно точки О.
В общем случае центром моментов может быть любая точка, даже не принадлежащая телу. При изучении плоской системы сил момент силы относительно точки рассматривается как алгебраическая величина.
Алгебраическим моментом силы F относительно точки О называется взятое со знаком плюс или минус произведение модуля силы на длину перпендикуляра, опущенного из этой точки на линию действия силы.
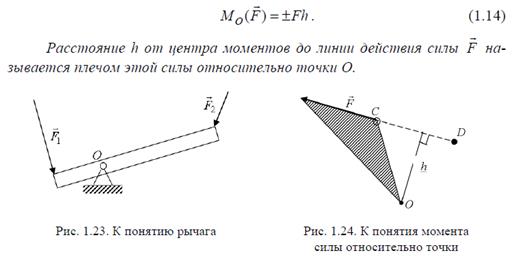
Момент силы относительно точки считается положительным, если сила стремится повернуть тело вокруг центра моментов против хода часовой стрелки, в противном случае – отрицательным.
Момент силы измеряется в Н*м
Свойства алгебраического момента силы относительно точки:
1)при переносе силы по линии действия ее момент не изменяется, так как при этом сохраняются и величина силы, и ее плечо относительно центра моментов
2) момент силы относительно точки равняется нулю, если центр моментов лежит на линии действия силы, так как в этом случае плечо силы равно нулю(рис 1.24) Мd(F)=0
Теорема Вариньона. Алгебраический момент равнодействующей плоской системы сходящихся сил относительно любого центра равен сумме алгебраических моментов сил, составляющих систему, относительно того же центра.
8. Что называется моментом силы относительно оси?

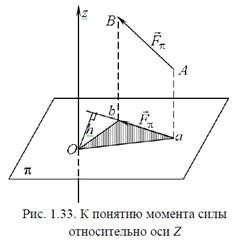

Моментом силы 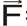 относительно оси z называется момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки О их пересечения
относительно оси z называется момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки О их пересечения
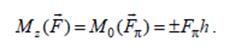
Из этого определения следует, что момент силы относительно оси –алгебраическая величина. Правило знаков: если с конца оси моментов видно, что сила стремится поворачивать тело вокруг этой оси против хода часовой стрелки, то ее момент относительно этой оси будем считать положительным, а если по ходу часовой стрелки – отрицательным.
Момент силы относительно оси обращается в нуль в следующих двух случаях:
1) если сила параллельна оси моментов (в этом случае проекция силы на плоскость, перпендикулярную к оси, равна нулю);
2) если линия действия силы пересекает эту ось (плечо силы Fπ относительно точки О равно нулю).
Эти случаи можно объединить: момент силы относительно оси равен
нулю, если сила и ось моментов лежат в одной плоскости.
9 Сформулируйте условия равновесия произвольной плоской системы сил.
I. 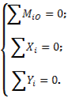
Для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы проекций этих сил на каждую их двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равная нулю.
II. 
Для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно любых трёх точек, не лежащих на одной прямой, были равны нулю.
III. 
Для равновесия плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно любых двух точек А и Ви сумма проекций всех сил на ось Ох, не перпендикулярную прямой, проходящей через точки А и В, были равны нулю.
10. Сформулируйте условия равновесия произвольной пространственной системы сил.
Условия равновесия произвольной пространственной системы сил.
Произвольную пространственную систему сил, как и плоскую, можно привести к какому-нибудь центру О и заменить одной результирующей силой 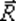 и парой с моментом
и парой с моментом 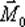 . Рассуждая так, что для равновесия этой системы сил необходимо и достаточно, чтобы одновременно былоR = 0 и Mо = 0. Но векторы
. Рассуждая так, что для равновесия этой системы сил необходимо и достаточно, чтобы одновременно былоR = 0 и Mо = 0. Но векторы 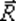 и
и 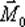 могут обратиться в нуль только тогда, когда равны нулю все их проекции на оси координат, т. е. когдаRx = Ry = Rz = 0 и Mx = My = Mz = 0 или, когда действующие силы удовлетворяют условиям
могут обратиться в нуль только тогда, когда равны нулю все их проекции на оси координат, т. е. когдаRx = Ry = Rz = 0 и Mx = My = Mz = 0 или, когда действующие силы удовлетворяют условиям

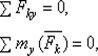

Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.
Условия равновесия произвольной пространственной системы сил.
Произвольную пространственную систему сил, как и плоскую, можно привести к какому-нибудь центру О и заменить одной результирующей силой 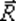 и парой с моментом
и парой с моментом 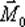 . Рассуждая так, что для равновесия этой системы сил необходимо и достаточно, чтобы одновременно былоR = 0 и Mо = 0. Но векторы
. Рассуждая так, что для равновесия этой системы сил необходимо и достаточно, чтобы одновременно былоR = 0 и Mо = 0. Но векторы 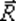 и
и 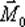 могут обратиться в нуль только тогда, когда равны нулю все их проекции на оси координат, т. е. когдаRx = Ry = Rz = 0 и Mx = My = Mz = 0 или, когда действующие силы удовлетворяют условиям
могут обратиться в нуль только тогда, когда равны нулю все их проекции на оси координат, т. е. когдаRx = Ry = Rz = 0 и Mx = My = Mz = 0 или, когда действующие силы удовлетворяют условиям
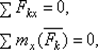
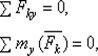

Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.
Дата добавления: 2019-02-22; просмотров: 521; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
