Основное уравнение динамики относительного движения.
До сих пор изучалось движение материальной точки по отношению к инерциальной системе отсчета, т. е. системы отсчета, где справедливы законы Ньютона. Во многих случаях задачи динамики сводятся к исследованию движения в той или иной неинерциальной системе. Рассмотрим движение точки по отношению к подвижной системе отсчета
Основное уравнение динамики относительного движения материальной точки будет иметь вид
, (4.1)
где 
– ускорение точки относительно подвижной системы отсчета
Относительное движение материальной точки происходит под действием приложенных к точке сил, при условии, что к ним присоединены переносная 
и Кориолисова 
силы инерции.
При этом переносная и Кориолисова силы инерции – это векторы, численно равные произведению массы точки на ее 
переносное и 
Кориолисово ускорения. Направление сил инерции противоположно направлению одноименных им ускорений.
Условие относительного покоя можно получить из основного уравнения динамики относительного движения материальной точки путем подстановки в указанное уравнение нулевых значений и :
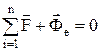, (4.2)
Примеры решения задач
Задача 1
Шарик М массой m = 0.2 кг движется со скоростью V = 19.62 м/с относительно вертикальной трубки, которая на расстоянии l = 0.5 м прикреплена к вертикальному валу 1. Вал вращается с постоянной угловой скоростью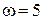 
рад/с. Определить переносную силу инерции шарика.
|
|
|
Решение
Переносная сила инерции может быть рассчитано согласно формулы: 
, Определим переносное ускорение точки.
Так как переносным движением является вращение трубки вокруг оси Z, то переностным движением точки является движение по окружности радиуса 
. При этом ускорение точки можно разложить на два ускорения ( 
и 
), т.е.:
;
м/с2;
; 
м/с2.
м/с2; 
Н.
Ответ: 
.
Задача 2
Штатив с математическим маятником движется по наклонной плоскости вниз с ускорением 
. Определить угол 
в положении относительного покоя шарика, если угол 
.
Решение
Запишем основное уравнение динамики относительного покоя 
.
Спроецируем это уравнение на ось Х и Y, при этом учтем, что 
.
OX: 
(1)
OY: 
(2)
Из уравнения (2) выразим T и подставим в уравнение (1).
; 
, 
; 
, 
;
т.к.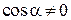 
.
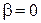Ответ: .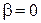
Теорема о движении центра масс механической системы
Механическая система – любая совокупность взаимосвязанных между собой материальных точек. Действующие на механическую систему силы подразделяются на внешние ( 
) и внутренние ( 
), активные ( 
) и реакции связей ( 
).
Внешние силы – силы, действующие на точки (тела) механической системы со стороны точек (тел), не входящих в данную механическую систему. Внутренние силы – это силы взаимодействия между материальными точками (телами) самой механической системы.
|
|
|
В силу третьего закона Ньютона главный вектор и главный момент внутренних сил относительно произвольной точки O равны 0.
; 
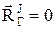, (5.1)
Несмотря на это, движение системы происходит под действием внешних и внутренних сил.
Центром масс или центром инерции механической системы называется геометрическая точка, положение которой определяется радиусом-вектором:
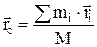, (5.2)
, 
, 
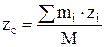, (5.3)
где 
– масса i-й материальной точки системы;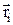 
– радиус-вектор этой точки; 
, 
и 
– координаты точки,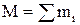 
– масса всей системы.
Теорема о движении центра масс звучит следующим образом: центр масс механической системы движется как материальная точка с массой равной массе всей системы, к которой приложены все внешние силы действующие на систему.
. (5.4)
Из теоремы о движении центра масс механической системы следует, что движение всей механической системы можно рассматривать как движение одной точки – центра масс
|
|
|
Используя вышеописанные уравнения можно определять движение центра масс системы, не определяя движения отдельных ее точек.
Примеры решения задач
Задача 1
Тело 1 массой m1 = 4 кг может двигаться по горизонтальной направляющей. На какое расстояние переместится тело 1, когда однородный стержень 2 массой m2 = 2 кг и длиной l = 0,6 м, опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент система находилась в покое.
Решение
Выберем начало системы отсчета. Расстояние от оси Y до центра масс 1 тела обозначим X1, а до тела 2 X2. Предположим, что при перемещении тела 2 в вертикальное положение вся система сместится вправо на расстояние 
согласно теореме о сохранении положения центра масс. Координата центра масс первого тела будет равна 
, а второго тела 
.
Запишем уравнение для определения центра масс всей системы для 1-го и 2-го положений.
; 
;
Т.к. 
, 
,
; 
;
; 
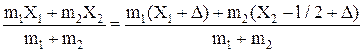м.
Ответ: 
м.
Задача 2
Тело 1 массой m1 = 0,7 кг может двигаться по горизонтальной направляющей. Определить ускорение тела 1 в момент времени t = 0,25 с, если относительно него под действием внутренних сил системы движется тело 2 массой m2 = 0,1 кг согласно уравнению 
.
|
|
|
Решение
Выберем начало системы отсчета. Расстояние от оси Y до центра масс 1 тела обозначим X1, а до тела 2 X2. При перемещении тела 2 в нижнее положение вся система должна сместиться вправо на расстояние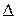 
согласно теоремы о сохранении центра масс. Координата центра масс первого тела будет равна , а второго тела 
.
Запишем уравнение для определения центра масс всей системы в 1-ом и 2-ом положениях.
; 
;
т.к. ,
,
;
;
; 
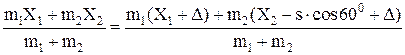м.
Для определения ускорения 1-го тела необходимо дважды продифференцировать полученную зависимость:
; 
м/с2.
Ответ: 
м/с2.
Дата добавления: 2019-02-13; просмотров: 734; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!