Требования по технике безопасности

1. Подготовка лабораторной работы осуществляется лаборантом или преподавателем физики при обязательном соблюдении требований техники безопасности.

2. Во время выполнения лабораторной работы не рекомендуется допускать попадания лазерного пучка в глаза.

3. Запрещается направлять пучок лазера на поверхности, имеющие отражающие покрытия.

Задание

1. Определение ширины щели при наблюдении дифракции Фраунгофера.

3. 9 . Методика выполнения задания:

Задание 1. Определение ширины щели при наблюдении дифракции Фраунгофера.

1. Установить экран на расстоянии L равным 50 – 100 см от щели.

2. Включить лазер и направить луч в центр экрана.

3. Измерить координаты x минимумов первого, второго и третьего порядков дифракционной картины.

4. Выполнить п. 3 ещё 2 раза увеличив величину L на 20 – 30 см.

5. По формуле (3) определить ширину щели, приняв длину волны лазера 680 нм. Результаты измерений занести в таблицу 6.

6. Вычислить абсолютную и относительную погрешность ширины щели, учитывая систематические ошибки инструментов.

 

Таблица 6. Определение ширины щели

№ изм.	L, см	m	, мм	d, мкм	мкм	Dd, мкм	,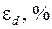
1		1
		2
		3
2		1
		2
		3
3		1
		2
		3

 

Требования к содержанию и оформлению отчета

После выполнения лабораторной работы студент представляет отчёт в следующей форме:

1. Сведения о лабораторной работе:

· номер лабораторной работы;

· название лабораторной работы;

· цель и задачи работы;

· приборы и принадлежности.

2. Методика эксперимента:

· схема установки;

· расчётные формулы.

3. Результаты измерений:

· номер таблицы;

· название таблицы;

· таблица с указанием в графах физических величин, единиц их измерения, погрешностей полученных величин.

4. Оценка погрешностей:

· вывод расчётных формул для вычисления погрешностей;

· вычисление погрешностей измеренных в эксперименте величин;

· вычисление погрешностей косвенных измерений.

5. Выводы:

· краткое изложение полученных результатов;

· сравнение значения ширины щели, полученный экспериментальным путем со значением установки.

· соответствие или несоответствие результатов полученных экспериментальным путем, причины несоответствия.

Критерии результативности лабораторной работы

Лабораторная работа считается выполненной, если студент:

· получил экспериментальные и расчетные данные, соответствующие действительным результатам лабораторной работы;

· выполнил все расчеты согласно требованиям таблиц экспериментальных данных;

· правильно оценил погрешности измерений;

· сформулировал выводы о проделанной работе;

· представил индивидуальный письменный отчет, оформленный в соответствии с предъявляемыми к нему требованиями;

· подготовил ответы на все контрольные вопросы данной лабораторной работы.

Контрольные вопросы

1. Что называется дифракцией света.

2. Сформулируйте принцип Гюйгенса-Френеля.

3. В чем различие дифракции Френеля от дифракции Фраунгофера?

4. Сформулируйте условие дифракционного минимума и максимума для дифракции Фраунгофера.

5. Выведите формулу (3), используя условие дифракционного минимума и рисунок 10.

6. При каком значении ширины щели в дифракции Фраунгофера не наблюдается дифракционного минимума.

7. Запишите условие, при котором дифракцию Фраунгофера можно наблюдать без линзы.

8. Как определить число максимумов, наблюдаемых в дифракции Фраунгофера.

Список литературы

1. Детлаф А. А. Яворский Б.М. Курс физики: учебное пособие. – 8-е изд., стер. – М.: Академия, 2009. – 720 с.

2. Савельев И. В. Курс общей физики. В 5 т. Т. 1. Механика: учебное пособие. – СПб.: Издательство «Лань», 2011. – 352 с.

3. Трофимова Т. И. Курс физики. – М.: Высшая школа, 2012.

4. Трофимова Т. И. Физика в таблицах и формулах: учебное пособие для студентов высших учебных заведений, обучающихся по техническим специальностям. – 3-е изд., испр. – М.: Академия, 2009. – 448 с.

Лабораторная работа № 4

Дифракционная решетка

Цель работы

– Ознакомление студентов с методикой измерения длины световой волны с помощью дифракционной решетки.

4.2. Задача работы:

– Измерить длину световой волны с помощью дифракционной решетки.

Введение

С развитием волновой теории разрабатывались приборы и устройства, принцип работы которых основывается на волновых свойствах света. Основным оптическим прибором для наблюдения явления дифракции света является дифракционная решетка, представляющая собой совокупность большого числа параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Дифракционная решетка позволяет раскладывать белый свет на спектр.

Различают два вида дифракционных решеток: отражательные и прозрачные.

В отражательных дифракционных решетках штрихи нанесены на зеркальную или металлическую поверхность, при этом наблюдение ведется в отражённом свете. Одним из простейших и распространённых примеров отражательной дифракционной решётки является компакт-диск. На поверхности компакт-диска нанесена дорожка в виде спирали с шагом 1,6 мкм между витками. Примерно треть ширины этой дорожки занята углублением – рассеивающим падающий на него свет, примерно две трети – нетронутая подложка, отражающая свет.

В прозрачных дифракционных решетках штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), при этом наблюдение ведется в проходящем свете. Такая дифракционная решетка лежит в основе создания спектроскопа – оптического прибора предназначенного для визуального наблюдения спектра излучения. С помощью данного прибора в промышленности определяют химический состав стали, в астрономии – химический состав звезд и т. д. Также прозрачная дифракционная решетка применяется в спектрометре – оптический прибор, используемый в спектроскопических исследованиях для количественного и качественного анализа содержания химических элементов в веществах. В технике дифракционные решетки применяют в качестве оптических датчиков линейных и угловых перемещений.

4.4. Компетенции, формируемые в результате выполнения
лабораторной работы

В результате выполнения лабораторной работы формируются следующие компетенции:

· способность демонстрировать базовые знания в области общенаучных дисциплин и готовность использовать основные законы в профессиональной деятельности;

· способность проводить эксперименты по заданной методике, обработку результатов, оценку погрешности и достоверности их результатов;

· способность сопоставлять экспериментальные данные с теоретическими положениями;

· способность оформлять, представлять и докладывать результаты выполненной работы.

Перечисленные компетенции формируются через умения:

· работать с измерительными приборами;

· рассчитывать физические величины по экспериментальным данным;

· анализировать результаты опыта;

· оформлять отчет;

а также владения:

· теоретическим материалом;

· навыками измерения физических величин по приборам;

· технологией обработки экспериментальных данных.

Теоретическая часть

При прохождении световой волны через дифракционную решетку дифракционная картина, наблюдаемая на экране, определяется как результат взаимной интерференции волн, идущих от всех щелей. Расстояние между двумя соседними непрозрачными щелями называется периодом d (постоянной) дифракционной решетки. Ширину щели обозначим a.

Рис. 11. Ход лучей через дифракционную решетку: 1 – дифракционная решетка; 2 – линза;3 – экран

На рис. 11 представлена схема хода световых лучей через дифракционную решетку 1, падающие перпендикулярно ее плоскости. В результате дифракции за дифракционной решеткой возникают расходящиеся пучки света. Рассмотрим те параллельные пучки лучей, которые отклонились от первоначального направления распространения на угол j. Пройдя через линзу 2, они собираются на экране 3 и интерферируются в точке P. Очевидно, что в направлениях, в которых ни одна из щелей не распространяет световые лучи, они не будут распространяться и при нескольких щелях. При дифракции на одной щели направление, в котором наблюдается дифракционный минимум, определяется выражением:

.

(1)

Следовательно, при дифракции на множестве щелей минимумы интенсивности по-прежнему наблюдаются в направлениях, определяемых выражением (1) называемая условием главных минимумов.

Параллельные лучи от соседних щелей в направлениях, в которых распространяет световые лучи, имеют некоторую разность хода , зависящую от угла j. Если эта разность хода пропорциональна ml, где m – целое число называемое порядком спектра, то в точке P происходит усиление света. Выражение

(2)

называется условием главных максимумов.

Если разность хода пропорциональна , то в точке P происходит ослабление света. Тогда получим

.

Можно показать, что для дифракционной решетки, состоящей из N щелей, в промежутке между соседними главными максимумами имеется  дополнительных минимума, определяемых выражением

,

(3)

где

Выражение (3) называется условием дополнительных минимумов.

Между соседними дополнительными минимумами располагаются слабые вторичные максимумы. Число таких максимумов, приходящееся на промежуток между соседними главными максимумами, равно . На эти дополнительные максимумы и минимумы накладываются главные минимумы, определяемые условием (1). Вторичные максимумы слабы по сравнению с главными максимумами, и при большом числе щелей они не играют роли. Вторичные максимумы создают слабый фон, на котором выступают узкие и резкие главные максимумы, в которых концентрируется практически весь дифрагированный свет.

Описание установки

На оптической скамье может передвигаться пластина 5, в которой прорезана щель 1 прямолинейной формы (рис. 12). На пластине укреплена шкала с делениями. Щель освещается электрической лампочкой 2. Между лампочкой и щелью вставляется в держатель 6 монохроматический светофильтр. На другом конце оптической скамьи укреплен держатель 3, в который вставляется дифракционная решетка 4. Если смотреть на освещенную монохроматическим светом щель через дифракционную решетку, то по бокам ее видны спектры первого и второго порядков.

Рис. 12. Схема установки: 1 – щель; 2 – лампочка; 3 – держатель для дифракционной решетки; 4 – дифракционная решетка; 5 – пластина со шкалой; 6 – держатель для светофильтра

Пусть спектр первого порядка смещен в сторону относительно центра щели на величину S. Из рис. 12 видно, что

,

где R – расстояние от решетки до щели 1.

Сравнивая последнее выражение с условием главного дифракционного максимума (2) и используя тригонометрические преобразования, получаем расчетную формулу для нахождения длины световой волны:

.

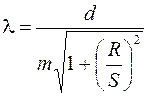(4)

 

---

Дата добавления: 2019-02-12; просмотров: 259; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!