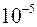Обработка результатов косвенного измерения
К косвенным измерениям прибегают, когда физическую величину нельзя измерить непосредственно или ее непосредственное измерение затруднительно.
В лабораторной практике большинство измерений являются косвенными и интересующая величина f является функцией одной или нескольких непосредственно измеряемых величин 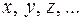 :
:
 . .
| (4) |
Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (4) средних значений непосредственно измеряемых величин, т.е.
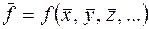 . .
|
Для нахождения абсолютной погрешности косвенных измерений следует пользоваться формулами:
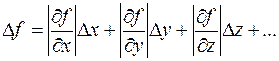 , ,
| (5) |
или
 , ,
| (6) |
где 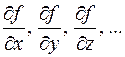 – частные производные функции (4) по аргументу
– частные производные функции (4) по аргументу 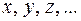 найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные;
найденные в предположении, что все остальные аргументы, кроме того, по которому находится производная, постоянные;  – абсолютные ошибки аргументов.
– абсолютные ошибки аргументов.
Формула (5) вытекает из общего дифференциального метода. Ею удобно пользоваться в случае, если функция имеет вид суммы или разности аргументов. Выражение (6) является частным случаем дифференциального метода, который называется логарифмическим. Её целесообразно применять, если функция имеет вид произведения или частного аргументов.
Пример 2. Определить абсолютную и относительную погрешность длины волны падающего монохроматического света, вычисляемая по формуле
 ,
,
| Таблица 2. Результаты эксперимента | |||||
| k | 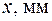
| d, м | 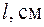
| ||
| 1 | 51 |
| 75 | ||
| 2 | 104 | ||||
| 3 | 155 | ||||
| 4 | 216 | ||||
где d – период (постоянная) дифракционной решетки, x – расстояние от центра дифракционной картины до соответствующих максимумов, l – расстояние от дифракционной решетки до экрана, k – порядок спектра. Измерения величин x и l производились с помощью миллиметровой линейки. Результаты измерений представлены в таблице 2.
Находим 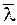 :
:
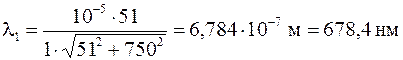 ,
,
 ,
,
 ,
,
 ,
,
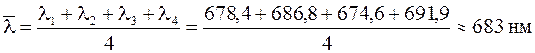 .
.
Находим 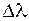 . Воспользуемся формулой (5)
. Воспользуемся формулой (5)
 .
.
Поскольку d и k имеют постоянные числовые значения, то 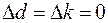 . Тогда
. Тогда
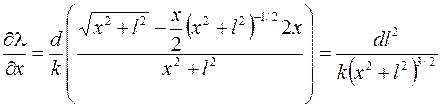 ,
,
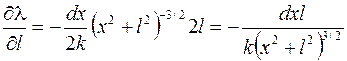 .
.
Окончательно получим
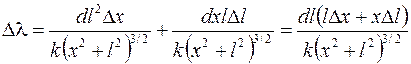 ,
,
где  и
и  – погрешности линейки равные половине цены деления, т.е.
– погрешности линейки равные половине цены деления, т.е. 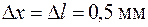 .
.
Абсолютная погрешность длины волны отдельных измерений
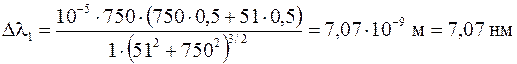 ,
,
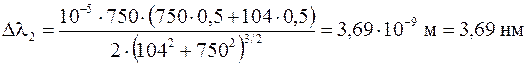 ,
,
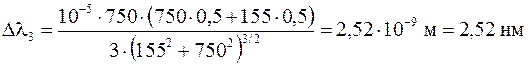 ,
,
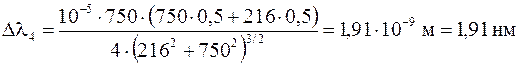 .
.
Абсолютная погрешность по формуле (1) равна
 .
.
Относительная погрешность
 .
.
Окончательно можно записать
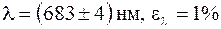 .
.
РАЗДЕЛ 2. Лабораторные работы
по ОПТИКЕ И кВАНТОВОЙ ПРИРОДЕ ИЗЛУЧЕНИЯ
Лабораторная работа № 1
Преломление света
Цель работы
– Изучение закона преломления света в прозрачном однородном твердом веществе.
1.2. Задачи работы:
– Определить показатели преломления различных видов стекла.
Введение
Одним из основных свойств прозрачных твердых тел является абсолютный показатель преломления. От него зависят важные характеристики некоторых оптических приборов, рабочими элементами которых являются прозрачные твердые тела. Например, увеличение микроскопа или телескопа зависит от формы используемых линз, однако основная характеристика линзы – фокусное расстояние зависит от абсолютного показателя преломления стекла, из которого изготовлена сама линза. Компенсатор дисперсии в рефрактометре служит для устранения дисперсии света. Это сложная призма, состоящая из трех простых призм, изготовленных из разного стекла. Подбирая особым образом материал каждой простой призмы, удается устранить дисперсию света.
|
|
|
Прозрачные тела очень часто встречаются в повседневной жизни. Это очки, бинокль, телескоп и т. д. Материал из которого изготовлены рабочие элементы этих оптических приборов, тщательно подбирают. Например, очки, изготовленные из кварцевого стекла, будут обладать большей оптической силой, чем из обычного. Зная абсолютный показатель преломления линзы и ее геометрические размеры можно найти фокусное расстояние.
Существует множество методов нахождения абсолютного показателя преломления прозрачных твердых тел, один из которых рассмотрен в данной лабораторной работе.
1.4. Компетенции, формируемые в результате выполнения
лабораторной работы
|
|
|
В результате выполнения лабораторной работы формируются следующие компетенции:
· способность демонстрировать базовые знания в области общенаучных дисциплин и готовность использовать основные законы в профессиональной деятельности;
· способность проводить эксперименты по заданной методике, обработку результатов, оценку погрешности и достоверности их результатов;
· способность сопоставлять экспериментальные данные с теоретическими положениями;
· способность оформлять, представлять и докладывать результаты выполненной работы.
Перечисленные компетенции формируются через умения:
· работать с измерительными приборами;
· рассчитывать физические величины по экспериментальным данным;
· анализировать результаты опыта;
· оформлять отчет;
а также владения:
· теоретическим материалом;
· навыками измерения физических величин по приборам;
· технологией обработки экспериментальных данных.
Теоретическая часть
В свое время Максвелл пришел к заключению, что свет представляет собой электромагнитную волну. Однако, такие явления, как фотоэффект, давление света, эффект Комптона говорят о том, что свет это поток частиц – фотонов. На самом деле свет – это поток фотонов, обладающие волновыми свойствами.
|
|
|
Электромагнитная волна представляет собой одновременное софазное колебание векторов напряженности электрического 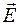 и магнитного
и магнитного 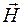 полей во взаимно перпендикулярных плоскостях и перпендикулярно направлению распространения волны.
полей во взаимно перпендикулярных плоскостях и перпендикулярно направлению распространения волны.
Эмпирически установлено, что действие света вызвано в основном колебанием электрического вектора. Магнитное поле с веществами практически не взаимодействует, поэтому под световым вектором обычно принимают вектор 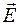 .
.
Световые волны поперечны, но, несмотря на это, ассиметрия относительного луча не наблюдается, т.к. колебания совершаются во всех, перпендикулярных лучу, направлениях. Луч – это линия, вдоль которой переносится световая энергия.
Световые лучи различных длин волн l распространяются в вакууме с одинаковыми скоростями ( 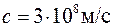 ), а в веществе - с различными. Например, в обыкновенном стекле красный свет распространяется с большей скоростью, чем фиолетовый. Влияние вещества на распространение света обусловлено взаимодействием света со слабо связанными электронами в атоме, из которых состоит вещество. Это взаимодействие ведет к изменению фазовой скорости света u.
), а в веществе - с различными. Например, в обыкновенном стекле красный свет распространяется с большей скоростью, чем фиолетовый. Влияние вещества на распространение света обусловлено взаимодействием света со слабо связанными электронами в атоме, из которых состоит вещество. Это взаимодействие ведет к изменению фазовой скорости света u.
Отношение скорости света в вакууме к фазовой скорости u света в некоторой среде называется абсолютным показателем преломления этой среды
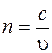 , ,
|
где 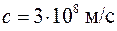 .
.
Однако при переходе из одной среды в другую частота n световой волны не изменяется. Связь длины волны света со скоростью распространения в среде определяется следующей формулой
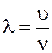 , ,
|
Для световых лучей справедливы следующие законы, называемые законами геометрической оптики.
1. Закон прямолинейного распространения света. В оптически однородной среде свет распространяется прямолинейно.
2. Закон независимого распространения лучей. Световые лучи распространяются независимо друг от друга.
3. Закон отражения света. Угол падения света равен углу отражения, при этом падающий луч, луч отраженный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.
4. Закон преломления света. Падающий луч, луч преломленный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости, при этом
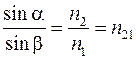 ,
,
где a – угол падения, b – угол преломления, 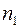 ,
,  – показатели преломления первой и второй сред,
– показатели преломления первой и второй сред, 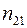 – показатель преломления второй среды относительно первой.
– показатель преломления второй среды относительно первой.
Отношение абсолютного показателя преломления первой среды к абсолютному показателю преломления второй среды называется относительным показателем преломления этих сред
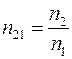 . .
|
Описание установки
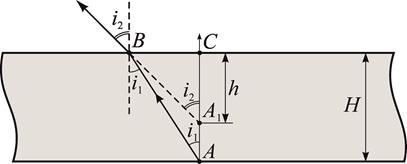
В настоящей работе показатель преломления стекла определяется с помощью микроскопа со встроенным штангенциркулем (рис. 1) и микрометром. В основе применяемого метода лежит явление кажущегося уменьшения толщины стекла при рассматривании сквозь нее метки на нижней грани поверхности стекла. Схема прохождения пучка лучей идущих от источника света до наблюдателя сквозь стеклянную пластинку показана на рис. 2.
Существует связь между действительной толщиной Н исследуемой пластинки, кажущейся толщиной h и показателем преломления стекла n. Установить эту связь можно из рассмотрения хода лучей от точки А через стеклянную пластинку до В. При этом предлагается, что глаз находится на той нормали к плоскости пластинки, которая проходит через точку А, и пучок лучей АВ составляет с нормалью малый угол 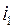 .
.
Узкий пучок лучей АВ после преломления на границе раздела двух сред выходит из пластинки в воздух и составляет с нормалью и ее поверхностью угол  . Согласно закону преломления этот угол связан с углом
. Согласно закону преломления этот угол связан с углом 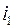 через показатель преломления n следующим соотношением:
через показатель преломления n следующим соотношением:

|
| Рис. 1. Схема установки: 1 – штангенциркуль; 2 – окуляр; 3 – платформа; 4 – ручка окуляра |
 .
.
Наблюдателю кажется, что рассматриваемый пучок лучей исходит не из точки А, а из точки 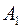 приподнятой на некоторую высоту
приподнятой на некоторую высоту 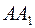 . Рассматривая треугольники АВС и
. Рассматривая треугольники АВС и 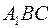 , можно записать, что
, можно записать, что
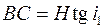 ,
, 
или
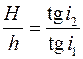 .
.
Принимая во внимание, что углы  и
и 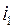 малы, можно отношение тангенсов заменить отношением синусов этих углов, т.е. получить выражение:
малы, можно отношение тангенсов заменить отношением синусов этих углов, т.е. получить выражение:
 .
.
|
| Рис. 2. Распростанение луча в стекляной пластине. |
Таким образом, задача сводится к измерению толщины пластинки H микрометром и кажущейся толщины h микроскопом. Для этого стеклянную пластинку, обозначенную метками с двух сторон, кладут на платформу 3 (рис. 1) микроскопа и, вращая ручку окуляра 4, находят метки верхней и нижней граней. Используя встроенный штангенциркуль 1, определяют координаты высот верхней 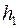 и нижней
и нижней 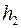 граней. Тогда разность высот и будет являться кажущейся толщиной h стеклянной пластинки. Показатель преломления стекла в этом случае равен
граней. Тогда разность высот и будет являться кажущейся толщиной h стеклянной пластинки. Показатель преломления стекла в этом случае равен
Дата добавления: 2019-02-12; просмотров: 620; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!