РАЗДЕЛ 1. обработка результатов ИЗМЕРЕНИЙ
Классификация измерений
Измерением какой-либо величины называется операция, в результате которой мы узнаем, во сколько раз измеряемая величина больше (или меньше) соответствующей величины, принятой за эталон (единицу измерения). Все измерения можно разбить на два типа: прямые и косвенные.
Прямые – это такие измерения, при которых измеряется непосредственно интересующая нас физическая величина (масса, длина, интервалы времени, температура и т.п.).
Косвенные – это такие измерения, при которых интересующая нас величина определяется (вычисляется) по результатам прямых измерений других величин, связанных с ней определенной функциональной зависимостью (с помощью формул).
Общая черта измерений – невозможность получения истинного значения измеряемой величины, результат измерения всегда содержит какую-то ошибку (погрешность). Объясняется это как принципиально ограниченной точностью измерения, так и природой самих измеряемых объектов. Поэтому, чтобы указать, насколько полученный результат близок к истинному значению, вместе с полученным результатом указывают ошибку измерения.
Обработка результатов прямого измерения
Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины не один раз. Пусть в результате n измерений некоторой величины x получен ряд значений
 .
|
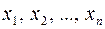Этот ряд значений величины x называется выборкой. Имея выборку можно оценить точность измерения. Наиболее близким к истинному значению измеряемой величины будет ее среднее арифметическое значение 
. Поскольку это значение не представляет собой действительного значения x, необходимо оценить его ошибку (погрешность).
|
|
|
Все ошибки измерения делятся на три класса: промахи, систематические и случайные ошибки.
Промах вызван резким нарушением условий измерения при отдельных наблюдениях. Это ошибка может быть связана с толчком, грубым просчетом экспериментатора, непредвиденным вмешательством и т.д.
Систематической ошибкой называют составляющую погрешности измерений, остающуюся постоянной при повторных измерениях одной и той же измеряемой величины. К систематическим ошибкам относятся в первую очередь инструментальные ошибки, поскольку измерения всегда являются приближенными вследствие ограниченной точности измерительных приборов.
Случайные ошибки проявляются при многократном измерении одной и той же измеряемой величины, дающей различные числовые значения. Причиной случайных ошибок при измерении может быть влияние колебаний температуры в комнате, индивидуальные особенности (реакция) человека и т. д.
|
|
|
Для оценки ошибок измерений обычно рассчитывают абсолютную и относительную погрешности.
Абсолютной погрешностью отдельного i-го измерения Δx i называется модуль разности между средним арифметическим значением измеряемой величины 
и результатом данного измерения x i, т.е.
.
Абсолютной погрешностью измерений 
является среднее арифметическое абсолютных погрешностей каждого измерения
 ,
| (1) |
Отношение абсолютной погрешности измерений Δx к среднему арифметическому значению измеряемых величин называется относительной погрешностью измерений
 .
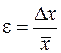| (2) |
Окончательный результат измерений можно записать в виде:
 ,  .
| (3) |
Пример 1. Толщина d плоскопараллельной стеклянной пластины измерялась микрометром. Определить абсолютную и относительную погрешность измерений.
Таблица 1. Результаты эксперимента
| n | 
| 
|
| 1 | 4,02 | 0,024 |
| 2 | 3,98 | 0,016 |
| 3 | 3,97 | 0,026 |
| 4 | 4,01 | 0,014 |
| 5 | 4,00 | 0,004 |
Находим 
.
Абсолютная погрешность измерений по формуле (1) равна
.
Относительная погрешность измерений по формуле (2) равна
.
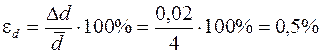Окончательный результат запишем в виде (3)
, 
.
Дата добавления: 2019-02-12; просмотров: 209; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!