Требования по технике безопасности

⇐ ПредыдущаяСтр 6 из 20Следующая ⇒

1. Подготовка лабораторной работы осуществляется лаборантом или преподавателем физики при обязательном соблюдении требований техники безопасности.

2. Включайте источник света не более чем на 30 минут, после чего делайте перерыв на 10 минут.

3. При выполнении лабораторной работы не прикасайтесь к корпусу источника света во избежание ожогов. Перемещайте источник света, касаясь оси или крепления.

4. Запрещается смотреть на источник света через линзу или систему линз.

Задание

Определение продольной хроматической аберрации тонкой линзы.

2.9. Методика выполнения задания:

Определение продольной хроматической аберрации тонкой линзы

1. Установить на оптическую скамью собирающую линзу так, чтобы крестик находился на её главной оптической оси.

2. Включить источник света и переместить его в крайнее левое положение. Переместить экран в крайне правое положение.

3. Установить красный светофильтр в держатель между источником света и линзой. Расположить держатель как можно ближе к крестику.

4. Перемещая линзу добиться увеличенного изображения крестика.

5. Измерить расстояния от крестика до центра линзы a и от центра линзы до экрана b.

6. По формуле (1) вычислить фокусное расстояние тонкой линзы. Результаты измерений записать в таблицу 4.

7. Заменить красный светофильтр оранжевым и повторить пункты 4 – 6.

8. Провести аналогичные процедуры с желтым, зеленым, синим и фиолетовым светофильтрами. Выключите источник света.

9. Построить график зависимости фокусного расстояния тонкой линзы f от длины волны света. Эффективная длина волны пропускания каждого светофильтра можно узнать у преподавателя.

10. Найти продольную хроматическую аберрацию тонкой линзы по формуле (2).

11. Вычислить абсолютную и относительную погрешность фокусного расстояния собирающей линзы для различных длин волн, учитывая систематические ошибки.

Таблица 4. Фокусное расстояние тонкой линзы

№	l, нм	a, cм	b,см	f,см	Df,см	e_f, %
1
2
3
4
5
6
Ds, мм

Требования к содержанию и оформлению отчета

После выполнения лабораторной работы студент представляет отчёт в следующей форме:

1. Сведения о лабораторной работе:

· номер лабораторной работы;

· название лабораторной работы;

· цель и задачи работы;

· приборы и принадлежности.

2. Методика эксперимента:

· схема установки;

· расчётные формулы.

3. Результаты измерений:

· номер таблицы;

· название таблицы;

· таблица с указанием в графах физических величин, единиц их измерения, погрешностей полученных величин.

4. Оценка погрешностей:

· вывод расчётных формул для вычисления погрешностей;

· вычисление погрешностей измеренных в эксперименте величин;

· вычисление погрешностей косвенных измерений.

5. Выводы:

· краткое изложение полученных результатов;

· соответствие или несоответствие результатов полученных экспериментальным путем, причины несоответствия.

Критерии результативности лабораторной работы

Лабораторная работа считается выполненной, если студент:

· получил достоверные экспериментальные данные и выполнил все расчеты;

· оценил систематические погрешности измерений;

· сформулировал выводы о проделанной работе;

· представил индивидуальный письменный отчет, оформленный в соответствии с предъявляемыми к нему требованиями;

· ответил на все контрольные вопросы данной лабораторной работы.

Контрольные вопросы

1. Какую линзу называют тонкой?

2. Что называется главным фокусом линзы? Что называется фокусным расстоянием линзы?

3. Какое изображение в линзе называется мнимым?

4. Какие формулируются правила построения изображения в линзе?

5. Запишите формулу тонкой линзы и поясните каждую ее физическую величину.

6. Как строится изображение предмета в рассеивающей и собирающей линзе?

7. Как меняется величина изображения при удалении предмета от собирающей (рассеивающей) линзы?

8. Как изменится оптическая сила тонкой линзы, если её поместить в воду?

9. Может ли двояковыпуклая линза рассеивать, а двояковогнутая собирать лучи света?

10. Запишите формулу линзы через её радиусы кривизны поверхностей.

11. Что называется оптической силой линзы? В чем её измеряют?

12. Что называется аберрацией?

13. Что называется хроматической аберрацией? Виды хроматической аберрации.

14. Перечислите другие виды аберраций.

Список литературы

1. Детлаф А. А. Яворский Б.М. Курс физики: учебное пособие. – 8-е изд., стер. – М.: Академия, 2009. – 720 с.

2. Савельев И. В. Курс общей физики. В 5 т. Т. 1. Механика: учебное пособие. – СПб.: Издательство «Лань», 2011. – 352 с.

3. Трофимова Т. И. Курс физики. – М.: Высшая школа, 2012.

4. Трофимова Т. И. Физика в таблицах и формулах: учебное пособие для студентов высших учебных заведений, обучающихся по техническим специальностям. – 3-е изд., испр. – М.: Академия, 2009. – 448 с.

Лабораторная работа № 3

Изучение дифракции Фраунгофера
в когерентном свете лазера

Цель работы

– Ознакомиться с установкой для наблюдения дифракции Фраунгофера от щели в когерентном свете лазера.

3.2. Задача работы:

– Определить ширину щели.

Введение

Экспериментально установлено, что свет может огибать препятствия малых размеров и заходить в область геометрической тени. Это явление называется дифракцией света. Используя явление дифракции в промышленности и технике, удалось решить множество научно-технических задач. Например, методом дифракции рентгеновских лучей на кристаллах определяют длину волны рентгеновских лучей с известной структурой кристаллической решётки. Отсюда возникла рентгеновская спектроскопия, сыгравшая важную роль при изучении природы химических связей и количественного анализа веществ. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристалле неизвестной структуры можно установить характер этой структуры (расположение ионов, атомов и молекул, составляющих кристалл). Это послужило основой создания рентгеновского структурного анализа.

Широкий круг задач рентгеновской дифракции и спектроскопии требует высокой чувствительности. Однако рентгеновские лучи практически невозможно фокусировать обычными линзами, поскольку показатель преломления рентгеновских лучей в различных прозрачных для них средах примерно одинаков и очень мало отличается от единицы. Чтобы сфокусировать рентгеновский луч используют волновые свойства излучения и принцип Гюйгенса–Френеля распространения волнового фронта. Для этих целей применяют зонную пластинку – система чередующихся прозрачных и непрозрачных концентрических колец с определенными шириной и диаметром, предназначенная для фокусировки излучения по законам волновой оптики.

3.4. Компетенции, формируемые в результате выполнения
лабораторной работы

В результате выполнения лабораторной работы формируются следующие компетенции:

· способность демонстрировать базовые знания в области общенаучных дисциплин и готовность использовать основные законы в профессиональной деятельности;

· способность проводить эксперименты по заданной методике, обработку результатов, оценку погрешности и достоверности их результатов;

· способность сопоставлять экспериментальные данные с теоретическими положениями;

· способность оформлять, представлять и докладывать результаты выполненной работы.

Перечисленные компетенции формируются через умения:

· работать с измерительными приборами;

· рассчитывать физические величины по экспериментальным данным;

· анализировать результаты опыта;

· оформлять отчет;

а также владения:

· теоретическим материалом;

· навыками измерения физических величин по приборам;

· технологией обработки экспериментальных данных.

Теоретическая часть

Дифракцией света называется огибание световыми волнами препятствий, в результате чего свет отклоняется от прямолинейного распространения.

Основная задача в изучении дифракции света заключается в установлении законов распределения интенсивности света в дифракционной картине (области). Математически эта задача сводится к решению волнового уравнения с соответствующими краевыми условиями. Однако она очень сложна и решена строго лишь для некоторых простейших случаев.

Основные закономерности дифракции света могут быть установлены с помощью принципа Гюйгенса-Френеля, согласно которой «Каждая точка волновой поверхности, до которой дошло возмущение, можно рассматривать как центр вторичного возмущения, порождающая когерентные вторичные сферические волны. Огибающая всей совокупности когерентных вторичных сферических волн определяет новое положение волнового фронта, в каждой точке которой световая волна может быть представлена как результат суперпозиции когерентных вторичных сферических волн».

Различают два вида дифракции света: дифракцию Френеля (рис. 8, а) и дифракцию Фраунгофера (рис. 8, б).

Рис. 8. Дифракция Френеля (слева) и дифракция Фраунгофера (справа)

Дифракцией Френеля (дифракция в сходящихся лучах) называется такая дифракция, при которой дифракционная картина наблюдается на небольшом расстоянии от препятствия.

Дифракцией Фраунгофера (дифракция в параллельных лучах) называется такая дифракция, при которой дифракционная картина наблюдается на большом расстоянии от препятствия.

Если удалить экран (рис. 8, б) и источник света на большое расстояние от щели, то дифракция Френеля переходит в дифракцию Фраунгофера. Таким образом, дифракцию Фраунгофера можно наблюдать и без линзы, если удовлетворяется условие: .

Параллельный пучок от полупроводникового лазера падает нормально на щель шириной d (рис. 8, б). Согласно принципу Гюйгенса-Френеля при прохождении через щель свет дифрагирует. Дифракционные пучки являются когерентными и могут интерферировать при наложении. Результат интерференции в виде периодического распределения интенсивности наблюдается на экране (рис. 9). Распределение интенсивности в получаемой дифракционной картине определяется суммированием элементарных волн, пришедших в данную точку экрана P от всех элементов щели, с учётом их амплитуды и фазы по принципу Гюйгенса-Френеля. Распределение амплитуды света на экране в зависимости от угла дифракции j определяется следующим выражением:

а распределение интенсивности:

(1)

где – интенсивность недифрагированного света на экране, т.е. для случая, когда угол дифракции 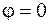. Из формулы (1) видно, что освещённость на экране меняется, принимая минимальные и максимальные значения.

При значениях угла дифракции , удовлетворяющих условию

интенсивность света равна нулю, т.е. 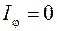, если

(2)

Это есть условие минимума при дифракции Фраунгофера на одной щели – в направлениях, определяемых углом дифракции 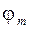щель не «излучает».

Дифракционные максимумы наблюдаются при условии:

Рис. 9. График зависимости интенсивности света от sin j (сверху); вид дифракционной картины на экране (снизу)

График распределения интенсивности на экране показан на рис. 9.

Вид дифракционной картины Фраунгофера зависит от ширины щели. Если, например, ширина щели , то из (2) следует . Следовательно, , т.е. ни одного дифракционного минимума наблюдаться не будет, экран будет весь освещен: больше в середине и меньше по краям. Это соответствует чистой дифракции без интерференции.

Описание установки

Схема установки для наблюдения дифракции Фраунгофера от одной щели, представлена на рис. 10. Лазерный луч, образованный полупроводниковым лазером 1 попадает на щель 2, в результате чего на экране 3 наблюдается дифракционная картина. Пунктирными линиями обозначены направления максимумов. Задача сводится к измерению расстояния 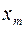от центра дифракционной картины до середины соответствующих минимумов. Зная расстояние от щели до экрана L, длину полупроводникового лазера l, можно вычислить ширину щели по формуле

(3)

Дата добавления: 2019-02-12; просмотров: 253; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!