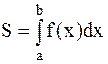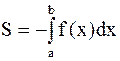Приложения определенного интеграла
Вычисление площади плоской фигуры в
Декартовых координатах
Если задана непрерывная функция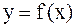 
на [a,b], 
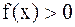, то определенный интеграл с геометрической точки зрения представляет собой площадь так называемой, криволинейной трапеции (рис.4.1).
 | |||
| |||
(4.1)
Пусть криволинейная трапеция с основанием [a,b] ограничена снизу кривой 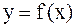(рис.4.2), то из соображений симметрии видим, что
 | |||
| |||
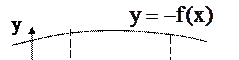(4.2)
В некоторых случаях, чтобы вычислить площадь искомой фигуры, необходимо разбить ее на сумму или разность двух или более криволинейных трапеций и применить формулы (4.1) или (4.2) (рис.4.3. и 4.4)
Пример 43. Вычислить площадь фигуры, ограниченной линиями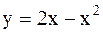 
и 
.
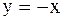Решение.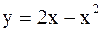 
- парабола. Найдем ее вершину и точки пересечения с осями координат.
; 
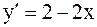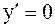или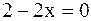 
, 
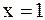
Если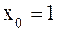 
, то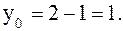 
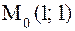- вершина параболы.
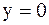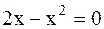или 
или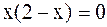 
.
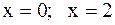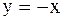- прямая линия.
Найдем абсциссы точек пересечения прямой и параболы:
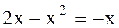или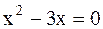 
.
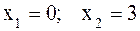Для вычисления площади заштрихованной области воспользуемся формулой (4.4)
|
|
|
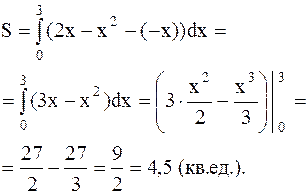
Пример 44. Вычислить площадь двух частей, на которые круг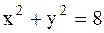 
разделен параболой 
.
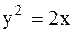Решение. Сделаем чертеж (рис.4.6)
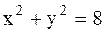- окружность с центром
в начале координат и радиусом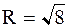 
.
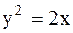- парабола, имеющая вершину
в т.О(0,0)
Найдем точки пересечения параболы
и окружности:
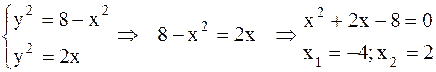
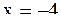- не удовлетворяет условию .
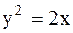Если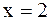 
, то 
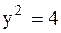или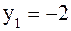 
, 
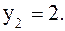
Найдем площадь заштрихованной области по формуле (4.4), в которой изменены переменные интегрирования:
;
.
.
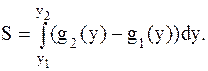
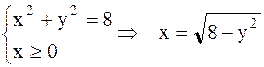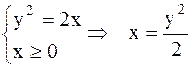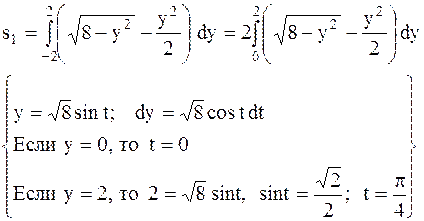
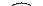
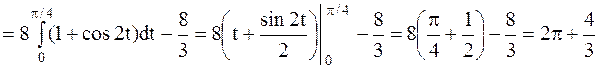Найдем площадь второй (незаштрихованной) части, на которую круг разделен параболой
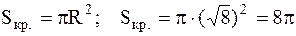
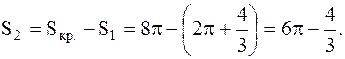
Вычисление площади фигуры, ограниченной линией,
Заданной параметрически
Пусть кривая задана параметрическими уравнениями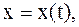 
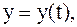то площадь криволинейной трапеции, ограниченной этой кривой, прямым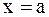и 
и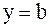 
и отрезком [a,b] оси ОХ, выражается формулой
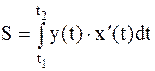, (4.5)
где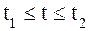 
, 
, 
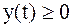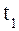и 
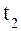определяются из условий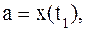 
.
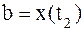Пример 45. Найти площадь фигуры, ограниченной осью ОХ и одной аркой циклоиды
.
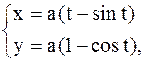
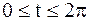Решение. Воспользуемся формулой (4.5). Предварительно найдем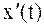 
:
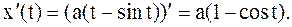
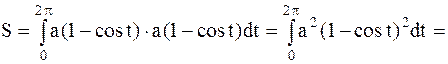
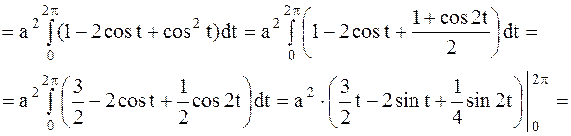
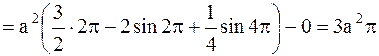(кв.ед.)
Вычисление площади плоской фигуры в
Полярных координатах
В полярных координатах положение точки на плоскости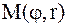 
определяется двумя координатами: полярным радиусом 
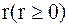и полярным углом j. Связь между декартовыми координатами (x,y) и полярными (j, r) осуществляется по формулам
|
|
|
.
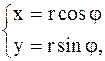
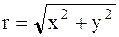Площадь криволинейного сектора,
ограниченного кривой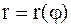 
и двумя
полярными радиусам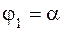и 
и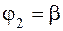 
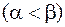(рис.4.7), выражается интегралом
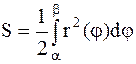. (4.6)
Пример 46. Найти площадь фигуры, ограниченной улиткой Паскаля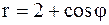 
.
Решение. Воспользуемся формулой (4.6). Чтобы найти пределы интегрирования a и b, необходимо построить чертеж кривой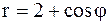 
в полярных координатах. Результаты вычислений занесем в таблицу 1.
Таблица 1
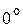
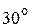
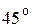
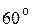
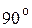
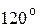
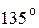
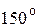
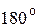
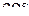| j | 
| 
| 
| 
| 
| 
| 
| 
| 
|
 j
| 1 |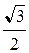 
| 
| 
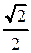
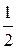
| 0 |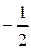 
| 
| 
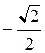
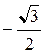
| -1 |
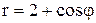
| 3 |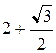 
| 
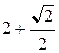
| 2,5 | 2 | 1,5 |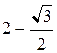 
| 
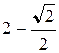
| 1 |
Так как функция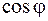 
- четная, то график функции 
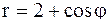строим симметрично относительно горизонтальной оси для значений углов из промежутка 
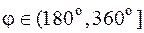. Для построения графика функции при 
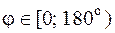проводим полярную ось r; на лучах, составляющих с осью r углы, значение которых указано в таблице 1, откладываем соответствующее расстояние, затем точки последовательно соединяем. Получаем замкнутую кривую, называемую улиткой Паскаля (рис.4.8).
|
|
|
Площадь искомой фигуры равна
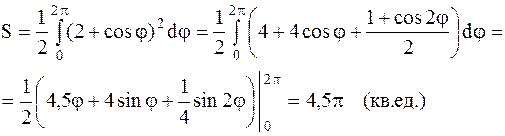
Дата добавления: 2019-02-12; просмотров: 182; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!