Методы вычисления определенного интеграла
Вычисление определенных интегралов как пределов интегральных сумм связано в большими трудностями даже в тех случаях, когда подынтегральные функции являются простыми. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов.
Ниже будет сформулирована теорема Ньютона-Лейбница, позволяющая сводить вычисления определенного интеграла к неопределенному. Эта теорема играет фундаментальную роль в математическом анализе (см.подробнее [1] с.397).
Теорема Ньютона-Лейбница
Пусть f(x) непрерывна на сегменте [a,b] и F(x) - одна из ее первообразных, тогда справедлива формула
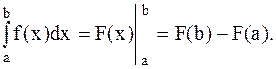
Пример 34. Вычислить 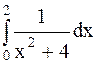 .
.
Решение. Используя формулу Ньютона-Лейбница, а также табличный интеграл 16, получим
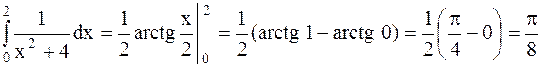 .
.
Методы замены переменной в определенном интеграле
а) Необходимо вычислить интеграл 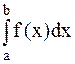 ,
,
где f(x) непрерывная функция на [a,b].
Перейдем к новой переменной t, полагая 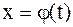 . Пусть
. Пусть 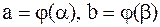 , кроме того, при изменении t от a до b значения функции
, кроме того, при изменении t от a до b значения функции 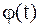 не выходят за пределы сегмента [a,b]. Предположим, что функция
не выходят за пределы сегмента [a,b]. Предположим, что функция 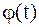 непрерывно дифференцируема на промежутке [a,b], то справедлива следующая формула замены переменной
непрерывно дифференцируема на промежутке [a,b], то справедлива следующая формула замены переменной
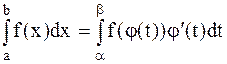 .
.
Пример 35. Вычислить 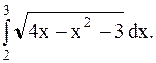
Решение. Преобразуем подкоренное выражение, выделив полный квадрат
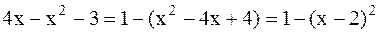 .
.
Введем новую переменную: 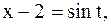 тогда
тогда 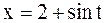 ,
,
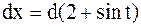 или
или 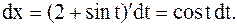
Найдем пределы интегрирования новой переменной t:
если 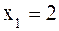 , то
, то 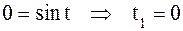
если 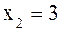 , то
, то 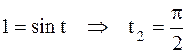 .
.
Воспользуемся формулой замены переменной в определенном интеграле, получим
|
|
|

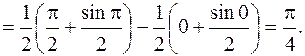
Заметим, что в данном случае при применении формулы замены переменной отпадает необходимость возвращения к старой переменной х по сравнению с неопределенным интегралом. Это вполне объяснимо, ибо определенный интеграл есть некоторое постоянное число, в то время как неопределенный интеграл от той же самой функции есть некоторая функция.
б) Часто вместо замены переменной 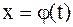 употребляют обратную замену переменной
употребляют обратную замену переменной 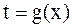 . На конкретном примере покажем, как это делается.
. На конкретном примере покажем, как это делается.
Покажем это на конкретном примере.
Пример 36. Вычислить 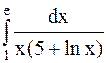 .
.
Решение. Пусть 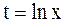 , тогда
, тогда 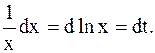
Если 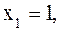 то
то 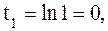 если
если 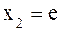 , то
, то 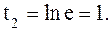
Следовательно,
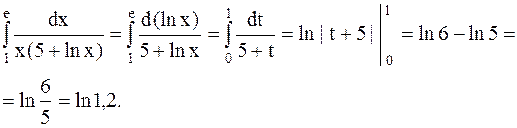
Формула интегрирования по частям в определенном интеграле
Пусть 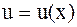 и
и 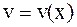 - непрерывные функции вместе со своими первыми производными на [a,b], тогда справедлива формула интегрирования по частям:
- непрерывные функции вместе со своими первыми производными на [a,b], тогда справедлива формула интегрирования по частям:
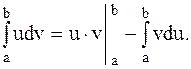
Пример 37. Вычислить интеграл 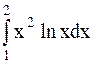 .
.
Решение. Применим полученную формулу
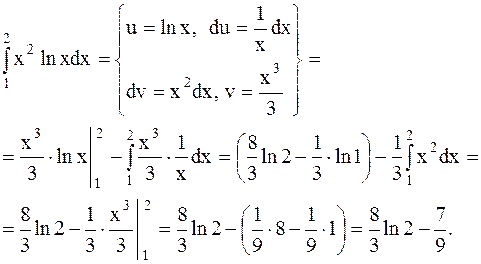
Подробнее о методах интегрирования в определенном интеграле см.[1] с.399-403.
Несобственные интегралы
Определение определенного интеграла, его свойства и методы интегрирования рассматривались в предположении, что промежуток интегрирования [a,b] конечен и функция f(x) непрерывна на нем.
|
|
|
Иногда приходится отказываться от одного или обоих этих предположений. В этом случае мы приходим к понятию несобственного интеграла.
Дата добавления: 2019-02-12; просмотров: 248; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
