Интегрирование некоторых выражений,
Содержащих радикалы
Не от всякой иррациональной функции интеграл выражается через элементарные функции. В дальнейшем будем стремиться отыскивать такие подстановки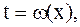 
которые привели бы подынтегральное выражение к рациональному виду. Если при этом функция 
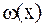выражается через элементарные функции, то интеграл представится в конечном виде и в функции от х.
Назовем этот прием методом рационализации подынтегрального выражения.
1) Интегралы вида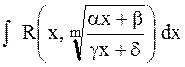 
,
где R означает рациональную функцию от двух аргументов,
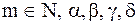- постоянные.
Полагаем,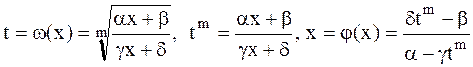 
.
Интеграл приводится к виду
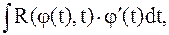
здесь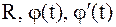 
- рациональные функции.
Вычислив этот интеграл по правилам интегрирования рациональных функций, вернемся к старой переменной, подставив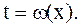 
К интегралу вида (1) сводятся более общие интегралы
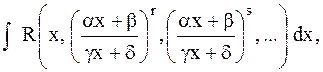
где показатели r, s,… - рациональны.
Нужно привести эти показатели к общему знаменателю m, чтобы под знаком интеграла получить рациональную функцию от х и радикала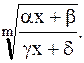 
Пример 22. Найти интеграл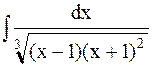 
.
Решение:
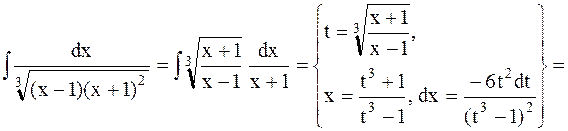
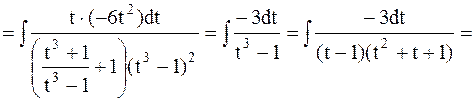
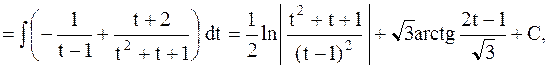
где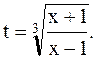 
2) Интегралы вида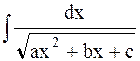 
.
Такие интегралы сводятся к табличному, если в квадратном трехчлене выделить полный квадрат.
Пример 23. Найти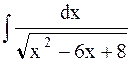 
.
Решение. Преобразуем квадратный трехчлен
.
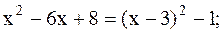
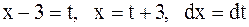Тогда
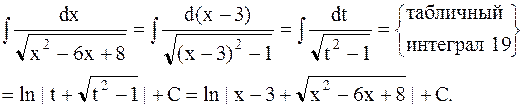
3) Интегралы вида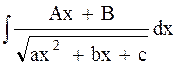 
.
Для отыскания этого интеграла в числителе необходимо выделить такую линейную функцию, которая равнялась бы производной квадратного трехчлена. Далее разбиваем интеграл на сумму двух, один из которых табличный, а второй рассмотрен в предыдущем пункте.
|
|
|
Пример 24. Найти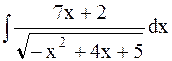 
.
Решение. Выделим в числителе производную подкоренного выражения
.
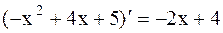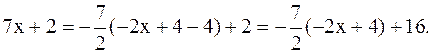
Тогда
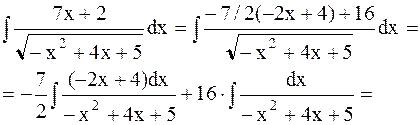
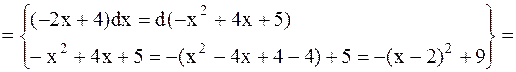
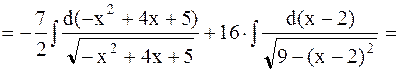
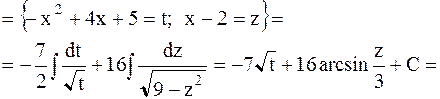
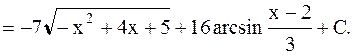
4) Интегралы вида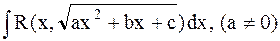 
Эти интегралы приводятся к интегралу от рациональной функции нового переменного с помощью следующих подстановок Эйлера.
I –я подстановка Эйлера. Если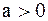 
, то полагаем
.
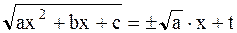Для определенности рассмотрим случай
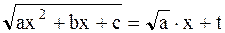. Тогда
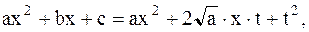
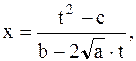то
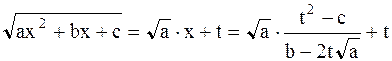- рациональная функция от t, dx также выражается рационально через t.
II -я подстановка Эйлера. Если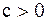 
, то полагаем
.
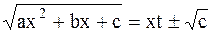Для определенности считаем, что перед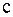 
стоит знак «+». Тогда
.
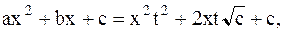
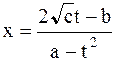При этом dx и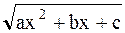 
выражаются рационально через t, поэтому 
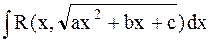сводится к интегралу рациональной функции зависящей от t.
Пример 25. Найти интеграл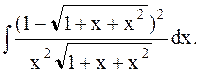 
Решение. Применим 2-ю подстановку Эйлера
;
.
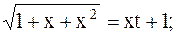
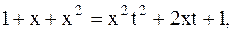
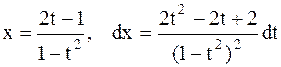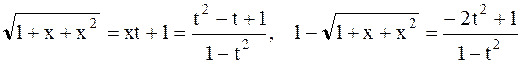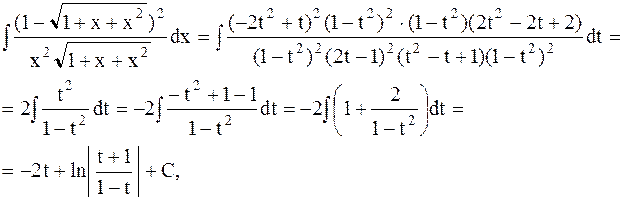
где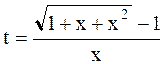 
.
III -я подстановка Эйлера. Квадратный трехчлен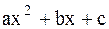 
имеет действительные корни a и b. Тогда 
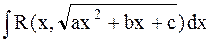сводится к интегралу от рациональной функции от t с помощью замены
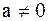
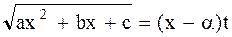или
.
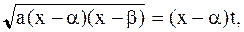
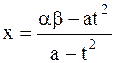Интегрирование биномиальных дифференциалов
Биномиальными называются дифференциалы вида
|
|
|
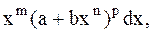
где m,n,p - рациональные числа, a,b - постоянные величины.
Рассмотрим интеграл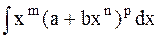 
. (1.5)
1) n - целое число. Данный интеграл сводится к интегралу от рациональной функции от t, если положить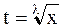 
, l - наименьшее общее кратное знаменателей дробей m и n.
2) 
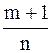- целое число, тогда рационализации подынтегрального выражения можно достигнуть, используя замену
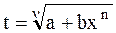, n - знаменатель дроби р.
3) 
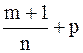- целое.
Замена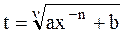 
, n - знаменатель дроби р, позволяет рационализировать подынтегральную функцию в исходном интеграле.
Эти случаи интегрируемости были известны еще Ньютону. Однако, только в середине прошлого столетия П.Л.Чебышев установил факт, что других случаев интегрируемости в конечном виде для биномиальных дифференциалов нет. Поэтому подстановки 1-3 называют подстановками Чебышева.
Пример 26. Найти интеграл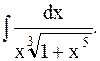 
Решение: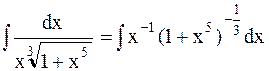 
.
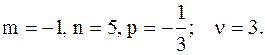
Применим II подстановку Чебышева, т.к.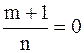 
- целое число
.
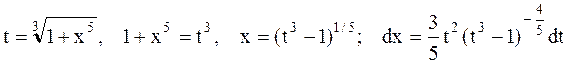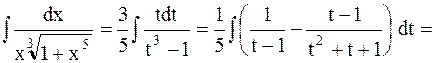
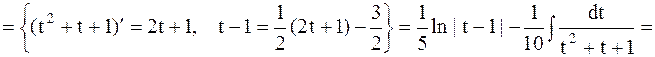
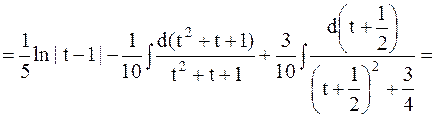
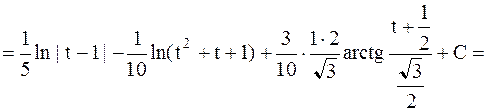
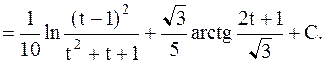
Пример 27. Найти интеграл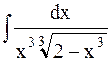 
.
Решение. Подынтегральную функцию можно записать в виде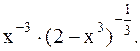 
Здесь 
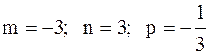и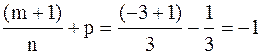 
- целое число. Поэтому имеет место третий случай интегрируемости дифференциального бинома. Произведем замену переменной: 
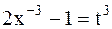, тогда 
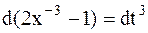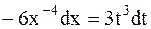или 
или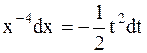 
.
Преобразуем исходный интеграл
|
|
|
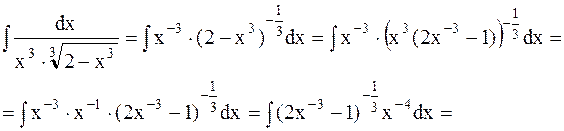
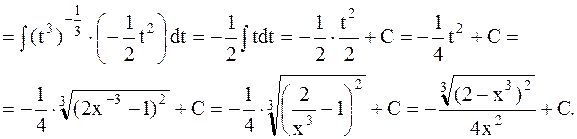
Дата добавления: 2019-02-12; просмотров: 171; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!