Несобственные интегралы с бесконечными
Пределами интегрирования
Рассмотрим функцию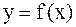 
, непрерывную на бесконечном промежутке 
.
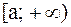Несобственным интегралом от функции f(x) по промежутку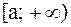 
называется 
:
.
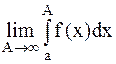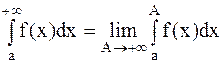Если указанный предел существует и конечен, то несобственный интеграл с бесконечным пределом интегрирования называется сходящимся, в противном случае - расходящимся.
Если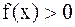 
на 
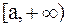и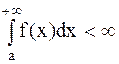 
, то данный интеграл представляет собой площадь бесконечной криволинейной трапеции, ограниченной кривой 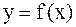, прямой 
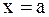и бесконечным интервалом 
.
 |
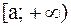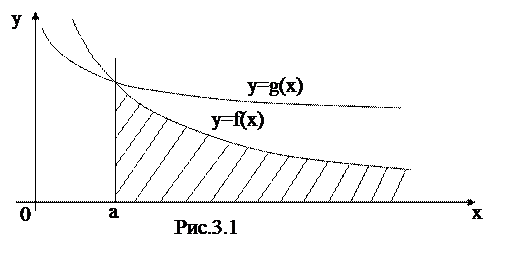Аналогично определяется несобственный интеграл на промежутке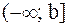 
:
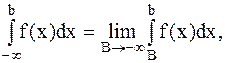
а на интервале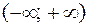 
определяется формулой
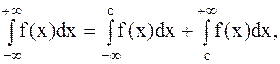
где с - любое действительное число.
Если сравнить две криволинейные трапеции на рис.3.1, то конечность или бесконечность их соответствующих несобственных интегралов зависит от скорости убывания функции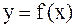 
и 
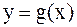при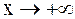 
.
Так, например,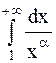 
сходится при 
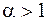и расходится при 
.
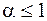В этом легко убедится, вычислив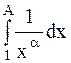 
, если 
.
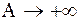Если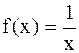 
, то 
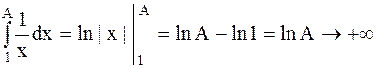при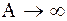 
, поэтому 
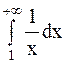- расходится, следовательно, и площадь соответствующей криволинейной трапеции бесконечна.
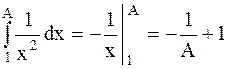
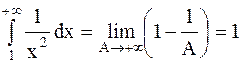- несобственный интеграл сходящийся, следовательно, площадь криволинейной трапеции, ограниченной линиями 
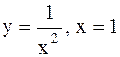и бесконечным промежутком 
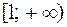, является конечной и равна 1.
Пример 38. Исследовать на сходимость несобственный интеграл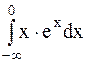 
.
Решение. Воспользуемся определением несобственного интеграла с бесконечным нижним пределом интегрирования и далее - формулой интегрирования по частям
|
|
|
.
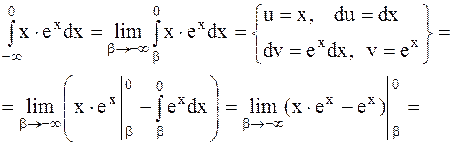
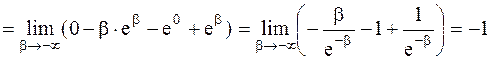Несобственный интеграл сходится.
Пример 39. Вычислить несобственный интеграл или установить его расходимость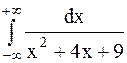 
.
Решение. Воспользуемся определением несобственного интеграла с бесконечными пределами интегрирования. Полагаем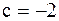 
.
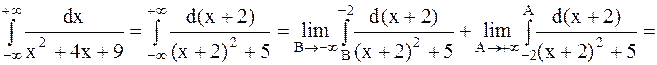
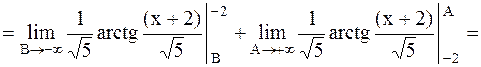
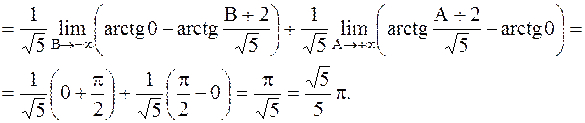
Признак сравнения. Пусть в промежутке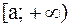 
функции f(x) и g(x) непрерывны и 
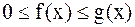. Если 
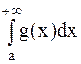сходится, то сходится и интеграл 
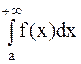. Если интеграл 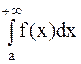расходится, то и 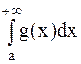также расходится.
Замечание. Аналогичное утверждение верно для несобственных интегралов и по другим бесконечным пределам интегрирования.
Пример 40. Исследовать на сходимость несобственный интеграл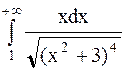 
.
Решение. Проведем сравнительный анализ подынтегральной функции при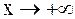 
.
.
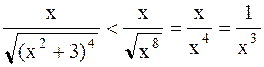
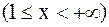Но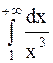 
сходится, т.к. 
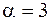(см. рассуждения выше). Следовательно, по признаку сравнения сходится и данный интеграл.
Несобственные интегралы от неограниченной функции
Пусть функция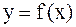 
имеет разрыв II рода на [a,b] либо в точках а и b, либо в точке 
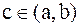, тогда несобственные интегралы от разрывной функции определяются следующим образом:
1) 
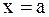- точка разрыва, то
;
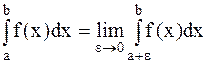2) 
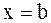- точка разрыва, то
,
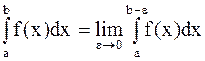3) 
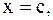
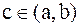, с - точка разрыва, то
|
|
|
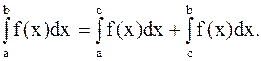
Если указанные пределы существуют и конечны, то несобственные интегралы называются сходящимися, в противном случае расходящимися.
Признак сравнения. Пусть функции f(x) и g(x) в промежутках [a,b) непрерывны, а в точке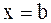 
имеют разрыв II рода; кроме того 
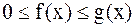. Если 
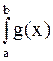сходится, то сходится 
.
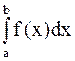Если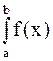 
расходится, то расходится 
.
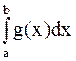Пример 41. Исследовать на сходимость несобственный интеграл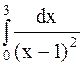 
.
Решение. Функция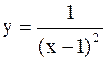 
в точке 
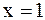имеет разрыв II рода, поэтому
.
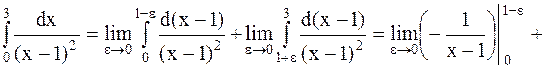
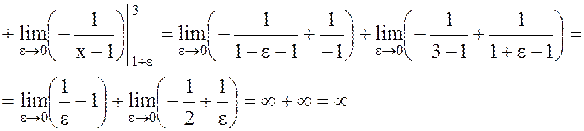Интеграл расходящийся.
Пример 42. Исследовать на сходимость несобственный интеграл от неограниченной функции
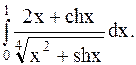
Решение. При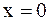 
знаменатель функции обращается в 0, а числитель равен 1, следовательно, 
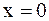- точка разрыва II рода. Во всех остальных точках промежутка (0;1] подынтегральная функция непрерывна.
Заметим также, что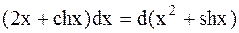 
,
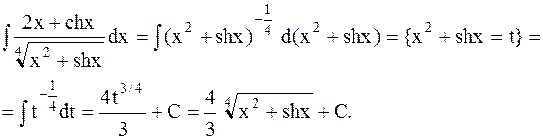
Используя определение несобственного интеграла от неограниченной функции, а также формулу Ньютона-Лейбница получим
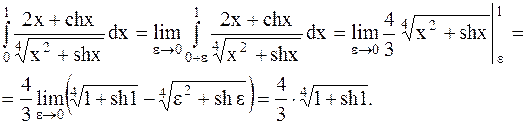
Интеграл сходящийся.
Дата добавления: 2019-02-12; просмотров: 206; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!