Вектор вероятности бифуркационного события с конечным числом исходов

⇐ ПредыдущаяСтр 8 из 12Следующая ⇒

Любое бифуркационное событие при его анализе за счёт факторизации вероятностного пространства или идентификации его исходов может быть на первом этапе рассмотрения сведено к бифуркационному событию с двумя возможными исходами.

Варианты соответствующих исходов могут быть обозначены введением чисел 1–0. 1 – «да» – первый вариант результата события, 0 – «нет» – второй вариант результата события. Для дальнейшего рассмотрения, однако, целесообразнее ввести изоморфный аналог.

1 – первый вариант результата события – «да»,

– 1 – второй вариант результата события – «нет».

Предыдущий опыт («интуицио») позволяет нам с определенной точностью предсказать степень предпочтительности того или иного результата. Пока событие не произошло, мы можем лишь догадываться о том, какой вариант результата будет реализован. Наши догадки, в принципе, могут колебаться между – 1 и +1, при этом колебания обратимы и могут быть охарактеризованы некоторым числом а.

Чтобы понять, какую интерпретацию может иметь число а, можно привести пример.

Пусть имеется желоб длиной 2 см. В какой‑то момент времени на желоб положен шарик. Этот момент можно считать началом события. В точках, расположенных от середины желоба на расстоянии –1 см и +1 см, находятся дырочки, в которые может провалиться шарик. Событие состоит в том, что фокусник катает шарик по желобу, стараясь, чтобы шарик не провалился, и продолжается до тех пор, пока шарик не провалится в одну из дырок. Положение шарика по длине желоба характеризуется тем самым числом а, которое было введено нами выше. Пока шарик не провалился, величина а может принимать любое значение. Все значения а могут быть достижимы. Когда же шарик провалился в одну из лунок – 1 или +1 – событие свершилось. Лунка символизирует один из вариантов результатов события с двумя исходами. Если подобный эксперимент проводить несколько раз, то возникает относительная частота (в пределе при очень больших значениях N, стремящаяся к некоторому числу, называемому нами вероятностью) того, что шарик провалится либо в точку +1 – p₊ = N₊/N, либо в точку –1 – p_‑ = N_‑/N.

Аналогичное рассмотрение может быть проведено в общем (абстрактном) случае. Пусть бифуркационное событие имеет два исхода с вероятностями р₊, p_‑,где обе вероятности могут принимать значения в диапазоне 0–1. В результате события вероятность изменяется таким образом, что либо р₊ = 1, либо р₊ = 0.

Так как р₊+ p_‑ = 1 , то можно ввести параметр α такой, что р₊ = cos²α, p_‑ = sin²α.

Отсюда следует, что величину α можно представить себе в виде единичного вектора α = {α_x, α_y}где α_х = cosα, α_y = sinα. Квадраты проекций вектора α на оси х, у равны соответствующим вероятностям α²_x = р₊, α²_y = Р_‑

Таким образом, выбор того или иного результата события может быть связан с вращением вектора α в двумерном пространстве.

Пусть количество вариантов результатов данного события равно n. В результате события реализуется лишь одна из возможностей. Перед событием существует вероятность реализации каждой из возможностей p_r. Сумма вероятностей реализации каждого из указанных исходов равна единице:

В результате свершения события вероятность реализации одного из результатов окажется равной 1, а вероятность того, что наступит какой‑либо другой исход, окажется равной нулю. Набор вероятностей p – вероятностный вектор – коллапсирует к одному из единичных векторов, то есть он коллапсирует к одному из ортов системы координат, сформированных возможными исходами события.

Итак, перед самым событием существует некоторый вектор р, характеризующий распределение возможностей реализации тех или иных возможных результатов события. Этот вектор может быть назван вектором вероятности будущего события, n‑мерный вектор p перед событием может, в принципе, принимать любые значения на n‑1 – мерном многообразии, имеющем уравнение:

Предыдущий опыт может приближенно подсказать точку на многообразии, соответствующую моменту, предшествующему изучаемому нами событию, однако мы не можем предсказать точно, что произойдет в результате события.

Совсем по иному выглядит картина после происшедшего события. Событие произошло. Определенный результат реализовался, остальные не реализовались. Вектор p принял одно из n возможных значений. Можно сказать, что событие подействовало как оператор, резко уменьшивший область допустимых значений вектора p – c n– 1 – мерного многообразия – до одной из точек.

То же самое можно сформулировать и по‑другому. Соотношения вероятностей попадания системы в одно из возможных состояний до и после события резко изменились. До события система еще имела возможность попасть в любое из допустимых состояний. После события возможность попадания во все состояния, кроме одного, оказались равными нулю.

Наблюдатель системы приобрёл значительную новую информацию не только о настоящем, но и о будущем системы. Здесь, как и ранее для случая с двумя исходами интуитивно появляется понятие информации как результата отождествления системы, которая до свершения события могла с некоторой вероятностью оказаться в одном из возможных состояний с некоторым конкретным состоянием.

Нашему рассмотрению может быть дана и другая математическая интерпретация. Пусть мы имеем фазовое пространство взаимодействующих структур, имеющее n аттракторов – зон притяжения; существует некоторая точка (или область), отделяющая друг от друга бассейны притяжения этих аттракторов. Перед событием фазовое состояние системы взаимодействующих структур попадает в указанную точку или область, выйдя из которой в процессе события оно попадает в бассейн притяжения того или иного аттрактора, откуда ей уже не вернуться назад.

В классической теории вероятностей вместо вектора/) вводится некоторая функция на множестве возможных исходов бифуркационного (случайного) события.

Рассматривается в элементарном случае конечное множество Ω элементов ω, которые мы будем называть элементарными исходами бифуркационного события и ξ(Ω) множество подмножеств из Ω. Элементы множества φ(Ω) будем называть совокупностями исходов бифуркационного события, а Ω – пространством элементарных исходов бифуркационного события.

Каждому элементу ω из Ω поставлено в соответствие неотрицательное действительное число p₁, – вероятность реализации i‑го исхода бифуркационного события. При этом выполняется условие

В этом случае p₁, …, p_n суть вероятности элементарных исходов ω₁, …, ω_n или просто элементарные вероятности.

Каждому множеству A из ξ(Ω) поставлено в соответствие неотрицательное действительное число P(A). Это число называется вероятностью реализации совокупности исходов. Оно определяется как сумма вероятностей элементарных исходов, входящих в A:

где i_k – номера элементарных исходов, входящих в совокупность A_j.

Если P(A) > 0, то частное Р(В\А) = Р(АВ)/Р(А), где AB – пересечение множеств А и В, называется условной вероятностью реализации совокупности исходов В при условии реализации совокупности исходов. Отсюда непосредственно следует, что Р(АВ) = Р(В\А)Р(А).

Заключение по индукции даёт общую формулу Р(А₁А₂…А_n) = Р(А₁)Р(А₂\А₁)P(A₃\A₂\A₁₎…Р(А_n\А₁…А_n‑1) (теорема умножения).

Отсюда получаем Р(А\B) = Р(А)Р(В\А)/Р(B), и далее формулу полной вероятности Р(В) = P(A₁)P(B\A₁) + P(A₂)P(B\A₂) +…+ P(А_n)P(B\А_n),

где А₁+А₂+…+ А_n = Ω и В – произвольная совокупность исходов, и формулу Байеса:

Введение вектора α = {α₁}, где α_i=Υр_i, позволяет вместо некоторой аддитивной меры, рассматривать метрический вектор единичной длины в евклидовом пространстве. В этом случае вся изложенная выше теория может быть переформулирована в терминах амплитуды вероятности.

Каждому множеству А из ξ(Ω) может быть поставлено в соответствие неотрицательное действительное число Аp(А). Это число называется амплитудой вероятности реализации совокупности исходов А. Оно определяется как корень квадратный из суммы квадратов амплитуд вероятности элементарных исходов, входящих в А:

где i_k – номера элементарных исходов, входящих в совокупность А_j. Ар(Ω) = 1. Если А и B не пересекаются, то [Ap(A+B)]² =[Ар(А)]² + [Ар(В)]².

Каждому множеству А_j, состоящему из m_j элементарных исходов бифуркационного события, соответствует некоторый m_j‑мерный евклидов вектор Ар(А_j) = {a_jk} k = 1,…,m_j, модуль которого равняется

При этом разложение множества А_j на сумму взаимно не пересекающихся множеств эквивалентно разложению вектора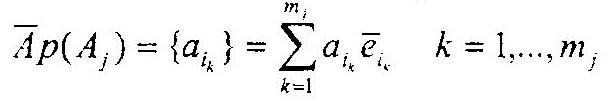

на сумму взаимно ортогональных векторов, каждый из которых имеет координаты, равные амплитудам элементарных событий, входящим в множество, которое он характеризует, е_j – орт координаты, характеризующей i‑й элементарный возможный исход бифуркационного события.

Формула Байеса переписывается в терминах амплитуды вероятностей следующим образом:

Дата добавления: 2019-02-12; просмотров: 203; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!