Глава 2. Теория функций комплексного переменного.
Действия над комплексными числами.
Задача 32. Возвести в степень 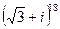 .
.
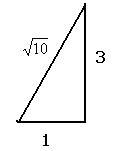
Решение. Чертёж:

Катеты имеют длину 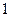 и
и 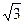 , поэтому в полярных коорданатах:
, поэтому в полярных коорданатах:
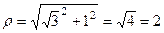 ,
, 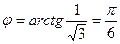 .
.
Тогда 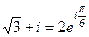 в показательной форме, а тогда
в показательной форме, а тогда 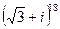 =
=

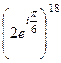 =
= 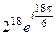 =
= 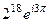 далее раскроем по формуле Эйлера:
далее раскроем по формуле Эйлера: 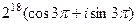 , но синус и косинус не зависят от добавления и вычитания полного оборота
, но синус и косинус не зависят от добавления и вычитания полного оборота 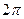 , поэтому получается
, поэтому получается 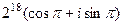 =
= 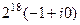 =
= 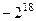 . Ответ.
. Ответ. 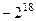 .
.
Задача 33. Вычислить в показательной форме 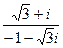 .
.
Решение.
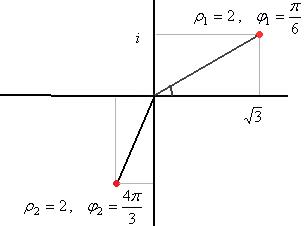
Для 1-го числа:  ,
,  (та же точка, как в прошлой задаче).
(та же точка, как в прошлой задаче).
Для 2-го числа: 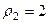 ,
, 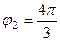 . Тогда
. Тогда 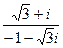 =
= 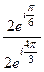 =
= 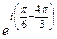 =
= 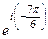 =
= 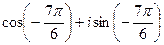 , прибавим
, прибавим 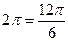 , для удобства вычисления. Итак,
, для удобства вычисления. Итак, 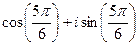 =
= 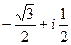 .
.
Ответ. 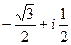 .
.
Задача 34. Вычислить 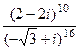 .
.
Решение. Представим в показательной форме каждое из чисел.
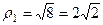 ,
, 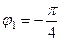 и
и 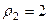 ,
, 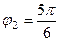 . Тогда
. Тогда
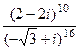 =
= 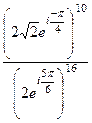 =
= 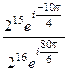 =
= 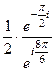 здесь в числителе прибавили угол
здесь в числителе прибавили угол 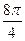 , кратный
, кратный 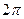 , а в знаменателе отняли
, а в знаменателе отняли 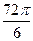 . Далее,
. Далее, 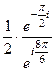 =
= 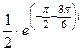 =
= 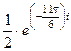 =
= 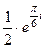 =
= 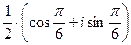 =
= 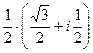 =
= 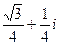 .
.
Ответ. 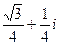 .
.
Домашняя задача. Вычислить 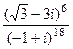 . Ответ.
. Ответ. 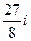
Задача 35. Вычислить 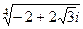
Решение. Формула:  .
.
Сначала найдём модуль и аргумент исходного числа.
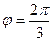 (т.к. 90 градусов и ещё 30 во второй четверти),
(т.к. 90 градусов и ещё 30 во второй четверти),
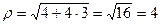 .
.
Тогда 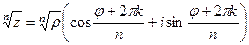 =
= 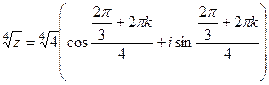 =
= 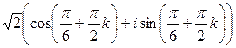 таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
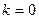 :
: 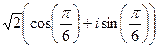 =
= 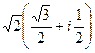 =
= 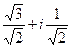 .
. 
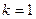 :
: 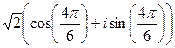 =
= 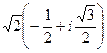 =
= 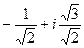 .
. 
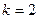 :
: 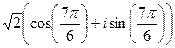 =
= 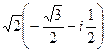 =
= 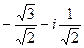 .
. 
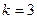 :
: 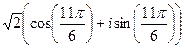 =
= 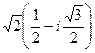 =
= 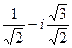 .
. 
Чертёж:
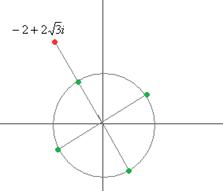
Ответ. 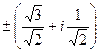 и
и 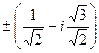 .
.
Задача 36. Дано 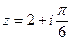 . Найти
. Найти 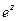 .
.
Решение. 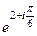 =
= 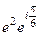 =
= 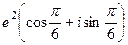 =
= 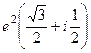 .
.
Ответ. 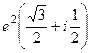 .
.
Задача 37. Дано 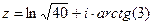 . Найти
. Найти 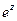 .
.
Решение. 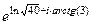 =
= 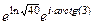 =
= 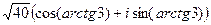 . Далее с помощью прямоугольного треугольника вычислим
. Далее с помощью прямоугольного треугольника вычислим 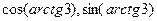 . Если надо найти синус и косинус того угла, тангенс которого равен 3, то сначала подпишем длины катетов по известному тангенсу, гипотенуза
. Если надо найти синус и косинус того угла, тангенс которого равен 3, то сначала подпишем длины катетов по известному тангенсу, гипотенуза 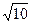 вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.
вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.
|
|
|
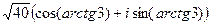 =
= 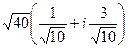 =
= 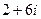 .
.
Ответ. 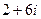 .
.
Задача 38. Дано 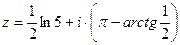 . Найти
. Найти  .
.
Решение. 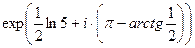 =
= 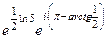 =
=
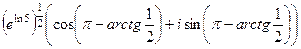 =
=
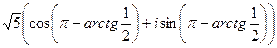 . Делаем аналогично тому, как в прошлой задаче, просто треугольник здесь во 2 четверти (угол
. Делаем аналогично тому, как в прошлой задаче, просто треугольник здесь во 2 четверти (угол 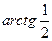 отмеряется от 180 в обратном направлении).
отмеряется от 180 в обратном направлении).
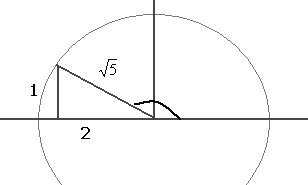
Но гипотенуза всё равно легко вычисляется по теореме Пифагора: 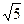 , тогда
, тогда 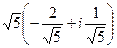 =
= 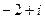 .
.
Ответ. 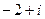 .
.
Задача 39. Найти все значения 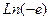 .
.
Решение. Используем формулу 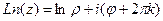 .
.
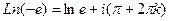 =
= 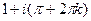 . Таким образом, это точки в комплексной плоскости, имеющие вид:
. Таким образом, это точки в комплексной плоскости, имеющие вид: 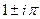 ,
, 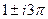 ,
, 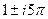 , ...
, ...
Ответ. 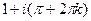 .
.
Задача 40. Найти все значения 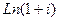 .
.
Решение. Используем формулу 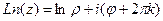 .
.
Для числа 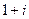 ,
, 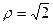 ,
, 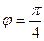 . Тогда
. Тогда
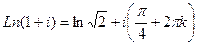 .
.
Чертёж: бесконечная последовательность точек, на уровне абсциссы
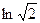 , по высоте каждая пара соседних отличается на
, по высоте каждая пара соседних отличается на 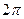 .
.
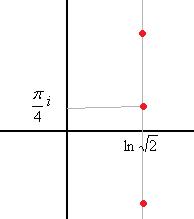
Ответ. 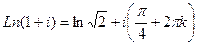 .
.
Динамическая анимация, показывающая поведение значений  в зависимости от колебаний модуля или аргумента
в зависимости от колебаний модуля или аргумента  , показана в следующем обучающем видеоролике:
, показана в следующем обучающем видеоролике:
http://www.youtube.com/watch?v=LKFFn-TSLd0
Практика № 6. 8 и 11.10.2018
Функции комплексного переменного
Задача 41. Вычислить 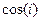 .
.
Решение. Применяем формулу 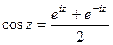 , где аргумент вместо
, где аргумент вместо 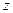 подставим
подставим 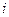 . Тогда
. Тогда 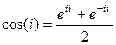 =
= 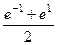 =
= 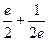 .
.
|
|
|
Ответ. 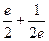 .
.
Заметим, что 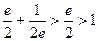 , то есть модули значений косинуса вне действительной оси не ограничены отрезком
, то есть модули значений косинуса вне действительной оси не ограничены отрезком 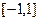 .
.
Задача 42. Решить уравнение  .
.
Решение. 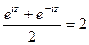
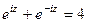
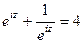 .
.
Введём замену 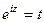 , при этом получаем
, при этом получаем
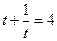
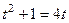
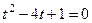 . Задача разбивается на 2 шага
. Задача разбивается на 2 шага
1) решим это уравнение и найдём 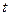 ,
,
2) учитывая 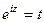 , запишем
, запишем 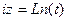 и далее найдём
и далее найдём 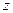 .
.
Квадратичное уравнение решаем через дискриминант, здесь 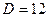 , тогда
, тогда 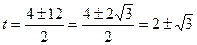 . Оба значения
. Оба значения 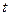 - положительные действительные числа, т.е. им соответствует аргумент
- положительные действительные числа, т.е. им соответствует аргумент 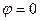 .
.
Далее, 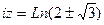
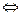
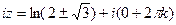
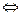
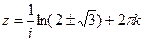
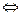
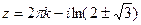 . Это две бесконечных последовательности точек, одна выше а другая ниже действительной прямой. По горизонтали расстояние между соседними ровно
. Это две бесконечных последовательности точек, одна выше а другая ниже действительной прямой. По горизонтали расстояние между соседними ровно 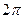 .
.
Чертёж:
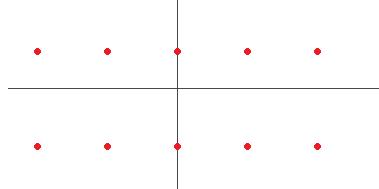
Замечание. Если число в правой части уменьшать до 1, то обе эти последовательности сближаются и в итоге соединятся в одну, расположенную на действительной прямой. Это будут в таком случае уже давно знакомые решения равенства 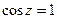 , т.е.
, т.е. 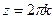 .
.
Общий случай. Если 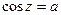 то
то 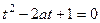 ,
, 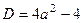 ,
, 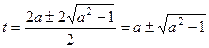 . Тогда
. Тогда 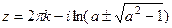 , что при
, что при 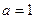 порождает
порождает 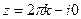 .
.
В следующей серии задач надо функцию представить в виде 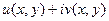 .
.
Задача 43. Функцию 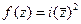 представить в виде
представить в виде 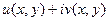 .
.
Решение. 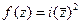 =
= 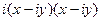 =
= 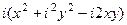 =
=
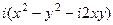 =
= 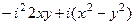 =
= 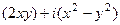 .
.
Поэтому 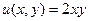 ,
, 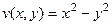 .
.
Заметим, что здесь нарушено уже даже 1-е условие Коши-Римана:
|
|
|
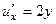 ,
, 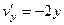 .
.
Ответ. 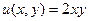 ,
, 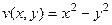 .
.
Задача 44. 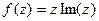 представить в виде
представить в виде 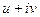 .
.
Решение. 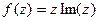 =
= 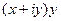 =
= 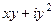
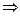
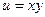 ,
, 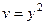 .
.
Заметим, что условия Коши-Римана не выполнены:
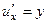 ,
, 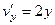 .
.
Ответ. 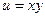 ,
, 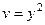 .
.
Задача 45. 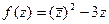 представить в виде
представить в виде 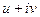 .
.
Решение. 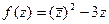 =
= 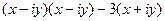
Раскроем скобки и перегруппируем слагаемые, чтобы сначала шли именно те, в которых нет мнимой единицы  , а затем те, в которых она есть.
, а затем те, в которых она есть.
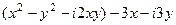 =
= 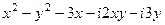 =
=
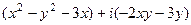
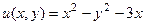 .
. 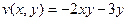 .
.
Ответ. 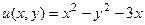 .
. 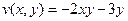 .
.
Задача 46. 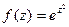 представить в виде
представить в виде 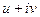 .
.
Решение. 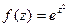 =
= 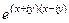 =
= 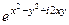 =
= 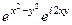
Далее по формуле Эйлера 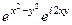 =
= 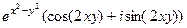 =
=
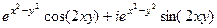 .
.
Ответ. 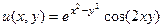 ,
, 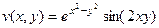 .
.
Задача 47. 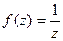 представить в виде
представить в виде 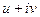 .
.
Решение. 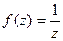 =
= 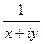 =
= 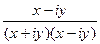
Домножили на сопряжённое, чтобы в знаменателе получилось некое единое действительное число, а разбиение на Re и Im осталось только в числителе. Тогда дробь можно будет разбить на сумму или разность двух дробей.
 =
= 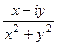 =
= 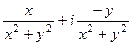 ,
,
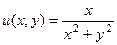 ,
, 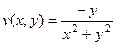 .
.
Ответ. 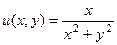 ,
, 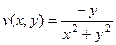 .
.
Задача 48. 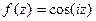 представить в виде
представить в виде 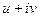 .
.
Решение. Если 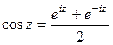 , то
, то 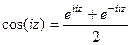 =
=
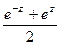 =
= 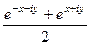 =
= 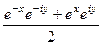
далее раскроем по формуле Эйлера:
... = 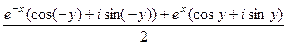 =
=
воспользуемся чётностью косинуса и нечётностью синуса:
... = 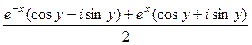 =
=
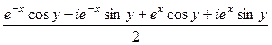 =
=
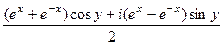 =
= 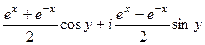 ,
,
это можно ещё записать в таком виде, используя гиперболические синус и косинус: 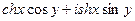 .
.
Ответ. 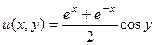 ,
, 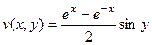 .
.
Задача 49. 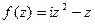 представить в виде
представить в виде 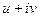 .
.
Решение. 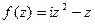 =
= 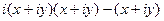 =
=
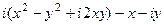 =
= 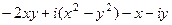 =
=
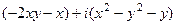 , тогда
, тогда
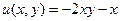 ,
, 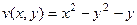 .
.
Ответ. 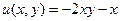 ,
, 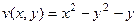 .
.
Задача 50. Для 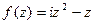 найти
найти 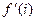 .
.
Решение.
Способ 1.
|
|
|
Производная как от единой функции 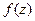 :
:
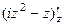 =
= 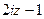 , что в точке
, что в точке 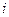 равно
равно 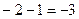 .
.
Способ 2.
По компонентам 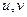 из предыдущей задачи:
из предыдущей задачи:
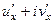 =
= 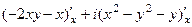 =
= 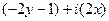 ,
,
в точке 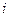 означает что в
означает что в 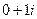 , т.е. данные функции надо вычислить в точке
, т.е. данные функции надо вычислить в точке 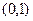 . Тогда
. Тогда 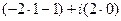 =
= 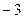 , как и том способе.
, как и том способе.
Ответ. 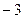 .
.
Дата добавления: 2019-01-14; просмотров: 154; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
