Криволинейные интегралы 1 рода
Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика
Курс практических занятий
Семестр 3
Учебное пособие
Для специальности
Информатика и вычислительная техника»
Томск
ТУСУР
2018
Электронное учебное пособие составлено и скорректировано с учётом реального проведения практических занятий на ФСУ в группах 437-1,2,3 осенью 2018 года. Даны с подробным разбором задачи, которые решались на каждом практическим занятии. Пособие может представлять методический интерес для преподавателей, работающих на аналогичных специальностях, как материал для планирования занятий. Применяется сквозная нумерация задач по всему семестру.
.
Оглавление
| ГЛАВА 1. Криволинейные, поверхностные интегралы. Теория поля........... Цилиндрические и сферические координаты................................ Криволинейные интегралы 1 рода ................................................. Поверхностные интегралы 1 рода .................................................. Криволинейные интегралы 2 рода ................................................. Поверхностные интегралы 2 рода .................................................. Потенциал векторного поля ............................................................ ГЛАВА 2. Теория функций комплексного переменного............. Действия над комплексными числами.......................................... Функции комплексного переменного ........................................... Восстановление аналитической функции по её действительной или мнимой части............................................................................ Интегрирование функций комплексного переменного................ Интегральная формула Коши.......................................................... | 5 5 13 16 18 25 31 35 35 42 46 51 56 |
|
|
|
Таблица соответствия дат и задач
| 437-1 | 437-2 | 437-3 | |
| дата задачи | дата задачи | дата задачи | |
| Практика 1 | 6.09 1 - 6 | 3.09 1 - 5 | 3.09 1 - 5 |
| Практика 2 | 13.09 7 - 12 | 10.09 6 - 12 | 10.09 6 - 12 |
| Практика 3 | 20.09 13 - 18 | 17.09 13 - 17 | 17.09 13 - 17 |
| Практика 4 | 27.09 19 - 23 | 24.09 18 - 25 | 24.09 18 - 25 |
| Практика 5 | 4.10 24 - 40 | 1.10 26 - 40 | 1.10 26 - 40 |
| Практика 6 | 11.10 41 - 52 | 8.10 41 - 52 | 8.10 41 - 52 |
| Практика 7 | 18.10 53 - 62 | 15.10 53 - 62 | 15.10 53 - 62 |
| Практика 8 | 25.10 63 - 68 | 22.10 63 - 68 | 22.10 63 - 68 |
| Практика 9 | 29.10 69 - 73 | 29.10 69 - 73 | 29.10 69 - 73 |
| Практика 10 | 12.11 | 12.11 | 12.11 |
| Практика 11 | 19.11 | 19.22 | 19.22 |
| Практика 12 | 26.11 | 26.22 | 26.22 |
| Практика 13 | 3.12 | 3.12 | 3.12 |
| Практика 14 | 10.12 | 10.12 | 10.12 |
| Практика 15 | 17.12 | 17.12 | 17.12 |
| Практика 16 | 24.12 | 24.12 | 24.12 |
Практика № 1.
Цилиндрические и сферические координаты
|
|
|
Задача 1. Найти объём тела, ограниченного поверхностями
 .
.
Решение. Построим плоский чертёж (вид сверху) рассматривая только те уравнения, которые не содержат  . Это позволит записать внешние интегралы по
. Это позволит записать внешние интегралы по  . Третий, внутренний, который по
. Третий, внутренний, который по  , в пределах от 0 до
, в пределах от 0 до  .
.


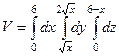 =
= 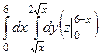 =
=  =
=
 =
=  =
=  =
=
 =
=  =
=  =
=
 =
=  =
=  =
=  =
=  . Ответ.
. Ответ.  .
.
Вспомним строение систем цилиндрических и сферических координат в пространстве и их определители Якоби.
Цилиндрические. 
 =
=  .
.
Сферические.  .
.  .
.
Задача 2. Вычислить тройной интеграл с помощью сферических координат: 
Решение. Чтобы перейти к новым координатам, рассмотрим, по какому трёхмерному телу ведётся интегрирование. Уравнение линии, которой достигает точка по  , имеет вид
, имеет вид  , что сводится к
, что сводится к  , то есть это окружность радиуса 1. Таким образом, при
, то есть это окружность радиуса 1. Таким образом, при  движемся вверх по
движемся вверх по  до окружности, то есть основание фигуры это четверть круга. Теперь рассмотрим, до куда точка движется по
до окружности, то есть основание фигуры это четверть круга. Теперь рассмотрим, до куда точка движется по  , в условии указано, что
, в условии указано, что  от 0 до
от 0 до  . Но уравнение
. Но уравнение  сводится к
сводится к  , т.е. это сфера радиуса 1. Таким образом, область интегрирования это 1/8 шара единичного радиуса в первом октанте, т.е. в той части пространства, где
, т.е. это сфера радиуса 1. Таким образом, область интегрирования это 1/8 шара единичного радиуса в первом октанте, т.е. в той части пространства, где  .
.
Пределы интегрирования таковы:  ,
,  ,
,  .
.
Пересчитаем подынтегральную функцию, чтобы выразить её через 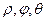 . В данном случае видим корень из суммы квадратов всех координат, поэтому сразу можно заметить, что по теореме Пифагора
. В данном случае видим корень из суммы квадратов всех координат, поэтому сразу можно заметить, что по теореме Пифагора  . Кроме того, умножим на определитель Якоби сферических координат, то есть
. Кроме того, умножим на определитель Якоби сферических координат, то есть  .
.
|
|
|
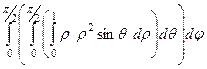 =
=  =
=
 =
= 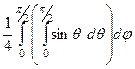 =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 3. Найти объём тела, ограниченного поверхностями:
 .
.
Решение. Основание фигуры - круг радиуса 1.

Тогда диапазоны изменения двух переменных: 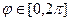 ,
,  , т.е. интеграл будет иметь вид
, т.е. интеграл будет иметь вид  , где нам осталось выяснить только диапазон изменения высоты в зависимости от положения точки в основании. В интеграле учтены при этом определитель Якоби
, где нам осталось выяснить только диапазон изменения высоты в зависимости от положения точки в основании. В интеграле учтены при этом определитель Якоби  и тождественная функция 1 (так как вычисляем объём). Далее,
и тождественная функция 1 (так как вычисляем объём). Далее,  , однако при этом надо выразить
, однако при этом надо выразить  через
через  , ведь во внешних интегралах зависимость именно от этих переменных. Тогда
, ведь во внешних интегралах зависимость именно от этих переменных. Тогда  .
.
 =
=  =
=  =
=  =
=  =
=
 =
=  =
=  =
=  .
.
Ответ.  .
.
Задача 4. Найти объём тела, ограниченного конусом
 и сферой радиуса
и сферой радиуса  , с помощью цилиндрических координат.
, с помощью цилиндрических координат.
Решение. Чертёж:

Это тело вращения с осью Oz. Проекцией на горизонтальную плоскость является круг радиуса 1. Тогда диапазоны изменения двух переменных очевидно таковы (как было для круга в полярных координатах): 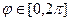 ,
, 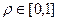 . Таким образом, нам остаётся только узнать диапазон изменения высоты в зависимости от расстояния до оси, то есть в зависимости от
. Таким образом, нам остаётся только узнать диапазон изменения высоты в зависимости от расстояния до оси, то есть в зависимости от  .
.
|
|
|
Построим сечение вертикальной плоскостью (вид сбоку).
По горизонтали - условная ось  , так как тело вращения и поэтому неважно, в какую сторону двигаться от оси, диапазон изменения высот ведёт себя одинаково на одном и том же расстоянии от оси вне зависимости от угла
, так как тело вращения и поэтому неважно, в какую сторону двигаться от оси, диапазон изменения высот ведёт себя одинаково на одном и том же расстоянии от оси вне зависимости от угла  .
.

Красным показана эта линия. Она проходит от прямой  до окружности радиуса
до окружности радиуса  , которую можно задать в виде
, которую можно задать в виде  .
.
Таким образом, надо вычислить интеграл  .
.
 =
= 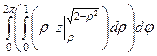 =
=  . Здесь далее можно рассматривать не как вложенные интегралы, а как произведение, т.к. интегрируя по
. Здесь далее можно рассматривать не как вложенные интегралы, а как произведение, т.к. интегрируя по  мы получим константу, и всё равно в итоге будет интеграл типа
мы получим константу, и всё равно в итоге будет интеграл типа  =
=  . Поэтому сразу запишем в виде
. Поэтому сразу запишем в виде  , далее
, далее
 =
=  =
=
 =
=  =
=
 =
=  =
=  =
=
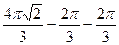 =
=  .
.
Ответ.  .
.
Задача 5. С помощью тройного интеграла вычислить объём 4-мерного шара, заданного уравнением  .
.
Решение. Выразим четвёртую координату через первые три:  . Область определения
. Область определения  явной функции - обычный 3-мерный шар радиуса R, а именно
явной функции - обычный 3-мерный шар радиуса R, а именно  .
.
Для нахождения указанного объёма нужно вычислить интеграл: 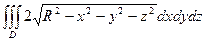 (аналогично тому, как для вычисления объёма трёхмерного шара вычисляли бы
(аналогично тому, как для вычисления объёма трёхмерного шара вычисляли бы  , где S - круг радиуса R). Вычисление тройного интеграла по
, где S - круг радиуса R). Вычисление тройного интеграла по  может быть выполнено с использованием сферических координат в трёхмерном пространстве.
может быть выполнено с использованием сферических координат в трёхмерном пространстве.
 =
= 
Интгерал по  вычисляется с помощью тригонометрической подстановки
вычисляется с помощью тригонометрической подстановки  .
.  =
=
 =
=
 =
=
 =
=  =
=
 =
=  =
=
 =
=  =
=  .
.
Ответ.  .
.
Задача 6. Вычислить тройной интеграл по 1/8 части шара в 1-м октанте от функции  .
.
Решение. Строение части шара такое же как в задаче 2. А вот в функции надо будет выразить всё через  по формулам сферических координат.
по формулам сферических координат.
 =
=
 далее, мы видим, что все множители зависят только от различных переменных, поэтому можно вынести их в соответствующий интеграл и считать не как вложенные действия, а как произведение.
далее, мы видим, что все множители зависят только от различных переменных, поэтому можно вынести их в соответствующий интеграл и считать не как вложенные действия, а как произведение.
 . Здесь в первом интеграле - подведение под знак дифференциала, во втором двукратно применим формулу понижения степени, а в третьем всё очевидно, там только степенная функция.
. Здесь в первом интеграле - подведение под знак дифференциала, во втором двукратно применим формулу понижения степени, а в третьем всё очевидно, там только степенная функция.
 =
=
 =
= 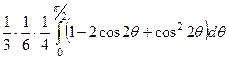 =
=
=  =
=  =
=  =
=
 =
=  . Ответ.
. Ответ.  .
.
Практика № 2.
Криволинейные интегралы 1 рода
Задача 7. Вычислить криволинейный интеграл 1 рода по окружности радиуса 1, на которой задана скалярная функция  .
.
Физический смысл. Можно представить таким образом: на проволоку, выполненную в виде окружности, напыляют какие-то частицы (тогда плотность вполне может даже обращаться в 0 в некоторых точках, ведь это плотность не самой проволоки, а напылённого вещества).
Решение. Вспомним основные формулы из лекций, для параметрически или явно заданной кривой в плоскости.
(1)  .
.
(2)  .
.
Решим эту задачу двумя способами, и увидим, что бывают ситуации, когда оба способа вполне применимы и уровню по сложности почти одинаковы.
Способ 1. Зададим окружность параметрически и воспользуемся первой формулой.  - параметрически заданное движение по окружности радиуса 1, где
- параметрически заданное движение по окружности радиуса 1, где  .
.
При этом  .
.  .
.
Тогда  =
=  =
=  =
=
 =
=  =
= 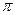 .
.
Способ 2. Зададим окружность явно и воспользуемся первой формулой. В данном случае  , из-за симметрии фигуры можно вычислить для верхней полуокружности и удвоить.
, из-за симметрии фигуры можно вычислить для верхней полуокружности и удвоить.
 , не зависит от
, не зависит от  , поэтому в ней не нужно пересчитывать
, поэтому в ней не нужно пересчитывать  через
через  . А в общем случае надо ещё и
. А в общем случае надо ещё и  - выразить только через
- выразить только через  . При этом
. При этом  .
.


 . Тогда 2
. Тогда 2  =
=  =
=  =
=  =
=  . Далее воспользуемся заменой (известной из 2-го семестра), с целью устранить корень.
. Далее воспользуемся заменой (известной из 2-го семестра), с целью устранить корень. 

 , при этом, чтобы не появлялся знак модуля, лучше даже свести всё к 1-й четверти, для этого можно воспользоваться тем фактом, что функция чётная, и записать интеграл так:
, при этом, чтобы не появлялся знак модуля, лучше даже свести всё к 1-й четверти, для этого можно воспользоваться тем фактом, что функция чётная, и записать интеграл так:  =
=  .
.
Если 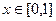 то соответственно
то соответственно  .
.
 =
=  =
=  =
=  =
=  =
=  =
=  =
= 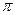 .
.
Ответ. 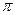 .
.
Задача 8. Вычислить массу проволоки, выполненной в виде графика  , плотность которой
, плотность которой  , где
, где  .
.
Решение. Здесь кривая задана явно, так что надо решать по формуле  . Очевидно,
. Очевидно, 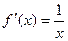 , тогда
, тогда
 =
= 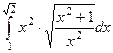 =
=  =
=  =
= 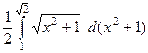 =
=  =
=
 =
=  .
.
Ответ. 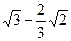 .
.
Задача 9. Найти криволинейный интеграл 1-го рода по винтовой линии (спирали) в пространстве, заданной параметрически:  , рассматривая 1 виток, т.е.
, рассматривая 1 виток, т.е.  ,
,
если скалярная функция  .
.
Решение. Нужно воспользоваться формулой для 3-мерного случая:
 .
.
Вычислим производные:  .
.
В функции  нужно все переменные полностью выразить через
нужно все переменные полностью выразить через  .
.
Получаем:  =
=
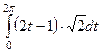 =
=  =
=  .
.
Ответ. 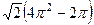 .
.
Дата добавления: 2019-01-14; просмотров: 263; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
