Поверхностные интегралы 2 рода (поток поля через поверхность).
Задача 18. Найти поток векторного поля 
через часть плоскости 
в 1-м октанте.
Решение. Данная поверхность это треугольник с вершинами (1,0,0), (0,1,0) и (0,0,1). При этом очевидно, что
, а также 
.
Воспользуемся формулой 
= 
. При этом ещё и повсеместно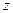 
представим в виде 
.
=
, где D - проекция исходного треугольника на плоскость, т.е. треугольник с вершинами (0,0), (1,0) и (0,1) в плоскости, ограниченный сверху линией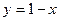 
(см. такой же треугольник в задаче 10).
Тогда = 
=
= 
=
= 
= 
=
= 
. Ответ. .
Аналогично прошлой задаче, но с другим векторным полем:
Задача домашняя Д-2. Найти поток векторного поля 
через поверхность в 1 октанте. Ответ. 
.
Задача 19. Найти поток векторного поля 
через поверхность 
, где 
.
Решение. Формула: = 
.
Здесь 
, 
.
= 
=
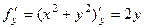, причём D это проекция параболоида на плоскость 0ху, то есть D круг радиуса 1. Делаем обычный переход к полярным координатам для такого круга, как в прошлом семестре.
= 
= 
= 
= 
.
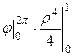Ответ. .
Ротор, дивергенция. Формулы Стокса, Остроградского-Гаусса и их применение.
Задача 20. Вычислить дивергенцию и ротор поля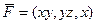 
.
Решение.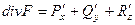 
= 
= 
.
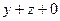rot(F) = 
= 
= 
.
Ответ. 
, 
.
Задача 21. Найти циркуляцию поля 
по треугольнику с вершинами (1,0,0), (0,1,0), (0,0,1).
Решение. Если вычислять без формулы Стокса, то надо найти 3 раза работу поля по 3 различным сторонам треугольника.
Например, можно на каждой стороне описать движение точки с помощью параметра 
так:
|
|
|
на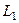 
: 
,
на 
: 
,
на 
: 
.
Но по формуле Стокса мы можем не делать 3 разных вычисления работы поля, а вычислить через двойной интеграл по единой области.
Формула Стокса. 
.
Для этого векторного поля, ротор был найден в задаче 20:
.
Нужно найти поток через данный треугольник, как в задаче 18, но не самого векторного поля, а ротора (нового векторного поля, полученного с помощью исходного).
Вычислим интеграл 
где
, 
, а 
это компоненты ротора, т.е. векторного поля ,
= 
=
= 
= 
=
= 
= 
= 
=
= 
= 
= 
.
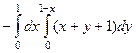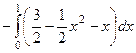Ответ. .
Задача 22. Найти поток поля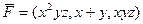 
через поверхность куба 
.
Решение. Если не использовать формулу Остроградского-Гаусса:
то нужно было бы вычислить 6 раз поток поля (через каждую грань поверхности куба). А по формуле Остроградского-Гаусса будет всего лишь одно вычисление тройного интеграла по внутренности куба.
Во-первых, 
.
Тогда 
= 
=
= 
= 
=
= 
= 
= 
. Ответ. .
Задача 23. Найти поток поля 
через поверхность, ограниченную эллиптическим параболоидом 
и плоскостью 
.
Решение.
Снова воспользуемся формулой Остроградского-Гаусса. Иначе пришлось бы вычислять 2 потока поля: по параболоиду и кругу.
Построим вертикальное сечение проходящее через ось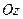 
, причём неважно, в какую сторону оно повёрнуто: для тела вращения, диапазон изменения 
зависит только от 
(расстояния от оси 
), но не зависит от угла 
. Поэтому так и обозначим оси: горизонтальную , вертикальную . Так как в сечении снизу парабола а сверху прямая линия на уровне 1, то 
. Проекция на горизонтальную плоскость - круг радиуса 1. Поэтому
|
|
|
. Обратите внимание, что 
мы тоже выразили в полярных координатах. Сначала применим формулу Ньютона-Лейбница по 
, получается:
= 
= 
, разобьём на 2 интеграла: здесь в первом слагаемом нет , а во втором есть, там можно будет вынести множитель, зависящий от .
=
во 2-м слагаемом по 
всё равно получается множитель 0, поэтому интеграл по можно и не вычислять.
= 
= 
.
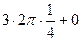Ответ. .
Потенциал векторного поля.
В следующих задачах найти потенциал, либо доказать, что поле не потенциально:
Задача 24. 
.
Решение.
Чтобы доказать, что поле потенциально, построим матрицу из всех 9 производных. В первом столбце по 
, во втором по 
и в 3-м по :
= 
Матрица симметрична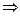 
поле потенциально.
Теперь ищем потенциал. Для этого соединим начальную точку с произвольной с помощью ломаной, чтобы каждое звено было параллельно какой-либо из осей координат.
|
|
|
Начальная точка, как правило, (0,0,0). Изменяющуюся переменную при этом будем обозначать через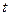 
, чтобы отличать от переменных , , , 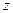которые в этих вычислениях будут использять роль верхнего предела в том или ином интеграле, либо роль фиксированной константы внутри функции. Получается такая сумма интегралов:
Применим это к конкретным функциям в этой задаче.
= 
= 
.
Вспомнив, что потенциал определяется с точность до константы, окончательный ответ можно записать так: 
.
Ответ. 
.
Задача 25. 
Решение. Найдём матрицу из всех производных:
= 
Матрица не симметрична. Тогда поле не потенциально.
Ответ. Поле не потенциально.
Задача 26. 
.
Решение. Найдём матрицу из всех производных:
= 
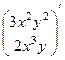Матрица симметрична. Поле потенциально.
Ищем криволинейный интеграл 2 рода по ломаной, соединяющей (0,0) с точкой 
.
= 
= 
= 
.
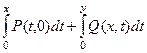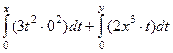Но потенциал вычисляется с точностью до константы, так что
.
Ответ. .
Проверка.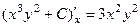 
, 
.
Задача 27. 
.
Решение. Найдём матрицу из всех производных:
= 
.
Матрица симметрична, значит, существует потенциал поля.
= 
= 
=
.
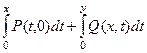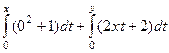Ответ. 
.
Проверка. 
, 
.
Задача 28. 
.
Решение. Найдём производную матрицу.
|
|
|
= 
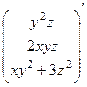Она симметрична, значит, поле потенциально. Ищем потенциал:
=
= 
= 
.
Ответ. 
.
Задача 29. 
.
Решение. Производная матрица симметрична:
= 
.
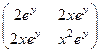Ищем потенциал поля.
= 
= 
=
= 
= 
.
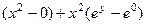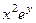Ответ. 
Задача 30. 
.
Решение. 
= 
симметрична.
= 
= 
= 
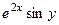. Ответ. 
.
Задача 31. 
.
Решение. 
= 
симметрична.
В данном случае мы не можем в качестве начальной точки взять (0,0,0), так как эти функции имеют там бесконечный предел. Однако можно рассматривать точку (1,1,1) .
= 
=
= 
=
= 
.
Ответ. 
.
Дата добавления: 2019-01-14; просмотров: 518; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!