Преобразование метрической шкалы в нормированную
В ряде случаев задание нуля на единой метрической шкале производят на основе нормативной выборки испытуемых. Для этого используют следующую методику:
1) усредняют с учетом среднеквадратичных ошибок все значения уровней подготовленности испытуемых 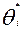 , попавших в нормативную выборку, и получают средневзвешенное значение
, попавших в нормативную выборку, и получают средневзвешенное значение 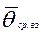 ;
;
2) рассчитывают соответствующую дисперсию уровня подготовленности участников из нормативной выборки относительно 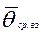 ;
;
3) смещают оценки всех латентных параметров на величину 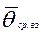 , полученные значения
, полученные значения  и
и  являются окончательными оценками соответствующих латентных параметров на единой метрической шкале, а начало этой шкалы определяется нормативной выборкой.
являются окончательными оценками соответствующих латентных параметров на единой метрической шкале, а начало этой шкалы определяется нормативной выборкой.
Объем  нормативной выборки выбирают таким образом, чтобы среднеквадратичная ошибка величины
нормативной выборки выбирают таким образом, чтобы среднеквадратичная ошибка величины  была бы примерно в 5 раз меньше среднеквадратичных ошибок оценок
была бы примерно в 5 раз меньше среднеквадратичных ошибок оценок  , т.к. величина
, т.к. величина  в среднем также в 5 раз меньше величины
в среднем также в 5 раз меньше величины  , то желательно, чтобы объем выборки составлял бы не менее 625 участников.
, то желательно, чтобы объем выборки составлял бы не менее 625 участников.
Увеличение дифференциации результатов тестирования
При работе с достаточно большими выборками испытуемых проблема дифференциации результатов тестирования становится невероятно острой. Поскольку статистические оценки уровней подготовленности всех участников, набравших одинаковые первичные баллы, будут совпадать, т.к. являются равными функциями равных достаточных статистик (по крайней мере, в рамках модели Раша). Например, если в тесте 40 заданий, то вне зависимости от общего количества участников и вне зависимости от используемой шкалы количество различных значений окончательного балла не может превышать 40. Для повышения степени дифференциации можно учитывать еще и уровень трудности заданий, и коэффициенты дискриминации (разрешающей способности) заданий [6]. Одним из путей решения этой проблемы является дополнительное использование и окончательных баллов  заданий вариантов теста для использования их в качестве весовых коэффициентов. Это позволяет дополнительно дифференцировать участников, набравших один и тот же балл, в зависимости от суммы баллов верно выполненных ими заданий. Пусть
заданий вариантов теста для использования их в качестве весовых коэффициентов. Это позволяет дополнительно дифференцировать участников, набравших один и тот же балл, в зависимости от суммы баллов верно выполненных ими заданий. Пусть  - окончательный балл испытуемых, набравших один и тот же первичный балл b, а
- окончательный балл испытуемых, набравших один и тот же первичный балл b, а  - количество таких испытуемых. Каждому b=1, 2, 3, ……К-1 соответствует список участников тестирования, пронумерованный в порядке возрастания суммы баллов верно выполненных ими заданий. Участники, выполнившие наиболее легкие задания, будут находиться в начале списка, наиболее трудные в конце. Весь список из
- количество таких испытуемых. Каждому b=1, 2, 3, ……К-1 соответствует список участников тестирования, пронумерованный в порядке возрастания суммы баллов верно выполненных ими заданий. Участники, выполнившие наиболее легкие задания, будут находиться в начале списка, наиболее трудные в конце. Весь список из 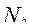 участников соответствует одной точке
участников соответствует одной точке  метрической шкалы и необходимо распределить испытуемых по целым числам из промежутка:
метрической шкалы и необходимо распределить испытуемых по целым числам из промежутка:
|
|
|
|
|
|
 .
.
Распределение по целым числам из указанного промежутка необходимо выполнить в соответствии с распределением реально полученных значений  ,
, 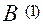 ,
, 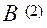 , ……,
, ……,  . При использовании 100 балльной шкалы,
. При использовании 100 балльной шкалы,  =0, а
=0, а  =100. Если распределение реально полученных значений
=100. Если распределение реально полученных значений  ,
,  ,
, 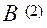 , ……,
, ……,  непринципиально отличается от нормального закона, то можно использовать модельную плотность вероятности вида [13]:
непринципиально отличается от нормального закона, то можно использовать модельную плотность вероятности вида [13]:
 ,
,
являющуюся частичной суммой ряда Грамма - Шарлье для плотности нормального закона распределения, где  центрированная и нормированная переменная
центрированная и нормированная переменная  ,
,  - математическое ожидание,
- математическое ожидание,  - стандарт, asim- асимметрия (скос), eks- эксцесс распределения баллов B.
- стандарт, asim- асимметрия (скос), eks- эксцесс распределения баллов B.
 ,
,
 ,
,
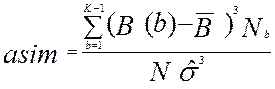 ,
,
 ,
,
 ,
,  .
.
Список состоящий из  человек, надо разделить на
человек, надо разделить на  групп пропорционально числам
групп пропорционально числам  (
( 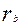 -количество целых чисел
-количество целых чисел  на промежутке
на промежутке  ),
),  - вероятность попадания случайной величины B в единичную окрестность целого числа
- вероятность попадания случайной величины B в единичную окрестность целого числа  :
:
 ,
,  ,
, 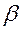 = 2, 3, …….,
= 2, 3, ……., 
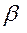 - номер целого числа
- номер целого числа  , такой, что большему числу
, такой, что большему числу  соответствует и больший номер
соответствует и больший номер 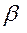 . Для крайних точек
. Для крайних точек  и
и  вероятности
вероятности  следует считать по формуле:
следует считать по формуле:
|
|
|
 ,
,  ,
,  или
или  .
.
Первая группа участников тестирования будет состоять из  человек, а их окончательный балл будет равен целому числу
человек, а их окончательный балл будет равен целому числу  из промежутка
из промежутка  . Вторая группа будет состоять из
. Вторая группа будет состоять из  человек с окончательным баллом
человек с окончательным баллом  и т.д. до
и т.д. до  .
.
В заключении следует отметить, что наибольшие изменения будут претерпевать баллы, находящиеся в средней части метрической шкалы, а высокие и низкие значения баллов будут изменяться незначительно.
IRT - теория моделирования и параметризации педагогических тестов
Другой наиболее широко используемой моделью диагностики знаний в настоящее время является двухпараметрическая модель Бирнбаума [30,31], относящаяся к теории моделирования и параметризации педагогических тестов или сокращенно ТМППТ. В англоязычной литературе данная теория носит название Item Response Theory (IRT). Принципиальное отличие Item Response Theory от теории Раша заключается в том, что в данном случае каждое тестовое задание рассматривается, как самостоятельная структурная единица, параметры которой не зависят от параметров других заданий.
В основе всех моделей Item Response Theory лежат так называемые функции успеха, имеющие заранее известный вид и определяющие зависимость верного решения задания от уровня подготовленности испытуемого. Для оценки параметров моделей Item Response Theory используют специальные итерационные методы, что является достаточно сложной задачей, однако эти модели имеют по сравнению с моделью Раша ряд преимуществ. В частности, для нанесения результатов на единую шкалу по различным вариантам теста нет необходимости вводить предположения об их параллельности. Более того, можно свести воедино результаты, полученные при использовании разных по трудности тестов. Модели Item Response Theory менее чувствительны к длине теста и уровню трудности заданий. Следует отметить, что дисперсия ошибки измерения уровня подготовленности в модели Раша несколько больше, чем в Item Response Theory.
|
|
|
Одной из основных и наиболее применимых моделей Item Response Theory является так называемая двухпараметрическая модель Бирнбаума. Сущность этой теории заключается в следующем [27,28]. Пусть параметр 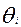 отражает уровень подготовленности i- участника испытаний, а параметры
отражает уровень подготовленности i- участника испытаний, а параметры 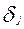 и
и 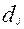 - некоторые параметры j- тестового задания (
- некоторые параметры j- тестового задания ( 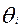 и
и 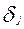 - любые числа, а
- любые числа, а 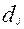 - только положительные). Согласно модели Бирнбаума вероятность (
- только положительные). Согласно модели Бирнбаума вероятность (  ) успешного выполнения j- задания, i-участником определяется следующей формулой:
) успешного выполнения j- задания, i-участником определяется следующей формулой:
 .
.
Данное выражение показывает, что вероятность успеха  зависит только от
зависит только от 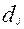 и
и  поэтому модель Бирнбаума, получила название двухпараметрической. Вероятность успеха
поэтому модель Бирнбаума, получила название двухпараметрической. Вероятность успеха  как функция от
как функция от 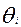 при фиксированных значениях
при фиксированных значениях  и
и  называется характеристической функцией j – задания. На рисунке 3 представлен вид характеристической кривой с параметрами
называется характеристической функцией j – задания. На рисунке 3 представлен вид характеристической кривой с параметрами  и
и  . Исследование характеристических функций показывает, что:
. Исследование характеристических функций показывает, что:
 и
и  ,
,
т.е. с уменьшением уровня подготовленности участника вероятность верного решения задания уменьшается до 0, а при увеличении уровня подготовленности увеличивается до 1.

Рис.3. Характеристическая кривая задания с уровнем трудности  и различающей (дифференцирующей) способностью
и различающей (дифференцирующей) способностью  .
.
При увеличении параметра  , характеризующего трудность задания, вероятность успеха для одного и того же уровня подготовленности уменьшается. При небольших значениях параметра
, характеризующего трудность задания, вероятность успеха для одного и того же уровня подготовленности уменьшается. При небольших значениях параметра 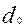 характеристическая кривая является пологой, следовательно, для испытуемых с уровнем подготовленности
характеристическая кривая является пологой, следовательно, для испытуемых с уровнем подготовленности 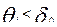 и для участников тестирования с
и для участников тестирования с  вероятности верного решения данного задания приблизительно равны. Если значение параметра
вероятности верного решения данного задания приблизительно равны. Если значение параметра  велико, то вероятности успеха будут существенно различаться, поэтому параметр
велико, то вероятности успеха будут существенно различаться, поэтому параметр 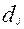 получил название коэффициента дискриминации. Этот коэффициент показывает насколько данное задание, хорошо различает участников тестирования с высоким, и низким уровнем подготовленности. На рис.4 изображены характеристические кривые для заданий с одинаковыми параметрами трудности
получил название коэффициента дискриминации. Этот коэффициент показывает насколько данное задание, хорошо различает участников тестирования с высоким, и низким уровнем подготовленности. На рис.4 изображены характеристические кривые для заданий с одинаковыми параметрами трудности  , но с разными коэффициентами дискриминации
, но с разными коэффициентами дискриминации  и
и 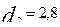 . Характеристическая кривая, изображенная сплошной линией, соответствует заданию с коэффициентом дискриминации
. Характеристическая кривая, изображенная сплошной линией, соответствует заданию с коэффициентом дискриминации  , а пунктиром заданию с
, а пунктиром заданию с 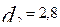 . Рассмотрим точку
. Рассмотрим точку  на оси
на оси  , из графика видно, что для кривой с
, из графика видно, что для кривой с  вероятности выполнения задания участниками с уровнями подготовленности
вероятности выполнения задания участниками с уровнями подготовленности  и с
и с  различаются несущественно. Для
различаются несущественно. Для 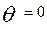 , соответствующая вероятность успеха равна 0,43 , а для
, соответствующая вероятность успеха равна 0,43 , а для  , соответствующая вероятность равна 0,57. Для характеристической кривой задания с
, соответствующая вероятность равна 0,57. Для характеристической кривой задания с  вероятность выполнения задания участниками тестирования с уровнями подготовленности
вероятность выполнения задания участниками тестирования с уровнями подготовленности  и с
и с 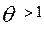 различаются существенно. Для
различаются существенно. Для 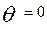 , соответствующая вероятность успеха равна 0,06 , а для
, соответствующая вероятность успеха равна 0,06 , а для  , соответствующая вероятность равна 0,94.
, соответствующая вероятность равна 0,94.

Рис.4. Характеристические кривые задания с одинаковым уровнем трудности  и с разными коэффициентами дискриминации
и с разными коэффициентами дискриминации 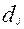
Дата добавления: 2019-01-14; просмотров: 220; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
