Использование достаточных статистик
В рамках модели Раша первичные баллы участников тестирования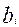 
(i=1, 2, 3, ……N) и заданий 
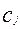являются достаточными статистиками. Поэтому, если варианты теста являются параллельными, то участники, набравшие одинаковые первичные баллы получат одинаковые оценки подготовленности 
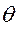в логитах. Это позволяет получить на единой метрической шкале в логитах (К-1) узловых точек [6]:
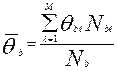, b=1, 2, 3, …., К-1,
где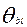 
- уровень подготовленности участников, выполнявших 
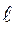вариант теста и набравших b баллов, 
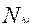- количество таких участников ( 
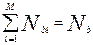- общее число участников по всем вариантам, набравшим по b баллов). Обозначим через 
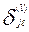уровень трудности j- узлового задания, полученный при обработке матрицы ответов 
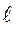- го варианта. Тогда для сведения всех уровней подготовленности, полученных по всем параллельным вариантам теста к единой метрической шкале можно использовать следующий алгоритм:
с помощью критерия согласия необходимо проверить статистические гипотезы о возможности применения модели Раша для описания полученных экспериментальных результатов;
необходимо задать условное начало (ноль) метрической шкалы для всех вариантов. Для чего из всех оценок латентных параметров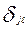 
и 
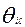вычитается значение 
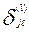. Если бы модель Раша была бы полностью адекватна результатам тестирования, и отсутствовали бы ошибки измерений, то указанные смещения привели бы к полному совпадению значений 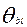, соответствующих одному и тому же значению первичного балла для любых вариантов теста, что является на практике маловероятным;
необходимо усреднить оценки подготовленности 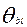, соответствующие одинаковому первичному баллу b по различным вариантам теста и подсчитать дисперсии значений 
( 
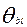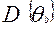). Для одного (любого) варианта и дисперсию усредненного значения 
( 
):
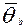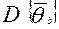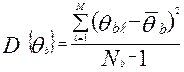, b=1, 2, 3, …… К-1,
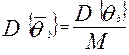
Однако необходимо убедиться, что максимальное уклонение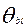 
от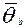 
не противоречит гипотезе о равенстве математических ожиданий 
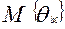для любых параллельных вариантов теста.
Числа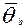 
делят метрическую шкалу в логитах на К промежутков, каждому из которых можно приписать номер от 1 до К. Чтобы перенести на единую метрическую шкалу трудность 
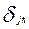j – задания (j=1, 2, 3, ….. К) в 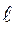- варианте ( 
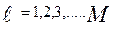), попадающую на промежуток с определенным номером, необходимо сделать линейную интерполяцию:
,
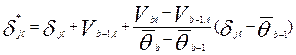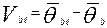и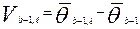 
- уклонения реально полученных оценок уровня подготовленности в 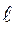варианте от усредненных значений, 
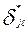- исправленная трудность.
Недостатком данного подхода является то, что при линейной интерполяции копируется погрешность узловых значений уровней трудности заданий. Необходимо сглаживать эту погрешность, например можно аппроксимировать каждую функцию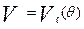 
, заданную дискретно в (К-1) точках 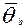, кубическим сплайном 
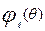(с учетом точности характеристик исходных значений 
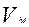) [29]. Тогда исправленное значение латентного параметра уровня трудности задания можно представить следующим образом:
.
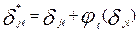Далее используя исправленные значения уровней подготовленности участников тестирования (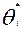 
), приведенные к единой метрической шкале можно определить их окончательный балл.
Дата добавления: 2019-01-14; просмотров: 167; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!