Дробная и политомическая оценка результатов тестирования
Введение дробной оценки результатов тестирования является весьма продуктивным и интересным, поскольку позволяет провести более селективное распределение участников тестирования по баллам, чем использование целочисленных шкал, в которых число возможных значений рейтинга равно максимальному баллу.
Простая алгебраическая модель оценивания результатов тестирования [19,20] предполагает, что каждое из заданий может быть оценено в некоторой дробной шкале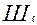 
имеющей следующий вид:
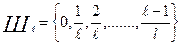, где 
.
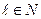Необходимо ввести некоторые обозначения:
N-число участников тестирования;
К-количество заданий в тесте;
Пусть в результате тестирования получена матрица первичных баллов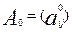 
( 
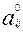первичный балл i-участника за j –задание, соответственно равный 1, если задание выполнено верно, и 0, если задание выполнено неправильно). Введем дополнительно следующие параметры:
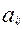- степень решенности j – задания i – участником (в дробной шкале );
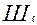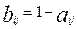степень нерешенности j – задания i – участником (в дробной шкале 
);
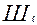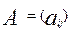матрица результатов тестирования в дробной шкале 
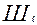, размера 
;
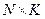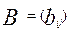- матрица размера 
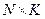, двойственная к матрице результатов тестирования 
;
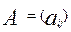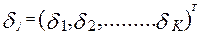- вектор столбец трудности заданий;
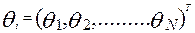- вектор столбец уровней подготовленности тестируемых.
Модель дробной оценки результатов тестирования основывается на следующих предположениях:
трудность заданий является экспериментально определяемой величиной;
|
|
|
окончательный (сертификационный) балл (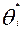 
) i -участника определяется как сумма основного балла (за “широту” знаний) ( 
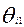) и призового (за “глубину”) ( 
) 
;
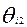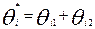основной балл тестируемого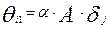 
, где α > 0 некоторая константа;
трудность заданий теста пропорциональна сумме ненабранных на этом задании тестовых баллов с учетом основных баллов испытуемых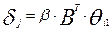 
, β>0;
призовой балл тестируемого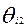 
пропорционален количеству полностью решенных им заданий: 
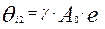, где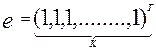 
, γ>0.
На основании изложенных предположений для вектора – столбца трудности заданий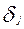 
можно записать:
,
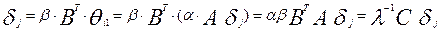где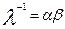 
, 
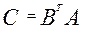- квадратная матрица К – ого порядка.
Вектор – столбец трудности заданий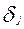 
является неотрицательным правым собственным вектором матрицы 
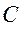, соответствующим положительному собственному значению λ. Неотрицательный правый собственный вектор ( 
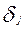) матрицы 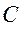и его собственное значение λ могут быть найдены после обработки результатов тестирования. Если для оценки трудности заданий ввести R –бальную шкалу, то вектор трудности заданий в такой шкале рассчитывается по формуле:
,
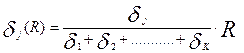основной балл (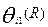 
, α=1/2):
,
|
|
|
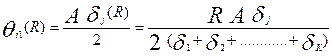призовой балл (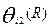 
, γ=1/2):
,
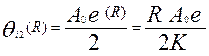для окончательного (сертификационного) балла ( 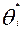) получим:
.
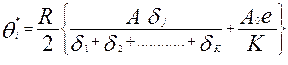Близкий по идеологии подход может быть реализован, если оценивать выполнение не всего тестового задания в целом (0 или 1), а результат выполнения каждого шага j –задания i –участником тестирования дихотомической оценкой. При этом все задание получит политомическую оценку, величина которой будет находиться в интервале от 0 до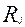 
, где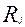 
- количество шагов в j- задании теста [21]. Таким образом, если учитывать степень трудности каждого шага результаты тестирования N –участников с помощью K – заданий, каждое из которых состоит из 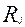- шагов, будут представлять 3-х мерную матрицу, состоящую из N- строк, К – столбцов и 
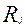- “подстолбцов”. Однако, если трудность каждого шага выполнения заданий не учитывать, то получится матрица результатов в которой, для каждого участника будет свое (целое) количество баллов за каждое задание. Такая матрица ответов может быть обработана исходя из любой существующей модели тестирования.
Однако, наиболее адекватные результаты, в случае политомической оценки заданий, дает модель Partial Credit [22-24]. Которую можно рассматривать как обобщение модели Раша. Элементы матрицы ответов при тестировании с использованием политомически оцениваемых заданий принимают значения от 0 до 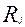(где 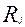- максимальный балл за j- задание) и являются случайными величинами. Можно выбрать одно, какое либо задания j и проверить адекватность модели Partial Credit для экспериментально полученных результатов. Если 
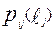вероятность получения i –участником тестирования 
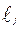- баллов за j –задание, то математическое ожидание балла 
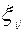- полученного i –участником тестирования за данное задание –j определяется по следующей формуле:
|
|
|
,
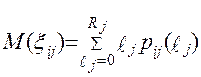а дисперсия величины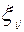 
:
.
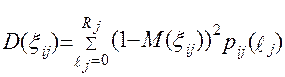Математическое ожидание и дисперсия величины 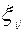позволяют проверить адекватность модели Partial Credit с помощью критерия χ2 –Пирсона. Для этого необходимо найти случайную величину 
:
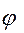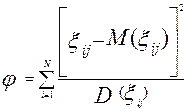
Если модель Partial Credit является адекватной полученным при тестировании данным (для данного задания j), то величина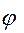 
подчиняется распределению 
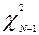(с N-1 степенью свободы). Для более точной оценки возможности применения модели Partial Credit необходимо использовать несколько различных заданий теста. Проверка данной модели, проведенная Центром тестирования Министерства образования РФ показала, что она является достаточно адекватной для обработки результатов тестирования с политомически оцениваемыми заданиями.
|
|
|
Нормативная шкала
Более приемлемыми для оценки достижений учащихся являются нормативные шкалы. Нормативная шкала разрабатывается на основе предположения о нормальном законе распределения баллов. Одной из причин применения нормативной шкалы является то, что линейная трансформация первичных (необработанных) баллов зависит от характеристик заданий в тесте. Перевод в нормативную шкалу предполагает, что знания испытуемых в их произвольной выборке подчиняются нормальному закону распределения, и равные отрезки под кривой распределения соответствуют равному количеству правильных ответов. При данном подходе используется следующая процедура. Сначала, на случайной выборке из генеральной совокупности проводится тест. Далее строится распределение первичных баллов, при этом стараются добиться их нормального распределения. Соответствие закона распределения экспериментально полученных первичных баллов нормальному закону распределения можно проверить методами статистической проверки гипотез распределения. В данном случае окончательный балл выставляется в зависимости от относительных успехов данного испытуемого в сравнении с остальными участниками. В результате тестирования получается экспериментальная функция распределения (F(x)) вероятности (p(x)) наблюдения тех или иных первичных баллов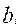 
. Далее необходимо определить число интервалов, на которые делится числовая прямая, определяющая оценку. Если деление происходит на 2 промежутка, соответствующих оценкам: ”зачет - незачет”, то находится 50 ая процентиль, называемая медианой. Если осуществляется деление на 5 интервалов (что соответствует оценкам: 1, 2, 3, 4, 5), то необходимо определить соответствующие пентели (4 индекса делят числовую прямую на 5 частей) и т.д. Характер частотного распределения первичных баллов [25,26] отражается на значениях соответствующих процентилей и поэтому, например, пентили можно использовать в качестве окончательной оценки балла по 5 балльной шкале, децили по 10-ти балльной, центили по 100 бальной и т.д. В таком случае балл 
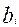участника с номером i выражает процентную долю испытуемых, первичный балл которых ниже первичного балла 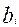данного испытуемого. Подобные шкалы называют процентильными или шкалами первичных процентилей. Эти шкалы, как и шкала процентов, имеют ранговый смысл и поэтому их трудно сравнивать между собой, если они получены по разным выборкам. Стандартизация достигается путем преобразования всех экспериментальных функций плотности распределения баллов к нормальному закону. Для нормального закона распределения медиана совпадает с математическим ожиданием. Расстояние между нижней 
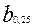и верхней 
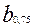квартилями равно 0,675σ а соответствующая р-ая квантиль определяется по формуле:
.
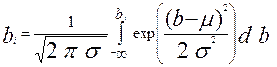Если получаемое экспериментально распределение баллов отличается от нормального закона распределения, то его подвергают принудительной нормализации [53], однако отклонение от нормального закона говорит об неудачно подобранных тестовых заданиях. Если принудительной нормализации не требуется, то достаточно выполнить центрирование и нормирование экспериментально полученного распределения первичных баллов по формуле:
,
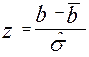где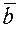 
- математическое ожидание, а 
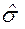- среднеквадратичное отклонение, 
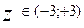. Полученные значения Z не являются удобными для использования в качестве баллов, однако их можно преобразовать в более наглядный вид, чтобы избавится от отрицательных баллов и изменить единицы измерения. Для чего можно использовать например следующую формулу:
,
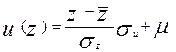где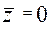 
, 
, 
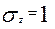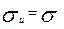. Характеристикой точности измерения индивидуального балла служит среднеквадратичная оценка 
:
,
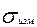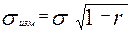где r- коэффициент надежности теста.
На основании первичного балла возможно построение следующих нормативных шкал:
-процентная шкала (выставляемый балл прямо пропорционален первичному баллу);
-шкала первичных процентилей (выставляемый балл соответствует квантилям экспериментально полученного распределения частот первичных баллов);
-нормализованные шкалы (экспериментально полученное распределение первичных баллов подвергается нормализации и преобразованию к модельному распределению вида );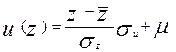
-шкалы нормализованных процентилей (выставляемый балл соответствует квантилям модельного распределения вида
);
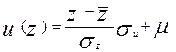-нормализованные шкалы с постоянным шагом (индексы шкалы выставляемого балла соответствуют равноудаленным значениям стандартной переменной Z).
При оценивании результатов с использованием нормативной шкалы в ряде случаев целесообразно использовать задания с заранее известным распределением уровней трудности, отличным от нормального закона. Например, при аттестационном тестировании предпочтительнее, чтобы распределение трудности заданий имело “крутое левое крыло” и растянутое “правое крыло” (см. рис.2). Данный характер распределения может быть обеспечен за счет повышения доли простых заданий (и/или повышении оценок простых заданий) в тесте, чего можно добиться предварительной нормировкой.
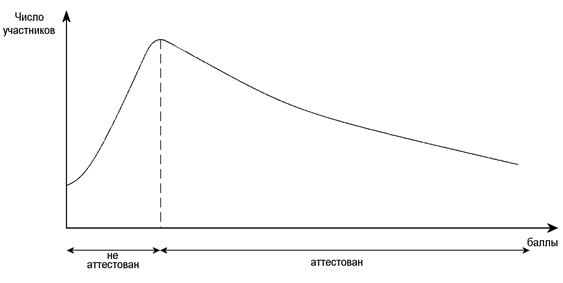
Рис.2. Кривая распределения результатов аттестационного тестирования с растянутым “правым крылом”
Метрическая шкала
Основным достоинством теории Раша является возможность построить не порядковую, а метрическую шкалу выставляемых баллов, т.е. произвести измерение уровня их подготовленности, а не ранжирование участников [6,27,28].
Пусть имеется матрица ответов N участников тестирования на К заданий теста, и полученные результаты полностью описываются моделью Раша. Тогда пересчет окончательного балла в 100 бальную шкалу можно осуществить линейным преобразованием, например, приравняв самый маленький уровень подготовленности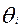 
нулю, а самый большой 
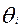- 100 баллам. Кроме того, можно пойти следующим путем:
,
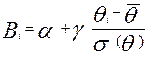где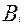 
- окончательный тестовый балл на 100 бальной шкале, 
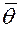- среднее значение уровня подготовленности, 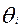- уровень подготовленности i – участника, 
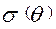- среднеквадратичное отклонение, 
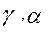- некоторые эмпирические коэффициенты подбираемые вручную (например 
, 
).
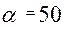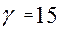Дата добавления: 2019-01-14; просмотров: 806; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!