Использование монотонности функции
Пусть на промежутке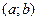 
задана возрастающая функция 
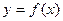и требуется решить неравенство 
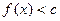(или 
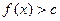). Если 
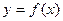– корень уравнения , причем 
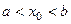, то решения данного неравенства – весь промежуток 
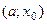(соответственно промежуток 
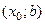). Единственность корня следует из монотонности 
. Понятно, что если требуется решить нестрогое неравенство, то при том же рассуждении в ответ войдет и число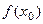 
, а если функция задана на замкнутом или полуоткрытом промежутке, то в ответ войдут соответствующие концы промежутка.
Пример 30. Решить неравенство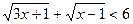 
.
Решение: Заметим, что левая часть данного неравенства – возрастающая функция (обозначим ее через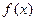 
). При 
левая часть равна правой. Учтем ОДЗ исходного неравенства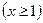 
и рассмотрим его на промежутке 
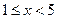. Имеем 
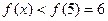, то есть данное неравенство выполняется. При 
по той же причине (из-за возрастания функции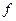 
) 
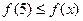, то есть данное неравенство не выполняется. Так как исследование проведено при всех допустимых значениях 
, решение закончено.
Ответ: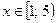 
Использование ОДЗ
Пример 31. Решить неравенство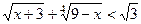 
.
Решение:ОДЗ этого неравенства есть все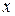 
из промежутка 
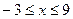. Разобьем это множество на два промежутка 
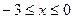и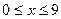 
.
Для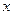 
из промежутка 
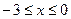имеем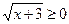 
, 
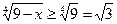. Следовательно, 
на этом промежутке, и поэтому исходное неравенство не имеет решений на этом промежутке.
Пусть 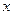принадлежит промежутку 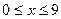, тогда 
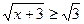и 
. Следовательно, 
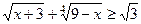для таких 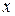, и, значит, на этом промежутке исходное неравенство также не имеет решений.
Ответ: решений нет.
Пример 32. Решите уравнение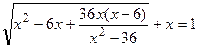 
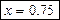
Решение. Преобразуем подкоренное выражение
.
ОДЗ: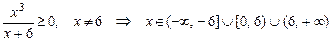 
. Уравнение принимает вид
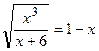. Оно имеет решение только, если 
. Возведем в квадрат 
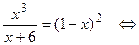
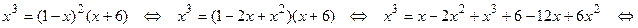
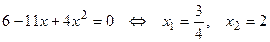. Второй корень не удовлетворяет условию 
.
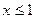Пример 33. Решить неравенство 
Решение. Найдем ОДЗ: 
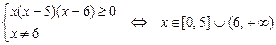. 1) Если 
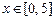, то обе части неравенства отрицательные. Умножим обе части неравенства на отрицательное число 
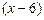, получим
.
2) Если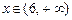 
, то обе части неравенства положительные. Умножим обе части неравенства на положительное число 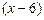, получим
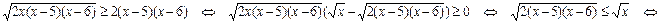
Иррациональные неравенства, содержащие знак модуля
Пример 34. Решите неравенство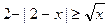 
. Ответ: 
.
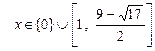Решение.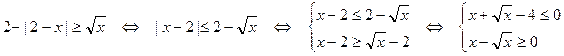 
Решим неравенства заменой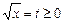 
.
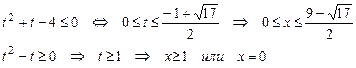. Общее решение:
Пример 35. Решить неравенство 
Ответ: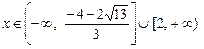 
Решение.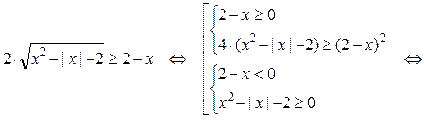 
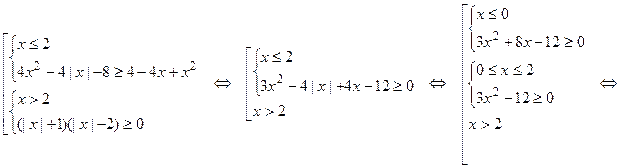
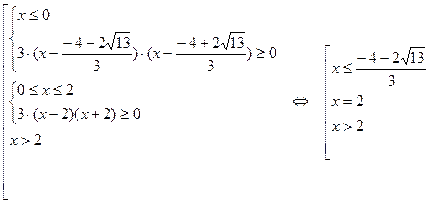
Системы иррациональных уравнений и неравенств
И методы их решения
Методы решения систем иррациональных уравнений и неравенств, сводятся к методам решения иррациональных уравнений и неравенств, входящих в систему.
Пример 36. Решите систему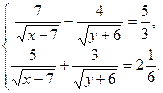 
Решение: Область допустимых значений неизвестных:
Положим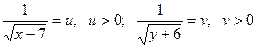 
, тогда получим систему уравнений:
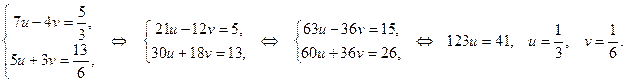
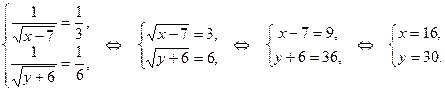
Ответ: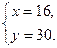 
Пример 37. Решите систему уравнений 
Решение: Положим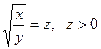 
, тогда 
, второе уравнение примет вид:
Таким образом, получим: 
Подставляя в первое уравнение, найдем значение :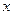 
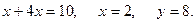
Подставим второе значение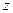 
и найдем 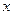и 
:
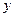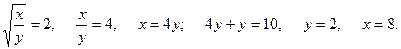
Ответ: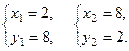 
Пример 38. Решите систему 
Решение: Область допустимых значений определяется совокупностью двух систем неравенств: 
Преобразуем первое уравнение системы:
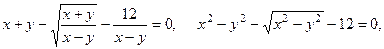поскольку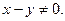 
Положим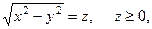 
получим квадратное уравнение:
Поскольку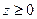 
, то первый корень является посторонним, остается один корень 
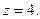Систем уравнений примет вид: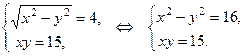 
Умножим первое уравнение на 15, а второе на -16 и сложим левые и правые части этих уравнений, придем к однородному уравнению.
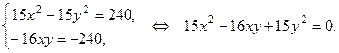
Заметим, что 
и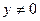 
, в противном случае, второе уравнение 
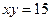обращается в ложное равенство: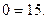 
Разделим обе части уравнения на 
, получим уравнение: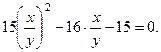 
Положим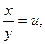 
тогда получим квадратное уравнение:
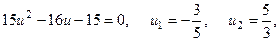тогда 
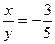и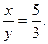 
Получим две системы уравнений: (1)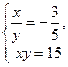 
и (2)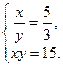 
Решим первую систему: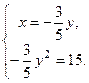 
Эта система решений не имеет.
Решим вторую систему: 
Обе пары значений входят в область допустимых значений.
Ответ: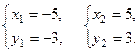 
Домашнее задание № 1
Класс
1. Решить уравнение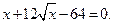 
2. Решить уравнение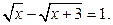 
3. Решить уравнение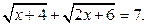 
4. Решить уравнение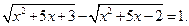 
5. Решить уравнение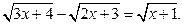 
6. Чему равна сумма целочисленных решений неравенства 
?
7. Решить неравенство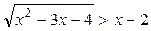 
.
8. Решить неравенство 
.
9. Решить неравенство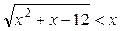 
.
10. Решить неравенство 
.
11. Решите неравенство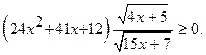 
12. Решить неравенство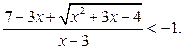 
13. Решить неравенство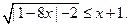 
14. Решите систему уравнений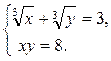 
15. Решите неравенство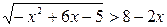 
.
16. Решите неравенство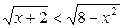 
.
17. Решить неравенство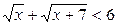 
.
18. Найти максимальное и минимальное значение функции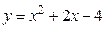 
на множестве решений неравенства 
.
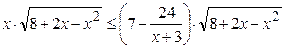19. Решить неравенство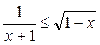 
20. Найдите наименьший из корней уравнения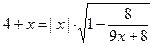 
Желаем успехов!
Дата добавления: 2019-01-14; просмотров: 257; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!