Использование монотонности функции.
ФГБОУ ВО «ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Заочная физико-математическая школа
МАТЕМАТИКА
ЗАДАНИЕ № 1
Класс
Иррациональные уравнения и неравенства
Мы предполагаем, что учащиеся ЗФМШ имеют определённые навыки тождественных преобразований уравнений и неравенств, раскрытия модулей, выполнения замены переменной и т.п. А приведённые ниже краткие решения стандартных заданий помогут учащимся успешно выполнить домашнее задание.
Уравнения, в которых неизвестная величина находится под знаком радикала называются иррациональными.
К простейшим иррациональным уравнениям относятся уравнения вида:
.
Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. При решении иррациональных уравнений речь всегда идет об отыскании действительных корней. Область допустимых значений иррационального уравнения состоит из тех значений неизвестных, при которых неотрицательными являются все выражения, стоящие под знаком радикала четной степени.
Иррациональные уравнения решаются, в основном возведением обеих частей уравнения в натуральную степень, то есть переходом от уравнения
(1)
к уравнению
|
|
|
. (2)
Справедливы следующие утверждения:
1) при любом 
уравнение (2) является следствием уравнения (1);
2) если 
(n – нечетное число), то уравнения (1) и (2) равносильны;
3) если 
(n – четное число), то уравнение (2) равносильно уравнению
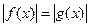, (3)
а уравнение (3) равносильно совокупности уравнений
. (4)
В частности, уравнение
(5)
равносильно совокупности уравнений (4).
Пример 1. Решить уравнение 
.
Решение. Запомните, что возводить в квадрат можно обе части уравнения, только если они обе неотрицательны, т.е. наше уравнение равносильно системе
откуда следует что 
, а корень 
не удовлетворяет второму неравенству. При этом грамотное решение не требует проверки.
Ответ: .
Пример 2. Решить уравнение 
.
Решение. Это уравнение равносильно системе
Решая первое уравнение этой системы, равносильное уравнению 
, получим корни 
и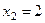 
. Однако при этих значениях x не выполняется неравенство 
, и потому данное уравнение не имеет корней.
Ответ: корней нет.
Пример 3. Решить уравнение
|
|
|
.
Решение. Уединив первый радикал, получаем уравнение
,
равносильное исходному.
Возводя обе части этого уравнения в квадрат, так как они обе положительны, получаем уравнение
,
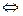
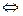
которое является следствием исходного уравнения. Возводя обе части этого уравнения в квадрат при условии, что 
, приходим к уравнению
.
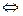
Это уравнение имеет корни 
, 
. Первый корень удовлетворяет исходному условию 
, а второй – не удовлетворяет.
Ответ: 
.
Удобным средством решения иррациональных уравнений иногда является метод введения новой переменной, или «метод замены». Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную.
Пример 4. Решите уравнение 
.
Решение: Сделаем замены: 
, 
. Исходное уравнение перепишется в виде 
, откуда находим, что а = 4b и 
(тогда 
) . Далее, возводя обе части уравнения 
в квадрат, получаем: 
. Отсюда х = 15 .
Ответ: 15..
Пример 5. Решить уравнение
.
Решение:Положив 
, получим существенно более простое иррациональное уравнение 
. Возведем обе части уравнения в квадрат: 
.
|
|
|
Далее последовательно получаем:
; 
;
; 
; 
, 
.
Проверка найденных значений их подстановка в уравнение 
показывает, что 
– корень уравнения, а – посторонний корень.
Возвращаясь к исходной переменной x, получаем уравнение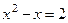 
, то есть квадратное уравнение 
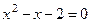, решив которое находим два корня: , 
. Оба корня удовлетворяют исходному уравнению.
Ответ: , .
Замена особенно полезна, если в результате достигается новое качество, например, иррациональное уравнение превращается в рациональное.
Пример 6. Решить уравнение 
.
Решение: Перепишем уравнение так: 
.
Видно, что если ввести новую переменную 
, то уравнение примет вид 
, откуда 
- посторонний корень и 
.
Из уравнения 
получаем 
, 
.
Ответ: , 
.
Пример 7. Решить уравнение 
.
Решение: Введем новую переменную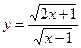 
, 
.
В результате исходное иррациональное уравнение принимает вид квадратного 
, откуда, учитывая ограничение 
, получаем 
. Решая уравнение 
, получаем корень 
.
Ответ: 2,5.
Иногда иррациональное уравнение удается решить довольно быстро, если обе его части умножить на удачно подобранную функцию. Конечно, при умножении обеих частей уравнения на некоторую функцию могут появиться посторонние решения, ими могут оказаться нули самой этой функции. Поэтому предлагаемый метод требует обязательной проверки получающихся значений.
|
|
|
Пример 8. Решить уравнение 
.
Решение: ОДЗ: 
. Умножим обе части уравнения на одну и ту же функцию 
, отметим, что в ОДЗ она положительна. Выражение 
называется сопряженным для выражения 
. Цель такого умножения ясна: использовать тот факт, что произведение двух сопряженных выражений уже не содержит радикалов.
В результате этого умножения и очевидных преобразований приходим к уравнению 
которое равносильно совокупности уравнений 
Возводя в квадрат второе уравнение совокупности, и, с учетом ОДЗ, получим
.
Если внимательно посмотреть на неравенства последней системы, можно заметить, что пересечение множеств 
и 
пусто. Следовательно, уравнение 
решений не имеет. Значит, исходное уравнение имеет единственный корень 
.
Подстановка в исходное уравнение показывает, что – корень.
Ответ: 0.
Пример 9. Решите уравнение 
.
Решение: Умножив обе части уравнения на сопряженную левой части функцию: 
, получим
.
Приведем подобные слагаемые и получим равносильное уравнение
.
Сложив исходное уравнение и последнее, получим
Ответ: 
.
Некоторые иррациональные уравнения приводятся к рациональным, если увидеть полный квадрат в подкоренных выражениях.
Пример 10. Решите уравнение 
.
Решение: Произведем замену переменной 
.
Подставим замену в исходное уравнение
.
Последнее уравнение равносильно уравнению вида 
. Определим интервалы знакопостоянства выражений, стоящих под знаком модуля.
Составим совокупность, раскрывая модуль в каждом из указанных промежутков.
Вернемся к замене переменной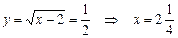 
.
Ответ: 
.
Пример 11. Решите уравнение 
Решение: Область допустимых значений: 
или 
Преобразуем уравнение так, чтобы получить сумму двух полных квадратов:
Сумма двух неотрицательных выражений равна нулю тогда и только тогда, когда оба выражения равны нулю!
Поэтому наше равенство будет выполняться тогда и только тогда, когда 
что получается только при одном значении 
, 
Ответ: 
Использование монотонности функции.
Пусть уравнение имеет вид: 
где 
возрастает (убывает), или 
где 
и 
«встречно монотонны», т.е. возрастает, а убывает или наоборот, то такое уравнение имеет не более одного корня. Если удается заметить это или привести уравнение к такому виду и при этом нетрудно угадать корень, то он и будет единственным решением данного уравнения.
Пример 12. Решите уравнение 
.
Решение: Это уравнение можно попытаться решить возведением в квадрат (трижды!). Однако при этом получится уравнение четвертой степени. Попробуем угадать корень. Это сделать нетрудно: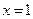 
. Теперь заметим, что левая часть уравнения – возрастающая функция, а правая – убывающая. Но это значит, что больше одного корня такое уравнение иметь не может. Итак, 
– единственный корень.
Ответ: 
.
Пример 13. Решить уравнение 
.
Решение: Как и в предыдущих примерах, несложно обнаружить, что 
– корень. ОДЗ
исходного уравнения – промежуток 
. Но теперь уже, в отличие от ранее рассмотренных задач, левая часть уравнения не задает монотонную функцию. Однако снова легко заметить, что на 
указанная функция возрастает, причем корень 
принадлежит этому промежутку. Значит, на 
данное уравнение имеет единственный корень. Осталось исследовать поведение функции 
на отрезке 
. Очевидно, что при 
, а 
, поэтому 
Следовательно, при 
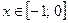исходное уравнение корней не имеет.
Ответ: 
.
Использование ОДЗ
Иногда знание ОДЗ позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из ОДЗ.
Пример 14. Решить уравнение 
.
Решение: Конечно, это иррациональное уравнение можно решить путем традиционного возведения обеих частей в квадрат. Однако, найдя ОДЗ этого уравнения, приходим к выводу, что ОДЗ исходного уравнения – одноэлементное множество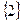 
. Подставив в данное уравнение, приходим к выводу, что – корень исходного уравнения.
Ответ: 
.
Дата добавления: 2019-01-14; просмотров: 887; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!