Иррациональные уравнения, содержащие знак модуля
Простейшие уравнения с модулем имеют вид:  и
и  ; будем их решать на основании определения модуля сведением к совокупности систем.
; будем их решать на основании определения модуля сведением к совокупности систем.
Пример 19. Решить уравнение  .
.
Решение: Уравнение имеет решение только при условии, что правая часть уравнения неотрицательна, т.е. 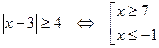 . Однако, при
. Однако, при  подкоренное выражение отрицательно. Таким образом,
подкоренное выражение отрицательно. Таким образом,  , т.е. модуль раскрывается однозначно «с плюсом». Получаем равносильное уравнение
, т.е. модуль раскрывается однозначно «с плюсом». Получаем равносильное уравнение  . Возводя в квадрат, получим уравнение
. Возводя в квадрат, получим уравнение  , корни которого
, корни которого  . Второй корень – посторонний.
. Второй корень – посторонний.
Ответ: 
Пример 20. Решить уравнение  .
.
Решение: Так как левая часть уравнения при всех допустимых значениях аргумента неотрицательна, то и правая должна быть неотрицательной, т.е.  . Тогда модуль раскрывается однозначно:
. Тогда модуль раскрывается однозначно:  . Получаем уравнение
. Получаем уравнение  . Возводя в квадрат, получаем равносильное уравнение
. Возводя в квадрат, получаем равносильное уравнение  как в примере 19 с тем же условием на аргумент. Поэтому
как в примере 19 с тем же условием на аргумент. Поэтому
Ответ: 
Пример 21. Решить уравнение  .
.
Решение: Важно помнить, что  , а равенство
, а равенство  верно, только если Вы точно знаете, что
верно, только если Вы точно знаете, что  .
.
Уравнение теперь легко решается 
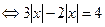
 .
.
Ответ:  .
.
Методы решения иррациональных неравенств
Иррациональные неравенства – довольно сложный раздел школьного курса математики, и на его изучение отведено крайне мало времени. Решение иррациональных неравенств осложняется тем обстоятельством, что здесь, как правило, исключена возможность проверки, поэтому надо стараться делать все преобразования равносильными.
|
|
|
Чтобы избежать ошибок при решении иррациональных неравенств, следует рассматривать только те значения переменной, при которых все входящие в неравенство функции определены, то есть найти ОДЗ этого неравенства, а затем обоснованно осуществлять равносильный переход на всей ОДЗ или ее частях.
При решении иррациональных неравенств следует запомнить правило: при возведении обеих частей неравенства в нечетную степень всегда получается неравенство, равносильное данному неравенству.
Если обе части неравенства возводят в четную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны.
Основным методом решения иррациональных неравенств является сведение исходного неравенства к равносильной системе или совокупности систем рациональных неравенств.
Иррациональное неравенство 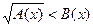 или
или 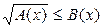 равносильно системе неравенств
равносильно системе неравенств
 или
или  . (1)
. (1)
Иррациональное неравенство  или
или  равносильно совокупности двух систем неравенств
равносильно совокупности двух систем неравенств

 или
или 
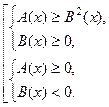 . (2)
. (2)
Иррациональное неравенство  или
или  равносильно системе неравенств
равносильно системе неравенств
|
|
|
 или
или  . (3)
. (3)
Пример 22. Решить неравенство  .
.
Решение: Как и в предыдущем примере, заметим, что правая часть данного неравенства отрицательна, а левая часть исходного неравенства неотрицательна при всех значениях x, при которых она определена. Это означает, что левая часть больше правой части при всех значениях x, удовлетворяющих условию  .
.
Ответ:  .
.
Пример 23. Решить неравенство  .
.
Решение: Это неравенство может быть решено при помощи схемы (1). Система, равносильная исходному неравенству, имеет вид



 .
.
Ответ:  .
.
Пример 24. Решить неравенство  .
.
Решение: Данное неравенство можно решать с помощью схемы (2).
Обратите внимание, что при отрицательной правой части неравенство «в сторону больше» всегда верно в ОДЗ.
Неравенство равносильно совокупности двух систем



Ответ:  .
.
Пример 25. Решить неравенство 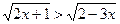 .
.
Решение:Согласно схеме (3), данное неравенство равносильно системе
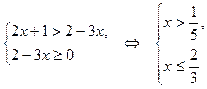

Ответ: 
Пример 26. Решить неравенство  .
.
Решение: Перенесем второй радикал в правую часть, чтобы обе части неравенства стали неотрицательными, и его можно было возвести в квадрат:

Мы пришли к простейшему стандартному неравенству, которое согласно схеме (1) равносильно системе:
|
|
|

Ответ:  .
.
Замечание. При получении неравенства  не выписывали допустимые значения неизвестного, так как там фигурировал
не выписывали допустимые значения неизвестного, так как там фигурировал  , который существует при
, который существует при  , но при этих значениях
, но при этих значениях  существует и
существует и  .
.
Пример 27. Решить неравенство  .
.
Решение: Начнем с отыскания допустимых значений неизвестного:

Заметим, что для избавления от радикала достаточно возвести данное неравенство в квадрат. Но для этого необходимо, чтобы обе части его были неотрицательны, что выполняется лишь при выполнении условия  (так как все остальные выражения, входящие в неравенство, неотрицательны). Но при этом условии можно умножить данное неравенство на положительное выражение
(так как все остальные выражения, входящие в неравенство, неотрицательны). Но при этом условии можно умножить данное неравенство на положительное выражение  .
.
Итак, если  , данное неравенство преобразуется и решается так:
, данное неравенство преобразуется и решается так:

В том случае, когда  , данное неравенство будет выполняться, так как его отрицательная левая часть станет меньше положительной правой и все такие x входят в ОДЗ.
, данное неравенство будет выполняться, так как его отрицательная левая часть станет меньше положительной правой и все такие x входят в ОДЗ.
Ответ: 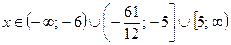 .
.
Пример 28. Решить неравенство  .
.
Решение: Найдем ОДЗ: 
Умножим обе части данного неравенства на выражение, сопряженное его левой части и, очевидно, положительное в ОДЗ:
 .
.
Дальнейшее решение зависит, очевидно, от знака множителя  .
.
Если он меньше нуля, то есть  , сократив на этот отрицательный множитель (при этом меняется знак неравенства), переходим к неравенству:
, сократив на этот отрицательный множитель (при этом меняется знак неравенства), переходим к неравенству:  , из которого получаем прямым возведением в квадрат (ведь обе части этого неравенства положительны)
, из которого получаем прямым возведением в квадрат (ведь обе части этого неравенства положительны) 
|
|
|


Отсюда с учетом ОДЗ и убедившись, что  , находим:
, находим: 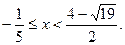
Во втором случае, если множитель положителен (то есть при  ), после сокращения на него получаем неравенство
), после сокращения на него получаем неравенство  , которое очевидно выполняется при
, которое очевидно выполняется при 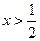 , так как
, так как 
Осталось указать, что в третьем возможном случае – если общий множитель равен нулю, – неравенство не выполняется: мы получаем тогда  , что неверно.
, что неверно.
Ответ:  .
.
Иногда удается иррациональную функцию, входящую в неравенство, заменить новой переменной таким образом, что относительно этой переменной неравенство становится рациональным.
Пример 29. Решить неравенство  .
.
Решение: Введем новую переменную  ,
,  .
.
Тогда 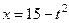 и для переменной t получаем рациональное неравенство
и для переменной t получаем рациональное неравенство


 .
.
Осталось сделать обратную замену и найти 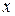 :
:

Ответ:  .
.
Дата добавления: 2019-01-14; просмотров: 2900; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
