Глава 4. РАВНОВЕСНОЕ ДВИЖЕНИЕ РАКЕТЫ ПРИ КОМПЕНСИРОВАНИИ ВНЕШНЕГО СОПРОТИВЛЕНИЯ РЕАКТИВНОЙ ТЯГОЙ
Основное дифференциальное уравнение с эффективной массой
В случае пренебрежения силами гравитации уравнение одномерного движения ракеты в рамках специальной теории относительности имеет вид
, 
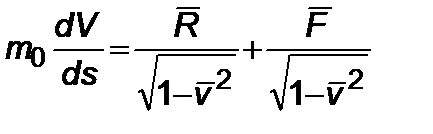, (4.1.1)
где нормированные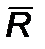 
– реактивная тяга, 
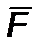– сила сопротивления внешней разреженной среды; их можно представить в виде 
, 
, 
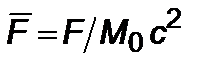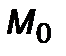– начальная масса; здесь
, 
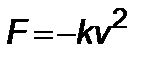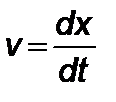, (4.1.2)
в случае ньютоновской механики, и
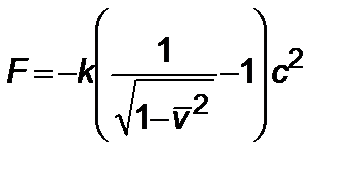, (4.1.3)
в случае релятивистской механики (при 
имеем (4.1.2)). Коэффициент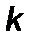 
для движения тел в сопротивляющейся среде обычно принимается в виде
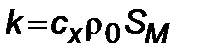, (4.1.4)
где 
– коэффициент сопротивления,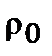 
– плотность среды, 
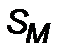– площадь миделя условной ракеты. Коэффициент для движения тел с первой космической скоростью в верхних слоях атмосферы рассчитывается методом Монте-Карло ( 
) и, очевидно, не будет соответствовать условиям полета при миллисветовых скоростях, когда взаимодействие частиц внешней среды с оболочкой ракеты будет носить более жесткий, неупругий характер, и будет изменяться величина условной площади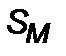 
. Поскольку отсутствуют экспериментальные данные для расчета 
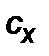, предположим для простоты постоянство коэффициента
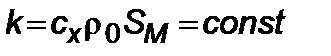, где 
, 
.
Тогда из (4.1) имеем
|
|
|
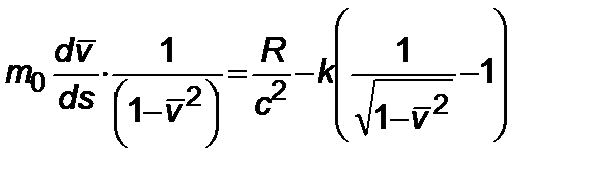. (4.1.5)
Можно полагать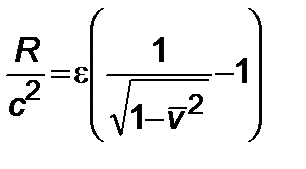 
, где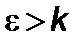 
.
Условие, когда внешнее сопротивление компенсируется реактивной тягой, есть 
и
, (4.1.6)
где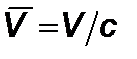 
– предельная скорость, отсюда величина 
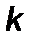определяется в виде
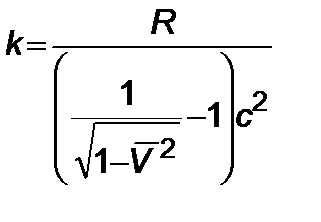. (4.1.7)
Таким образом, исключается коэффициент 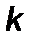. Подставляя (4.1.7) в (4.1.5), получим
, 
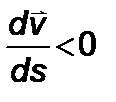, (4.1.8)
где эффективная масса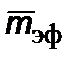 
есть
. (4.1.9)
В общем случае 
; 
, 
.
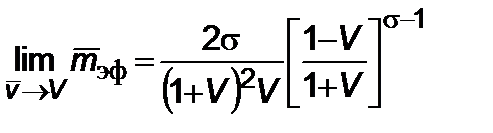Закон изменения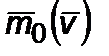 
в общем случае зависит от скорости истечения 
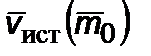, безразмерного параметра 
, зависящего от внешнего заряда (если продукты выхлопа заряженные); обозначим выражение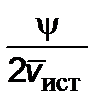 
через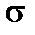 
, 
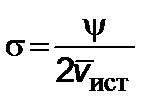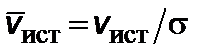. (4.1.10)
Для простоты воспользуемся законом изменения 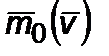при постоянном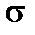
. (4.1.11)
Для произвольного значения 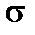удобно аппроксимировать (4.1.11) двумя линейными функциями. Этот подход облегчает решение (4.1.8). Для этого возьмем производную 
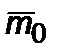по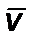 
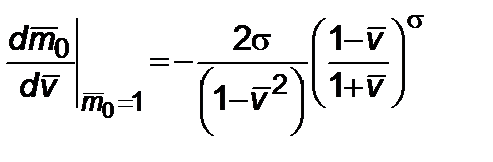. (4.12)
При 
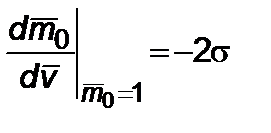; представим 
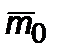в виде 
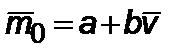. Построим график 
.
|
|
|
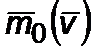Рис.3. Аппроксимация функции 
Из графика на рис.3 определим
, 
,
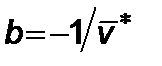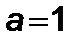где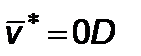 
– значение скорости сосредоточенной массы в точке 
пересечения касательно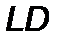й 
оси 
. Из геометрических соображений имеем
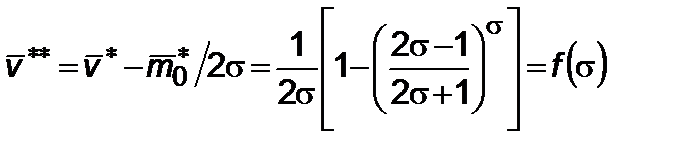. (4.1.13)
Итак, аппроксимацию произведем двумя функциями: на первом участке от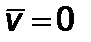 
до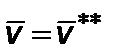 
, а на втором – от 
до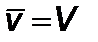 
; 
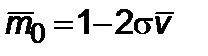– первый участок и 
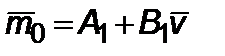– второй участок, где
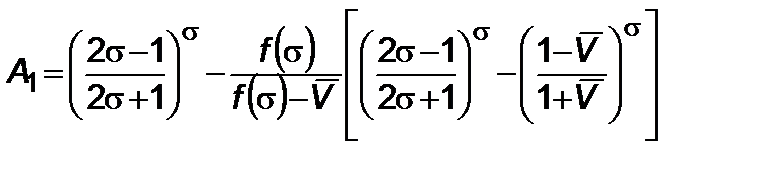, (4.1.14)
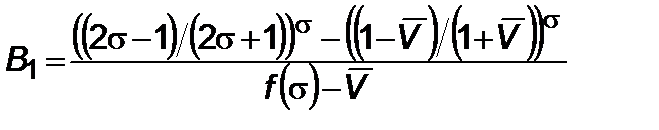. (4.1.15)
Погрешность, возникающая за счет аппроксимации, равна по ординате
, (4.1.16)
и по абсциссе
. (4.1.17)
Кинематика движения
Итак, для первого участка
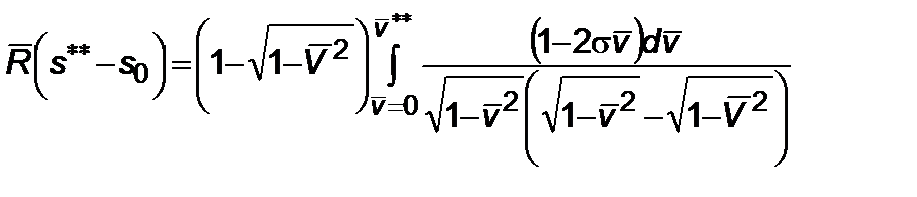, (4.2.1)
для второго участка 
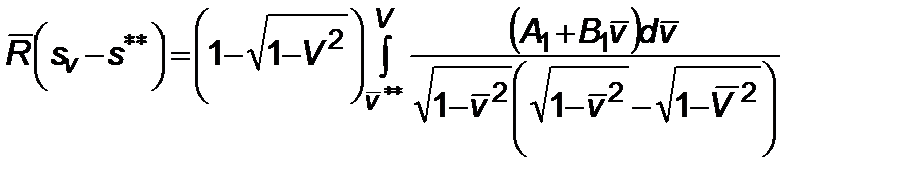. (4.2.2)
Таким образом, определяется кинематика переходного участка при 
.
Для (4.2.1) интегрирование дает
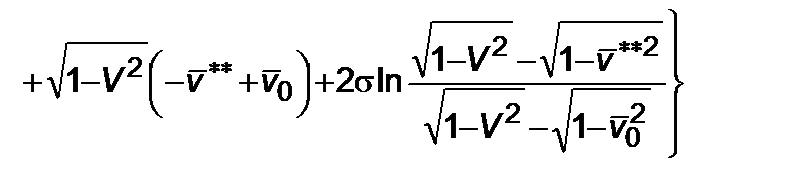. (4.2.3)
Для (4.2.2) интегрирование дает
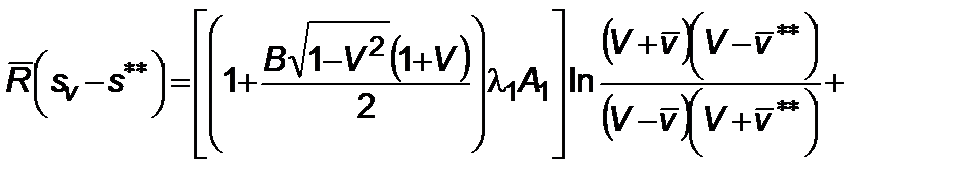
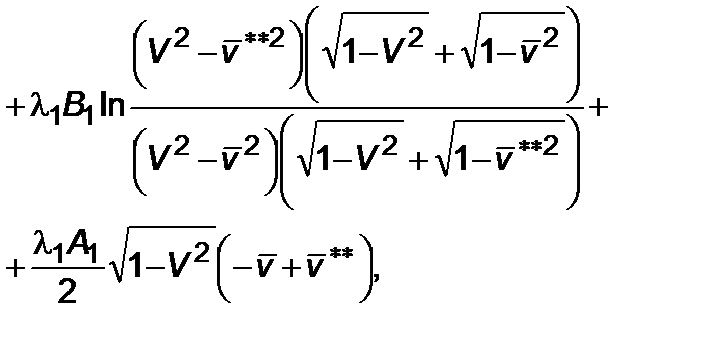(4.2.4)
.
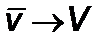Глава 5. ДВИЖЕНИЕ РАКЕТЫ В СИЛЬНОМ ГРАВИТАЦИОННОМ ПОЛЕ
Особенности движения в поле Шварцшильда
При движении релятивистской ракеты возможна встреча с коллапсированной звездой (“черной дырой” или “коллапсаром”). Моделируя “черную дыру” метрикой Шварцшильда, можно классифицировать орбиты ракеты; интенсивность поля гравитации столь высока, что небесное тело (ракета) при близком прохождении может быть втянуто внутрь “дыры”. Итак, рассмотрим метрику Шварцшильда
|
|
|
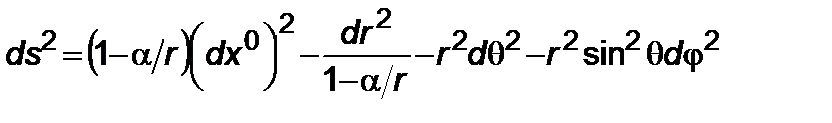. (5.1.1)
Здесь 
, 
, 
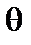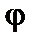– координаты кривизны, 
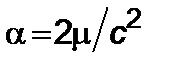– гравитационный радиус, 
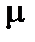– гравитационная постоянная. Интегралы энергии 
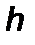и моменты количества движения при 
есть
, 
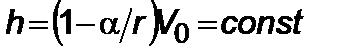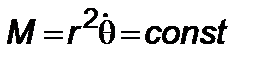. (5.1.2)
Из (2.3.4) при действии реактивного ускорения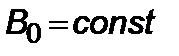 
следует первый интеграл
. (5.1.3)
Комбинируя (5.1.3) с интегралом, следующим из (5.1.1) и (5.1.2)
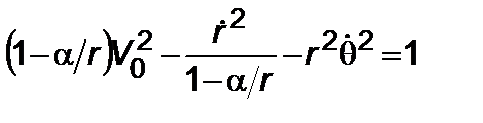, (5.1.4)
,
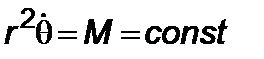получим основное уравнение траектории
, 
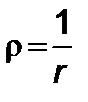, (5.1.5)
где
. (5.1.6)
Выражение (5.1.6) – алгебраическое уравнение пятой степени, в отличие от третьей степени для случая отсутствия реактивного ускорения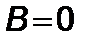 
. Упрощая (5.1.6) для случая 
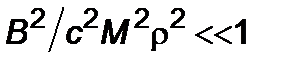, приходим к уравнению четвертой степени, имеющему четыре корня 
, 
, 
, 
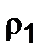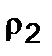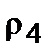; можно далее получать в соответствии с методом Чандрасекхара [8], классы орбит с эксцентриситетом 
, 
, 
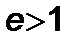, многие из которых отсутствуют в ньютоновской небесной механике. В частности, для можно 
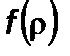представить в виде
|
|
|
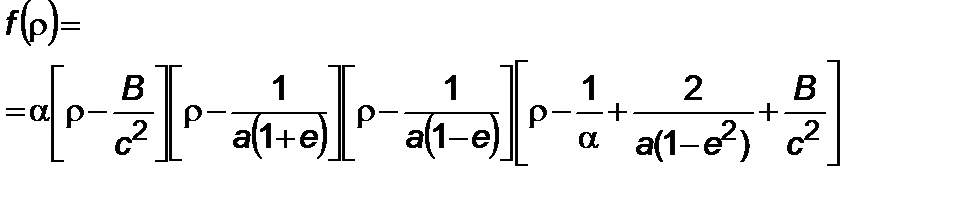(5.1.7)
и получить связь между 
, 
, 
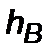и 
, 
, где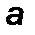 
– полуось орбиты. Оценки показали, что вблизи “черной дыры” эффект от возмущения реактивной тяги весьма мал и не влияет на гравитационную эволюцию ракеты даже при реактивной перегрузке 
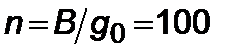. Поэтому следует выделить при движении ракеты в сильном гравитационном поле три зоны – первая, описанная выше, где ракета становится неуправляемой, вторая зона, когда возмущения от сил гравитации и сил реактивных примерно равны, и третья зона, когда реактивное ускорение превосходит силу тяготения “черной дыры”.
Дата добавления: 2019-01-14; просмотров: 177; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!