Уравнения релятивистской баллистики
Если спроектировать в евклидовой плоскости уравнения движения (2.2.7) и энергии ракеты (2.2.8), то получим
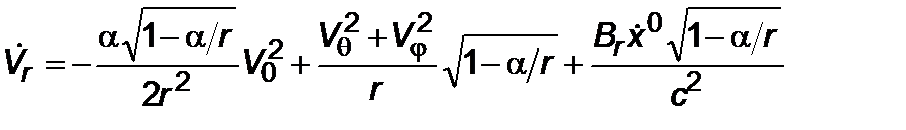 , (2.3.1)
, (2.3.1)
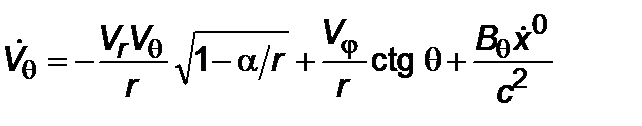 , (2.3.2)
, (2.3.2)
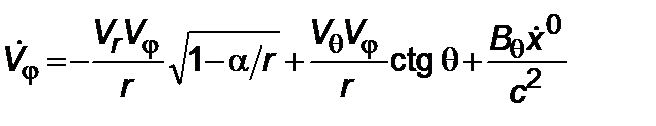 , (2.3.3)
, (2.3.3)
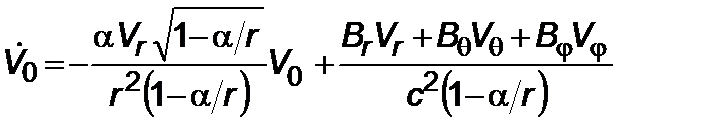 . (2.3.4)
. (2.3.4)
Здесь 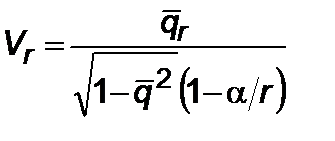 ,
, 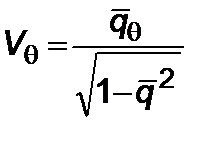 ,
, 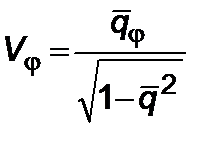 .
.
Проекции записаны вдоль координат кривизн 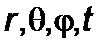 . Для плоского движения, учитывая соотношения
. Для плоского движения, учитывая соотношения
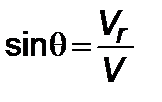 ,
, 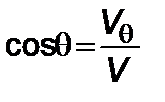 , (2.3.5)
, (2.3.5)
где 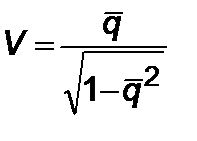 , имеем
, имеем
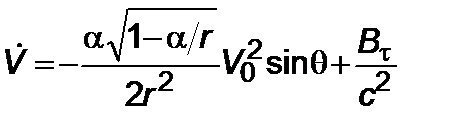 , (2.3.6)
, (2.3.6)
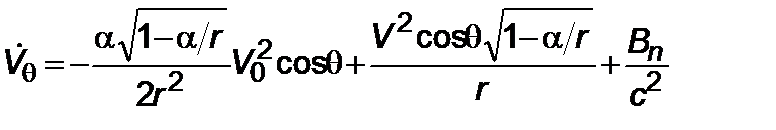 , (2.3.7)
, (2.3.7)
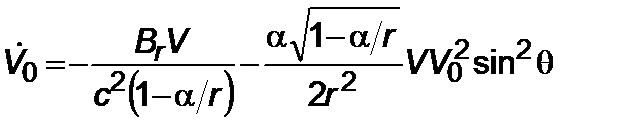 , (2.3.8)
, (2.3.8)
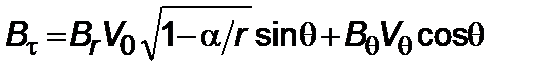 , (2.3.9)
, (2.3.9)
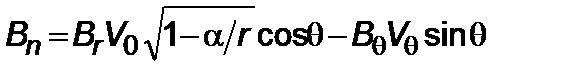 (2.3.10)
(2.3.10)
или
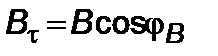 ,
,  , (2.3.11)
, (2.3.11)
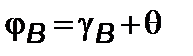 ,
, 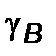 – угол между касательной к траектории и модулем реактивного ускорения. Наконец
– угол между касательной к траектории и модулем реактивного ускорения. Наконец
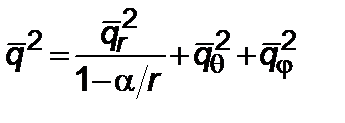 . (2.3.12)
. (2.3.12)
Таким образом, дана полная система уравнений релятивистской баллистики ракеты. В пределе малых скоростей и слабых полей они сводятся к классическим уравнениям баллистики космических ракет в ньютоновском поле.
Кинематика движения с постоянным реактивным ускорением
Рассмотрим одномерное движение ракеты при пренебрежении гравитационным полем 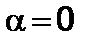 . Тогда получим
. Тогда получим
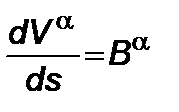 ,
, 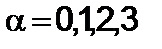 , (2.4.1)
, (2.4.1)
где 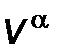 ,
, 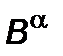 – компоненты 4-х скоростей и 4-х ускорений при
– компоненты 4-х скоростей и 4-х ускорений при 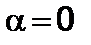 . Положим, что модуль реактивного ускорения
. Положим, что модуль реактивного ускорения 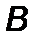 постоянен,
постоянен, 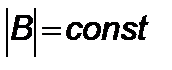 . Это означает, что скалярный квадрат
. Это означает, что скалярный квадрат 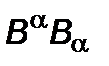 должен сохранять свое значение в произвольной системе отсчета
должен сохранять свое значение в произвольной системе отсчета
|
|
|
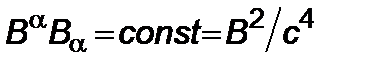 . (2.4.2)
. (2.4.2)
В случае сигнатуры (–+++) по определению
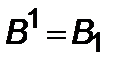 ,
, 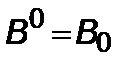
( 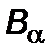 – ковариантное,
– ковариантное, 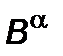 – контравариантное значение). Тогда
– контравариантное значение). Тогда
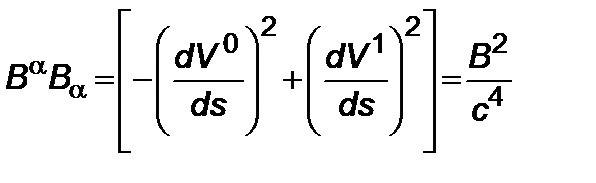 . (2.4.3)
. (2.4.3)
С учетом (2.4.2), после интегрирования (2.4.3) имеем
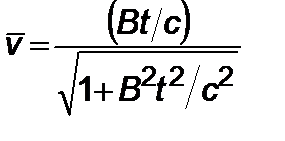 ,
, 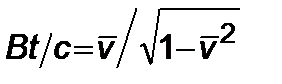 , (2.4.4)
, (2.4.4)
но 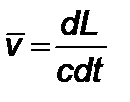 , где
, где 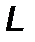 – пройденный ракетой путь. Интегрирование (2.4.4) дает
– пройденный ракетой путь. Интегрирование (2.4.4) дает
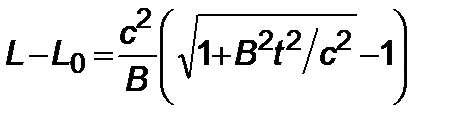 . (2.4.5)
. (2.4.5)
Интегрируя теперь выражение (1) 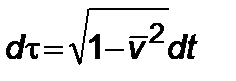 , получим зависимость между собственным временем
, получим зависимость между собственным временем 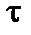 в ракете и временем внешнего наблюдателя (на Земле)
в ракете и временем внешнего наблюдателя (на Земле)
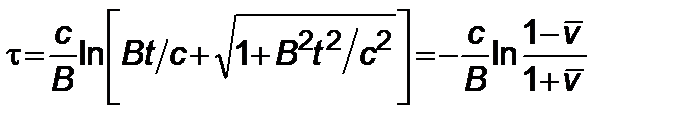 . (2.4.6)
. (2.4.6)
Выражая 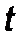 из
из 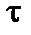 и подставляя в (2.3.5), имеем
и подставляя в (2.3.5), имеем
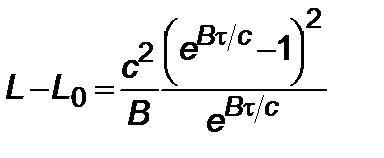 . (2.4.7)
. (2.4.7)
Возьмем производную 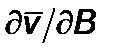 , используя (2.4.)
, используя (2.4.)
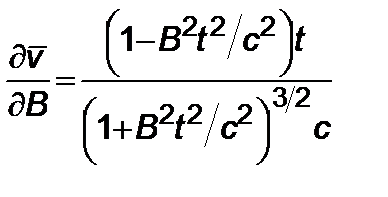 , (2.4.8)
, (2.4.8)
тогда 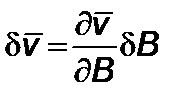 ;
;
производную из (2.4.5) 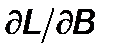 , используя (2.4.5)
, используя (2.4.5)
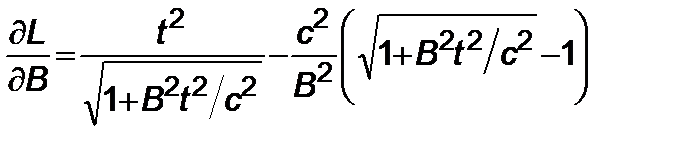 , (2.4.9)
, (2.4.9)
тогда 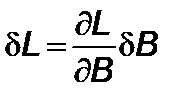 .
.
Таким образом, определяется кинематика. Поскольку по определению 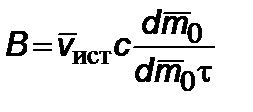 , то можно определить расход массы в зависимости от бортового времени
, то можно определить расход массы в зависимости от бортового времени
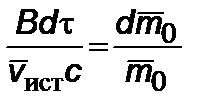 ,
, 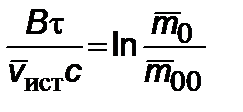 ,
, 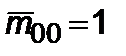 ,
, 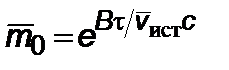 . (2.4.10)
. (2.4.10)
Кинематика движения с постоянной реактивной тягой
Рассмотрим вновь одномерное движение ракеты при постоянной тяге  . Исходя по аналогиииз выражения (2.4.3), получим уравнение
. Исходя по аналогиииз выражения (2.4.3), получим уравнение
|
|
|
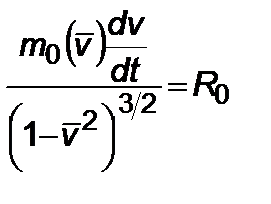 . (2.5.1)
. (2.5.1)
Но, согласно определению, выражение для тяги есть
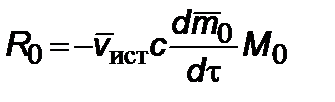 , (2.5.2)
, (2.5.2)
где 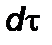 – элемент собственного времени. Интегрируя (2.5.2), получим
– элемент собственного времени. Интегрируя (2.5.2), получим
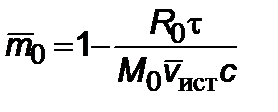 . (2.5.3)
. (2.5.3)
Подставляя (2.5.3) в (2.5.1), имеем 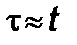
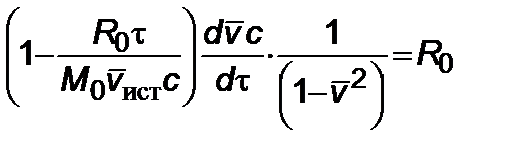 ,
,
или
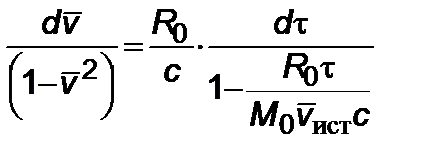 . (2.5.4)
. (2.5.4)
Интегрируя (2.5.4), получим зависимость скорости 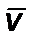 от времени
от времени 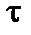
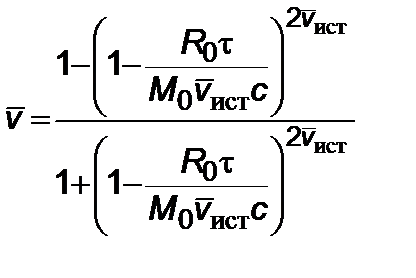 . (2.5.5)
. (2.5.5)
Обозначим через 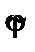 выражение, где вновь положим
выражение, где вновь положим 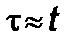
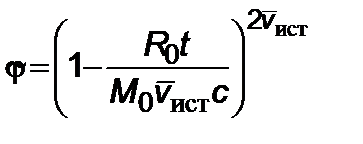 ,
, 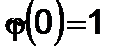 , (2.5.6)
, (2.5.6)
тогда
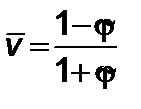 . (2.5.7)
. (2.5.7)
Разложим скорость 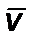 в ряд Тейлора
в ряд Тейлора
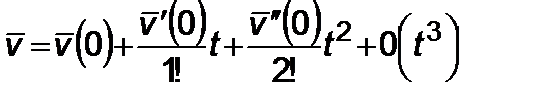 . (2.5.8)
. (2.5.8)
Тогда
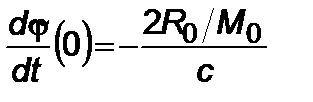 ,
, 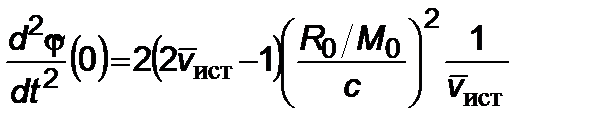 . (2.5.9)
. (2.5.9)
Из (2.5.7) следует
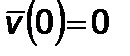 ,
, 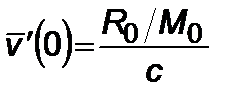 ,
, 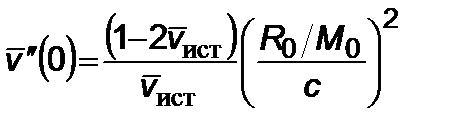 . (2.5.10)
. (2.5.10)
Итак,
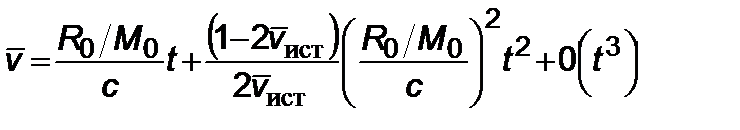 . (2.5.11)
. (2.5.11)
Но 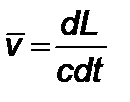 , тогда дальность получим из (2.5.11)
, тогда дальность получим из (2.5.11)
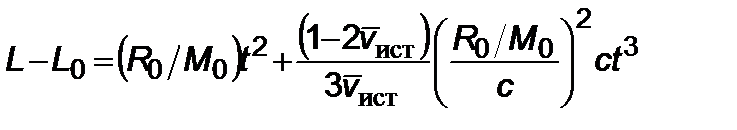 . (2.5.12)
. (2.5.12)
Для данного отрезка времени 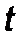 поправка для дальности есть
поправка для дальности есть
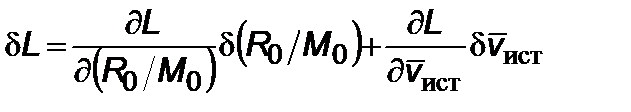 , (2.5.13)
, (2.5.13)
где
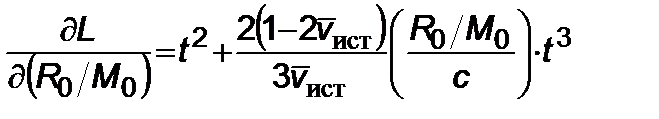 (2.5.14)
(2.5.14)
и
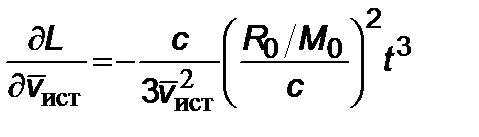 . (2.5.15)
. (2.5.15)
Запишем теперь условие достижения заданного ускорения (перегрузки 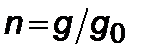 ) при движении с постоянной тягой
) при движении с постоянной тягой
|
|
|
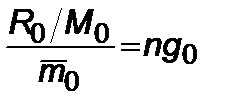 , (2.5.16)
, (2.5.16)
где  .
.
Условие для времени есть
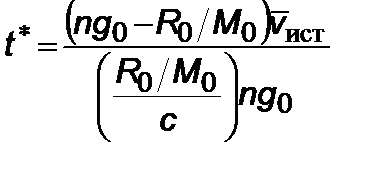 . (2.5.17)
. (2.5.17)
Соответствующее расстояние есть
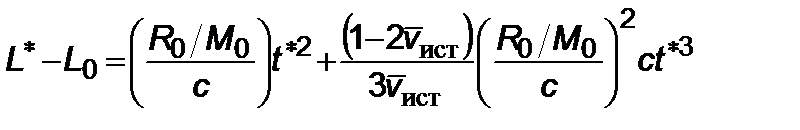 . (2.5.18)
. (2.5.18)
Кинематика движения с постоянной мощностью
Если спроектировать (2.2.4) при 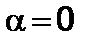 на времениподобное направление
на времениподобное направление 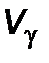 , то получим выражение для изменения мощности
, то получим выражение для изменения мощности
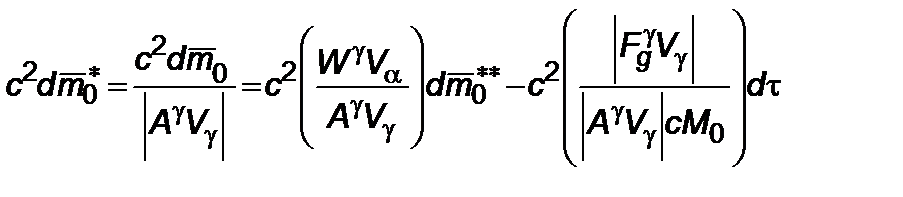 . (2.6.1)
. (2.6.1)
Инварианты 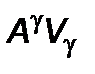 ,
, 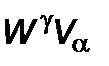 ,
, 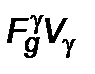 определяются на основе лоренцова сложения скоростей. Инвариант
определяются на основе лоренцова сложения скоростей. Инвариант 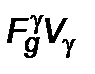 определяет изменение тепловой энергии
определяет изменение тепловой энергии  за счет диссипативных процессов. Записывая теперь выражение дефекта массы покоя
за счет диссипативных процессов. Записывая теперь выражение дефекта массы покоя 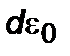
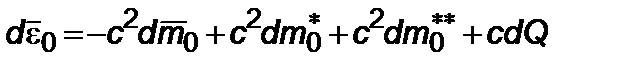 , (2.6.2)
, (2.6.2)
прибавляя к (2.6.2) выражение (2.6.1), имеем выражение для мощности в безразмерной форме
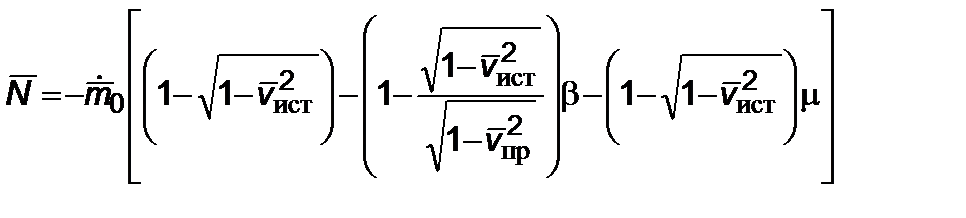 . (2.6.3)
. (2.6.3)
Здесь 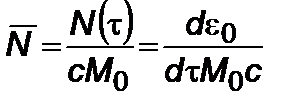 ,
, 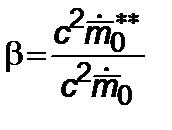 ,
, 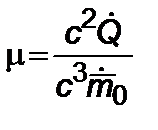 ,
, 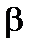 – доля вносимой в ракету усредненной мощности потока внешних частиц,
– доля вносимой в ракету усредненной мощности потока внешних частиц, 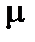 – доля усредненной мощности, передаваемая ракете непотенциальными силами в процессах с выделением джоулева тепла, трением и т.п.; в реальности параметр
– доля усредненной мощности, передаваемая ракете непотенциальными силами в процессах с выделением джоулева тепла, трением и т.п.; в реальности параметр 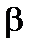 зависит от функции распределения внешних частиц, взаимодействующих с корпусом ракеты, а
зависит от функции распределения внешних частиц, взаимодействующих с корпусом ракеты, а 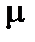 – от конкретных процессов в двигательных установках. Для простоты примем
– от конкретных процессов в двигательных установках. Для простоты примем 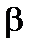 и
и 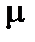 постоянными
постоянными
 ,
,  .
.
|
|
|
Это позволит сделать оценки релятивистских поправок к выражению для мощности. Раскладывая в ряд (2.6.3) по малым величинам 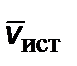 ,
, 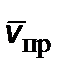 (скорость присоединения), имеем
(скорость присоединения), имеем
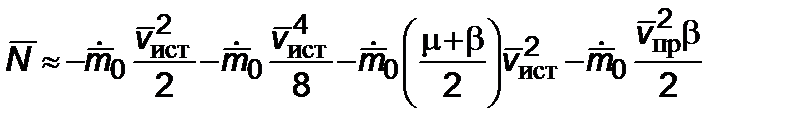 . (2.6.4)
. (2.6.4)
Тогда
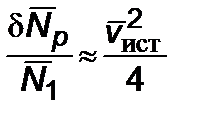 , (2.6.5)
, (2.6.5)
где 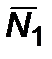 – нерелятивистское значение мощности. Рассмотрим случай
– нерелятивистское значение мощности. Рассмотрим случай 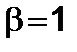 ,
, 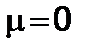 . Тогда
. Тогда
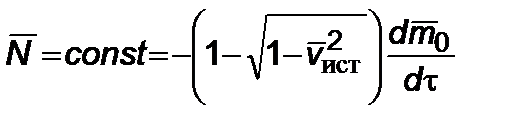 .
. 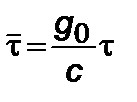 . (2.6.6)
. (2.6.6)
Интегрируя (2.6.6), имеем зависимость массы от бортового времени
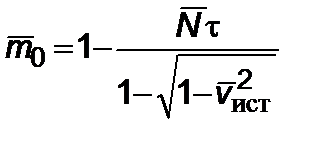 ,
, 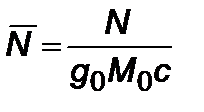 . (2.6.7)
. (2.6.7)
С другой стороны, согласно релятивистскому решению Аккарета для массы имеем
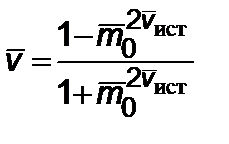 . (2.6.8)
. (2.6.8)
Обозначим, как в (2.5.6), выражение 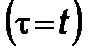
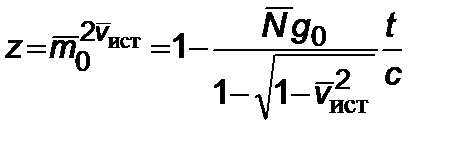 , (2.6.9)
, (2.6.9)
тогда по аналогии
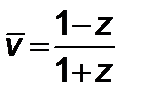 . (2.6.10)
. (2.6.10)
Раскладывая 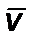 в ряд Тейлора, получим
в ряд Тейлора, получим
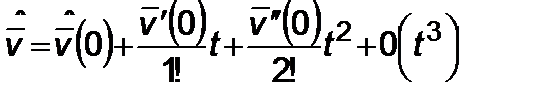 , (2.6.11)
, (2.6.11)
где 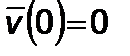 ;
;
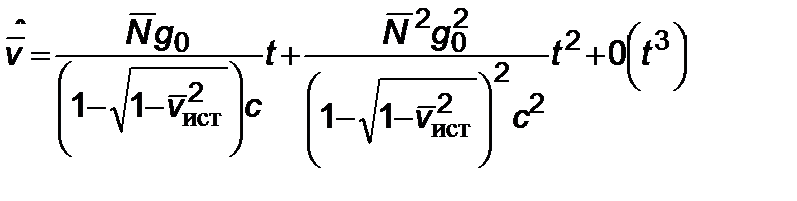 . (2.6.12)
. (2.6.12)
Учитывая, что 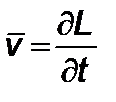 , получим выражение для дальности
, получим выражение для дальности
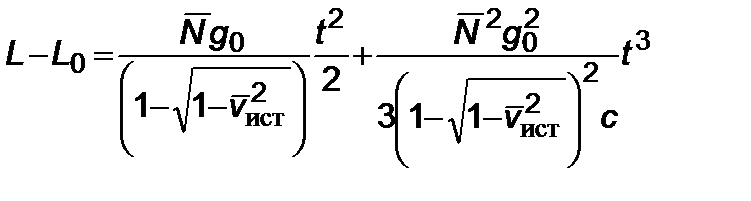 . (2.6.13)
. (2.6.13)
Для данного отрезка времени  поправка для дальности есть
поправка для дальности есть
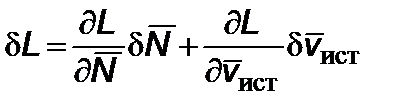 , (2.6.14)
, (2.6.14)
где
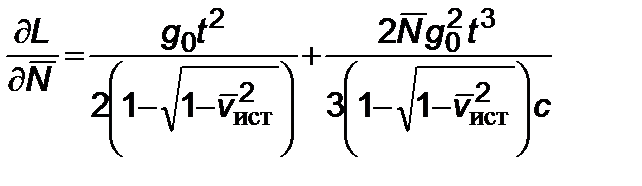 , (2.6.15)
, (2.6.15)
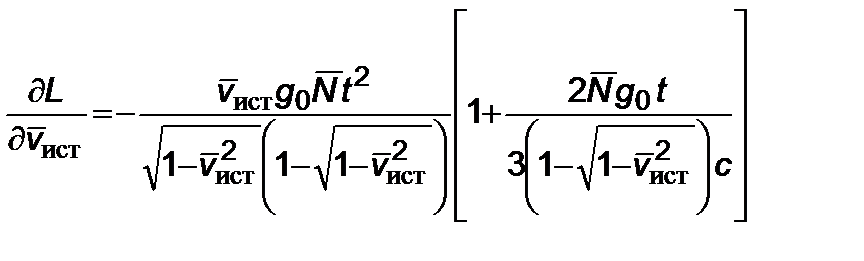 . (2.6.16)
. (2.6.16)
Таким образом, определена кинематика релятивистского движения с постоянной мощностью.
Дата добавления: 2019-01-14; просмотров: 217; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
