Формула Симпсона и ее погрешность
Как и в методе трапеций, для интегрирования функции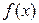 
в интервал интегрирования 
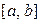разобьем на четное число n равных отрезков: 
, 
, …, 
. На каждых двух последовательных отрезках 
и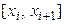 
подынтегральную функцию 
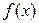заменим многочленом второй степени вида 
(рисунок 4).
Рассмотрим первые два отрезка , 
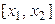. Через точки 
, 
и 
проведем параболу 
. Коэффициенты 
, 
, и 
уравнения этой параболы найдем из условий: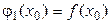 
, 
, 
, т.е.
(8)
Полагая, что 
, найдем
.
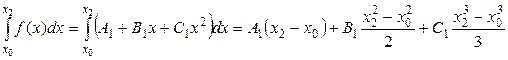После несложных преобразований с учетом условий (8) получим
. (9)
Теперь, используя точки 
, 
и 
графика функции 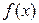на участке интегрирования 
, построим параболу 
. Принимая 
и подставив выражение для функции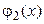 
, найдем
. (10)
Выполняя аналогичные операции для последующих точек графика функции 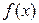, будем иметь:
(11)
Так как
,
то, учитывая (9)-(11), окончательно находим
или в компактном виде
, (12)
где 
; 
Полученная формула (12) называется формулой Симпсона или формулой парабол. Установлено [4], что погрешность этой формулы не превосходит величину
. (13)
На рисунке 5 приведена схема алгоритма вычисления определенного интеграла методом Симпсона. Основу алгоритма составляют блоки 5-8 вычисления суммы значений подынтегральной функции 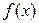на соответствующие коэффициенты 
.
|
|
|
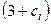Вычисление интеграла с автоматическим выбором
Шага интегрирования.
Анализ формул (6), (13)
; 
показывает, что для оценки точности вычисленных значений интеграла по формуле трапеций или Симпсона требуется определение производных второго или четвертого порядка подынтегральной функции. Во многих практических задачах вычисление этих производных весьма затруднительно. В этих случаях возникает проблема выбора шага h интегрирования (или числа n деления интервала 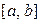), обеспечивающего вычисление интеграла с заданной точностью при малых затратах машинного времени. Эту проблему можно решить, применяя алгоритмы с автоматическим выбором величины шага h.
Сущность алгоритма с автоматическим выбором шага интегрирования заключается в двойном пересчете выбранным методом значений интеграла с шагами h и h/2. Полученные значения 
и 
сравнивают между собой. Если 
, то за значение интеграла, найденного с погрешностью 
, принимается значение . В противном случае производится дальнейшее деление шага пополам и вычисление новых приближений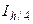 
, 
, …, пока не будет выполнено условие 
.
Первоначально, в качестве исходного значения шага h принимается 
для метода трапеций или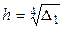 
для метода Симпсона.
|
|
|
Краткая справка о других видах формул вычисления интегралов. Формулы трапеций и Симпсона являются частными случаями общей формулы Ньютона-Котеса
, (14)
в которой коэффициенты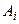 
определяются по формуле
, (15)
где
.
Так, полагая в формуле (14)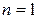 
, находим 
, 
и далее получим, что 
, т.е. формулу трапеций.
Для 
имеем 
; 
; 
. Учитывая, что 
, получим формулу Симпсона
.
Таким образом, посредством числа n можем задать любую степень многочлена, аппроксимирующего подынтегральную функцию вычисляемого интеграла.
Кроме формулы Ньютона-Котеса, для вычисления интеграла могут быть использованы формулы Чебышева, Гаусса и другие. Однако, при применении любой из формул численного определения интеграла следует учитывать характер изменения функции 
на интервале интегрирования 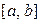. В частности, при наличии большого числа нулей подынтегральной функции или при большом числе ее экстремумов (рисунок 6) точность формул численного интегрирования существенно снижается. В таких случаях рекомендуется весь интервал 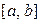разбить на частичные отрезки, внутри каждого из которых функция 
и ее производная сохраняют постоянный знак (если это возможно). далее производить вычисление интеграла частями, выбирая для каждого частичного отрезка, вообще говоря, свой шаг.
|
|
|
Контрольные вопросы по теме 8
1. Приведите в общем виде формулировку задачи вычисления интеграла. Что собой представляет формула Ньютона-Лейбница, и при каких условиях она позволяет найти значение интеграла 
? В каких случаях инженерной и научной практики возникает необходимость применения численных методов интегрирования функций?
2. Различают две группы приближенных методов вычисления интеграла: аналитические и численные. Поясните сущность методов этих групп. Что называют квадратурой и что – квадратурной формулой?
3. Что составляет основу численных методов вычисления интегралов, и какой общий подход используется в этих методах? По каким признакам различают методы численного интегрирования (прямоугольников, трапеций, Симпсона, Гаусса и др.)?
4. Поясните сущность метода прямоугольников и его разновидностей (левых, правых прямоугольников и средних). Какая из квадратурных формул метода прямоугольников позволяет получить значение интеграла с меньшей погрешностью при неизменном числе n элементарных отрезков интервала интегрирования (a, b)?
|
|
|
5. Поясните сущность метода трапеций. Приведите его простейшую квадратурную формулу и ее остаточный член с указанием наименований величин, входящих в формулы.
6. Как можно уменьшить погрешность результата вычисления интеграла методом трапеций? Какой вид при этом примет квадратурная формула трапеций?
7. Поясните сущность метода Симпсона. Приведите его квадратурную формулу и ее остаточный член с указанием наименований величин, входящих в формулы. В каком случае при вычислении интеграла методом Симпсона отсутствует погрешность метода решения интеграла?
8. Кроме погрешности метода, какие еще погрешности могут возникать при численном вычислении интегралов? Поясните причины, обуславливающие эти погрешности.
9. Приведите схему алгоритма вычисления интеграла с точностью Δ методом трапеций с автоматическим выбором шага интегрирования.
[1] Полагаем, что соответствующие производные функции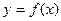 
существуют.
[2] См. Лекция 5 тема 6
Дата добавления: 2019-01-14; просмотров: 1077; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!