Приближенное дифференцирование с использованием
Лекция 6
2018/2019 уч. г.
Тема 7. Численное дифференцирование функций
Лк –1 ч., ПЗ – 2 ч., СРС – 10 ч.
1. Постановка задачи. Аппроксимация производных. Погрешность численного дифференцирования.
2. Приближенное дифференцирование с использованием интерполяционных формул.
3. Графическое дифференцирование функций.
Тема 8. Численное интегрирование функций
Лк –1 ч., ПЗ – 2 ч., СРС – 10 ч.
1. Постановка задачи численного интегрирования функций. Технологические задачи, содержащие задачу численного интегрирования.
2. Формула трапеций и ее погрешность.
3. Формула Симпсона и ее погрешость.
4. Вычисление интеграла с автоматическим выбором шага интегрирования.
Литература.
1. Данилина Н.И. и др. Вычислительная математика: Учеб. пособие для техникумов. – М.: Высш. шк., 1985, с.344-388.
2. Демидович Б.П. Основы вычислительной математики: Учеб. пособие для высш. техн. учеб. заведений. М.: ФИЗМАТЛИТ, 1960, с. 562-585, 588-593, 604-607, 618-621, 627-633.
3. Копченова Н.Н., Марон И.А. Вычислительная математика в примерах и задачах. Учеб. пособие. – СПб.: Изд-во «Лань», 2008, с.127-157, 168-174.
4. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2005, с.72-104.
5. Жидков Е.Н. Вычислительная математика: учебник для студ. Учреждений высш. проф. образования. – М.: Издательский центр «Академия», 2013, с.81-89, 93-98, 111-112.
Тема 7. Численное дифференцирование функций
|
|
|
1. Постановка задачи. Аппроксимация производных. Погрешность численного дифференцирования.
2. Приближенное дифференцирование с использованием интерполяционных формул.
3. Графическое дифференцирование функций.
Постановка задачи. Аппроксимация производных
При решении задач часто возникает необходимость вычисления производных заданных порядков от функции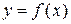 
. Вспомним, что производной функции 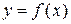называется предел отношения приращения функции Δy к приращению аргумента Δx при стремлении Δx к нулю
, 
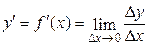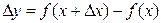. (1)
Обычно вычисление производных производят по известным в высшей математике формулам и правилам и к выражению (1) не обращаются. Однако при решении задач нередко функция 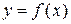задана таблицей своих значений y0, y1, y2 … в узлах x0, x1, x2 … или имеет сложное аналитическое выражение f(x). В этих случаях осуществляют приближенное дифференцирование, в частности, используя формулу (1). Значение шага Δx при этом полагают равным некоторому конечному числу и для вычисления производной получают формулу
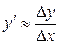. (2)
Это соотношение называется аппроксимацией (приближением) производной с помощью отношения конечных разностей (значения Δ y , Δ x в формуле (2) конечные в отличие от их бесконечно малых значений в (1)). В зависимости от способа вычисления конечных разностей можно получить различные формулы для вычисления производной в одной и той же точке. Рассмотрим их.
|
|
|
Постановка задачи. Пусть функция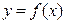 
задана таблицей своих значений y0, y1, y2 … в узлах x0, x1, x2 … Шаг Δx изменения аргумента постоянный и равен h. Необходимо вычислить производную 
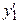функции 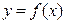в узле x = x1.
В зависимости от того как находится конечная разность Δy, производная 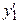может быть вычислена одной из трех формул:
с помощью левых разностей
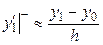; (3)
с помощью правых разностей
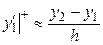; (4)
с помощью центральных разностей
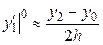. (5)
Можно найти также выражения для старших производных. Например,
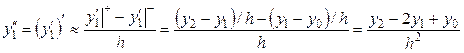. (6)
Аналогично можно найти производные третьего и более порядка.
Погрешность численного дифференцирования. Аппроксимируем функцию f(x) некоторой функцией φ(x), т. е. представим ее в виде
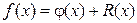, (7)
где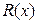 
- отклонение значения функции 
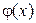от значения функции 
.
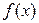В качестве аппроксимирующей функции φ(x) можно взять сумму первых членов некоторого ряда или интерполяционную функцию. Тогда погрешность аппроксимации R(x) определяется остаточным членом ряда или интерполяционной формулы.
|
|
|
Функция φ(x) может быть использована также для приближенного вычисления производной функции f(x). Дифференцируя выражение (7) необходимое число раз можно найти значения производных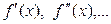 
:
, 
,…
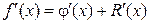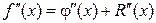В качестве приближенного значения производной порядка k функции f(x) можно принять значение соответствующей производной функции φ(x), т. е.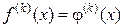 
. В этом случае величина
,
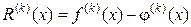характеризующая отклонение приближенного значения производной от ее истинного значения, называется погрешностью аппроксимации производной.
При численном дифференцировании функции, заданной в виде таблицы с шагом h, эта погрешность зависит от значения h, и ее записывают в виде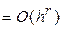 
(последнее читается как 
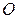большое от 
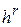; это означает, что 
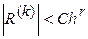, где C > 0). Показатель степени r называется порядком погрешности аппроксимации производной (или порядком точности данной аппроксимации). При этом предполагается, что значение шага h по модулю меньше единицы.
Оценку погрешности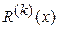 
можно найти с помощью ряда Тейлора
|
|
|
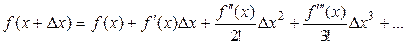
Пусть функция 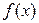задана в виде таблицы 
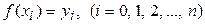. Запишем ряд Тейлора при 
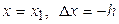с точностью до членов порядка h2:
.
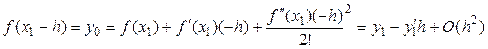Отсюда значение производной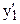 
в точке 
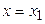равно:
.
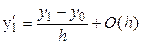Это выражение совпадает с формулой (3), которая, как видим, является аппроксимацией первого порядка (r = 1). Аналогично, записывая ряд Тейлора при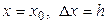 
, можно получить аппроксимацию (4). Она также будет иметь первый порядок.
Для оценки погрешностей аппроксимаций (5) и (6) запишем ряд Тейлора для точки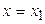 
, полагая 
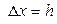и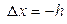 
. Соответственно получим:
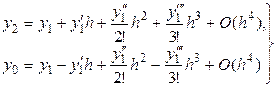, (8)
Вычитая эти равенства одно из другого, после преобразований получим
,
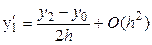т. е. аппроксимация производной с помощью центральных разностей имеет погрешность второго порядка.
Складывая равенства (8), находим оценку погрешности аппроксимации производной второго порядка вида (6)
.
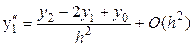Она имеет второй порядок. Аналогично можно найти оценку погрешностей производных третьего и более порядков.
Рассмотренная погрешность численного дифференцирования является остаточной погрешностью, так как она вызвана прерыванием процесса вычисления бесконечного ряда Тейлора на некотором его члене. Эту погрешность называют также погрешностью усечения, которая определяется величиной первого из отброшенных членов ряда.
Отметим, что остаточная погрешность уменьшается с уменьшением шага h только до некоторого предельного значения, после чего дальнейшее уменьшение h не повышает точность результатов численного дифференцирования.
Погрешности численного дифференцирования возникают также вследствие задания неточных значений функции 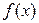в узлах 
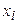и округления результатов промежуточных вычислений. При этом эти погрешности, как правило, возрастают с уменьшением шага h.
Приближенное дифференцирование с использованием
Интерполяционных формул
Пусть имеем функцию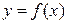 
заданную на отрезке [a, b] таблицей своих значений 
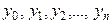в узлах 
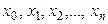. Шаг изменения аргумента x постоянный и равен h. Необходимо вычислить производную 
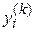функции 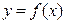в узле 
.
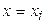Для нахождения производных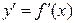 
, 
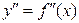[1] и т. д. функцию 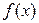аппроксимируем интерполяционным многочленом Ньютона
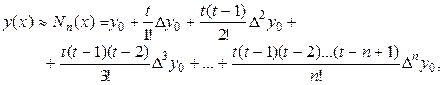(9)
где 
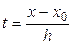и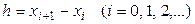 
.
Выполнив перемножение биномов, получим:
.
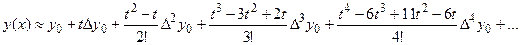Так как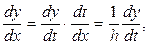 
то
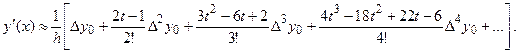(10)
Аналогично, так как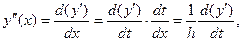 
то
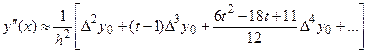. (11)
Таким же способом в случае необходимости можно вычислить производные функции 
любого порядка.
Пример. Вычислить в точке x = 0,1 первую и вторую производные функции, заданной в виде таблицы 1 своих значений.
Таблица 1
| x | y | Δ y | Δ 2 y | Δ 3 y | Δ 4 y | Δ 5 y |
| 0 | 1,2833 | 0,5274 | 0,0225 | 0,0247 | -0,0298 | 0,0400 |
| 0,1 | 1,8107 | 0,5499 | 0,0472 | -0,0051 | 0,0102 | |
| 0,2 | 2,3606 | 0,5971 | 0,0421 | 0,0051 | ||
| 0,3 | 2,9577 | 0,6392 | 0,0472 | |||
| 0,4 | 3,5969 | 0,6864 | ||||
| 0,5 | 4,2833 |
Согласно исходным данным h =0,1, t = (0,1-0)/0,1 = 1. Дополним исходные данные конечными разностями Δy, Δ2y, Δ3y, Δ4y, Δ5y, каждая последующая из которых получается путем вычитания в предыдущей колонке верхней строки из нижней. Используя формулы (10), (11), получим
.
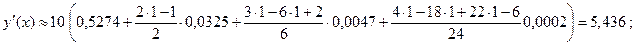
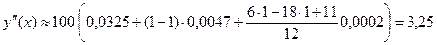Заметим, что при нахождении производных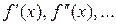 
в фиксированной точке x в качестве x0 следует выбирать ближайшее табличное значение аргумента. Число слагаемых в формулах вычисления производных зависит от количества узлов 
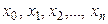, в которых используются значения y0, y1, y2 …, yn функции ). Как и при вычислении многочлена Ньютона, добавление нового узла означает добавление в формуле вычисления производной одного слагаемого.
Использование интерполяционных многочленов Ньютона для вычисления производных обуславливает необходимость определения конечных разностей Δk y (k = 1, 2, …). Однако на практике удобнее вычислять производные не через разности, а непосредственно через значения функции в узлах. Это позволяет выполнить применение интерполяционного многочлена Лагранжа с равномерным расположением узлов (xi - xi-1 = h = const, i = 1, 2, …, n).
Запишем интерполяционный многочлен Лагранжа L(x) и его остаточный член RL(x) для случая трех узлов интерполяции (n = 2)[2]
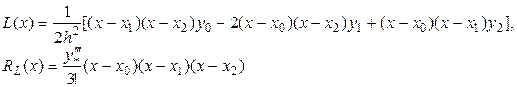
и найдем производные:
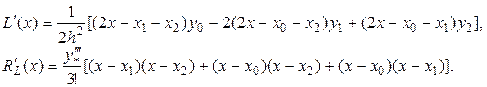
В приведенных формулах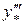 
значение производной третьего порядка в некоторой внутренней точке 
.
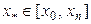Запишем выражение для производно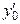й 
при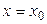 
:
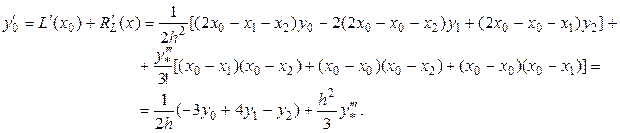
Аналогичные соотношения можно получить и для производных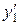 
и 
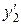при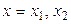 
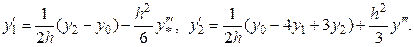
Для каждой из этих формул значения 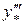, вообще говоря, различны. Используя интерполяционный многочлен Лагранжа и его остаточный член для случая четырех узлов (n = 3), получим следующие аппроксимации производных:
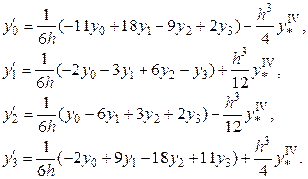
Так же можем получить формулы для производных для пяти и т. д. узлов. При этом, используя значения функции в n + 1 узле, получаем аппроксимацию производных n-го порядка точности. Эти формулы можно использовать не только для узлов x0, x1, x2 …, но и для любых узлов x = xi, xi+1,…, соответствующим образом изменяя значения индексов.
С помощью интерполяционных многочленов Лагранжа можно получить аппроксимации для старших производных.
В случае трех узлов интерполяции (n = 2) имеем
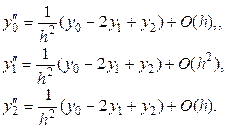
В случае четырех узлов интерполяции (n = 3) имеем
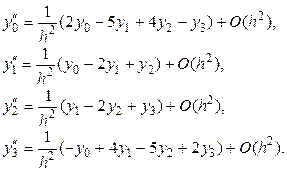
Следует заметить, что вычисление производных функции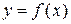 
может быть осуществлено также с применением интерполяционных многочленов Стирлинга и Бесселя, а также методом неопределенных коэффициентов [2, 4].
Дата добавления: 2019-01-14; просмотров: 1067; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!