Тема 8. Численное интегрирование функций
Лк –1 ч., ПЗ – 2 ч., СРС – 10 ч.
1. Постановка задачи численного интегрирования функций.
2. Формула трапеций и ее погрешность.
3. Формула Симпсона и ее погрешность.
4. Вычисление интеграла с автоматическим выбором шага интегрирования.
1. Постановка задачи численного интегрирования функций
В общем случае задача вычисления определенного интеграла формулируется следующим образом: необходимо вычислить интеграл вида
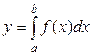(1)
на отрезке интегрирования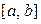 
.
Из курса математического анализа известно, что если подынтегральная функция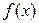 
непрерывна на отрезке 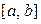и известна ее первообразная 
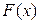, то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона - Лейбница
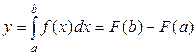. (2)
Напомним, что функция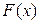 
в интервале 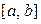называется первообразной для функции 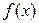, если во всем этом интервале 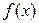является производной для функции 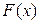, т.е.
.
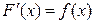Во многих инженерных задачах первообразную 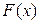не удается выразить через элементарные функции или она имеет сложный вид, неудобный для практического применения. Кроме того, в ряде задач не известна и сама подынтегральная функция 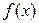, а заданы ее значения на интервале 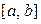, полученные, например, в результате экспериментальных исследований. В этом случае само понятие первообразной функции теряет смысл. В таких задачах возникает необходимость в приближенных метода вычисления определенного интеграла. Различают аналитические и численные методы приближенного вычисления интеграла.
|
|
|
Аналитические методы заключаются в приближенном построении первообразной и последующем применении формулы Ньютона-Лейбница. Численные методы позволяют непосредственно, не используя формулу (2), найти числовое значение интеграла по заданным или вычисляемым значениям подынтегральной функции в точках интервала интегрирования.
В данной работе рассматриваются только численные методы интегрирования функций. Процесс численного определения значения однократного интеграла называется квадратурой, а соответствующие формулы - квадратурными формулами.
Основу численных методов составляет геометрический смысл определенного интеграла, согласно которому интеграл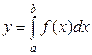 
представляет собой площадь криволинейной трапеции aABb (рисунок 1).
Общая идея всех численные методов заключается в том, что подынтегральную функцию 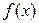на отрезке интегрирования 
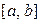заменяют некоторой другой функцией 
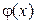, обычно интерполяционным многочленом, для которого интеграл 
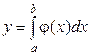может быть вычислен. Затем полагают, что 
.
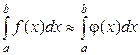В зависимости от вида выбранной функции 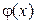и способа подбора точек (узлов) x0, x1, x2,…, xn, в интервале 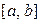различают следующие методы численного интегрирования: прямоугольников, трапеций, Симпсона (парабол), Гаусса и др. Наиболее часто при решении инженерных задач используются методы трапеций и Симпсона.
|
|
|
2. Формула трапеций и ее погрешность
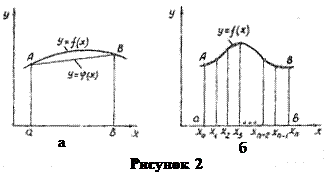
В этом методе подынтегральная функция 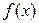заменяется многочленом первой степени 
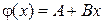(рисунок 2, а), коэффициенты A и B которого определяются из условий:
; 
.
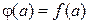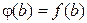Приближенно полагая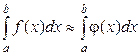 
, находим
.
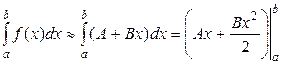Учитывая, что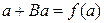 
и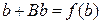 
, получим
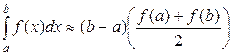. (3)
Установлено, что остаточный член (погрешность) полученной квадратурной формулы (3) составляет
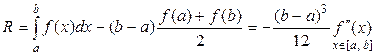. (4)
Отсюда следует, что если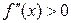 
, то формула трапеций дает значение интеграла с избытком, если же 
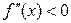, то с недостатком. Данная погрешность отражает различие между точным значением интеграла и его приближенным значением, найденным по формуле трапеции, т.е. является погрешностью метода решения.
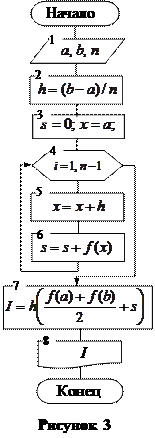Для уменьшения погрешности вычисления интеграла интервал интегрирования 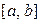разбивают на n равных отрезков: 
, 
, …, 
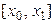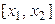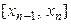. На каждом отрезке 
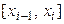подынтегральная функция 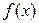заменяется линейным многочленом вида 
, т.е. график функции 
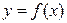аппроксимируется ломаной линией (рисунок 2, б), соединяющей точки 
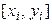. Применяя формулу трапеций для вычисления интеграла на каждом элементарном отрезке интегрирования, получим
|
|
|
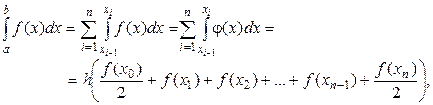
где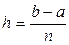 
.
Учитывая, что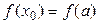 
и 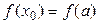, окончательно находим
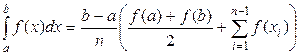. (5)
Полученная формула (5) называется общей формулой трапеций, которую и применяют для вычисления определенного интеграла. Блок-схема алгоритма вычисления интеграла по формуле (5) приведена на рисунке 3.
В ней блоками 4-7 отображен циклический процесс вычисления суммы s значений подынтегральной функции 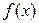в узлах 
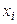интервала интегрирования 
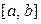. Окончательное вычисление значения интеграла представлено блоком 7.
Используя формулу (4) нетрудно убедиться, что остаточный член общей формулы трапеций составляет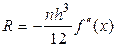 
, где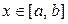 
. Таким образом, погрешность вычисления определенного интеграла по формуле (5) не превосходит величины
| (начало) [оА* |
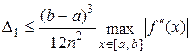, (6)
которая является погрешностью метода вычисления интеграла.
Однако, наряду с погрешностью метода вычисления интеграла могут иметь место и погрешности, обусловленные такими причинами, как:
· наличие в выражении 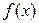подынтегральной функции различных физических констант или значения 
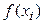функции 
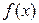являются результатами экспериментальных исследований (погрешность исходной информации);
|
|
|
· прерывание бесконечного вычислительного процесса получения значений подынтегральной функции (остаточная погрешность);
· округление результатов промежуточных и окончательных вычислений значений подынтегральной функции (погрешность округления)
Эти погрешности, связанные с выполнением действий над приближенными числами, являются вычислительной погрешностью и в определенной степени переносятся в результат вычислений значений интеграла. Установлено, если значения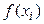 
в узлах интегрирования получены с одинаковой абсолютной погрешностью ε, то суммарная вычислительная погрешность 
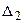составляет 
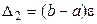. Следовательно, общая предельная погрешность вычисления определенного интеграла по формуле трапеций составит
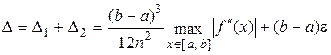. (7)
Дата добавления: 2019-01-14; просмотров: 225; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!