Билет №6. Двоичная логика. Основные операции.
Двоичная логика
1 – правда
0 – ложь
Основные логические операции
- отрицание
∧ - конъюнкция («и» логическое умножение)
\/ - дизъюнкция («или» логическое сложение)
Аксиомы: 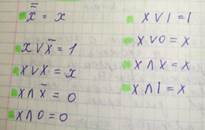
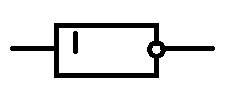 Таблица истинности и обозначения:
Таблица истинности и обозначения:
Отрицание:
| X | |
| 0 | 1 |
| 1 | 0 |
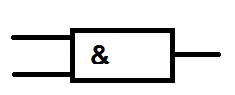 Конъюнкция «И» (умножение)
Конъюнкция «И» (умножение)
| A | B | A ∧ B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
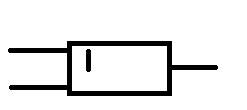 Дизъюнкция «ИЛИ» (сложение)
Дизъюнкция «ИЛИ» (сложение)
| A | B | A V B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Билет №7. Дополнительные операции.
· Эквиваленция (исключающее или-не) «↔» (( A v B ) /\ ( v ))
| A | B | A ↔ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
· Импликация (следование) «→» ( V B )
| A | B | A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
· сложение по модулю 2 (искл. ИЛИ) « 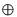 » (( A /\ ) v ( /\ B ))
» (( A /\ ) v ( /\ B ))
| A | B | A 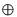 B B
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
· штрих Шеффера «|» ()
| A | B | A | B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
· стрелка Пирса «↓» ()
| A | B | A ↓ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Законы де Моргана:
· = ∧
· =v
Билет №8. Двоичная логика. Базисы. Переход от канонического базиса к базисам «И-НЕ» и «ИЛИ-НЕ».
Базисы
· И-ИЛИ-НЕ (, V, ∧ )
· И-НЕ (, ∧)
· ИЛИ-НЕ (, V )
· |
· ↓
Штрих Шеффера. Построение базиса.
· = a | a
· a ∧ b = = (a | b) | (a | b)
· a V b = = =
Стрелка Пирса. Построение базиса
· = a ↓ a
· a V b = (a ↓ b) ↓ (a ↓ b)
· a ∧ b = ((a ↓ a) ↓ (b ↓ b) ↓ (a ↓ a) ↓ (b ↓ b))
Билет №9. Троичная логика. Основные операции.
Один из видов многозначной логики, использующий три значения. Если параметр неизвестен, можно получить только 1 или .
1 – истина
0 – неизвестно
– ложь
Логическое умножение Логическое сложение
| a | b | a ∧ b | a | b | a V b | перенос | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | ||||
| 1 | 1 | 0 | 0 | |||||
| 1 | 1 | 0 | 0 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 | |||
| 1 | 1 |
Логическое отрицание
| a | |
| 0 | 0 |
| 1 | |
| 1 |
Билет №10. Мультиплексор. Назначение. УГО. Схема реализации.
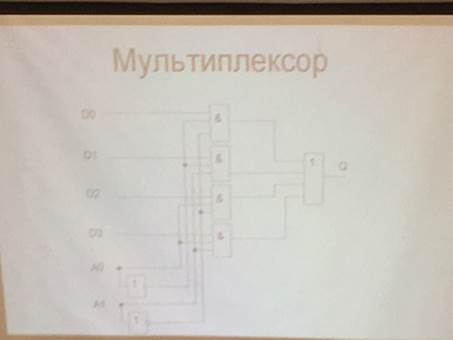
Мультиплексор
Устройство (управляемый переключатель), которое в зависимости от управляющих сигналов подаёт значение одного из информационных входов на единственный выход.
Обладает 2N информационными входами, N управляющими входами, одним (необязательным) разрешающим входом и одним выходом.
Назначение
передача сигнала из нескольких входов на один выход, причем выбор заказанного выхода осуществляется при помощи сочетания определенных управляющих сигналов.
· «ленивая» реализация логических функций, когда минимизацией функций можно пренебречь (но приводит к доп. затратам)
· В качестве коммутатора N к 1 ( преобразование параллельного кода в последовательный, для поочерёдного подключения многих источников информации к одному потребителю )
УГО (условное графическое обозначение)
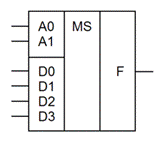 Количество информационных входов = 2управляющих входов
Количество информационных входов = 2управляющих входов
Схема реализации.
Билет №11. Демультиплексор. Назначение. УГО. Схема реализации.
Демультиплексор
Устройство, которое в зависимости от управляющих сигналов передаёт значение входных сигналов на один из выходов.
Назначение
Управляемая передача данных от одного источника информации в несколько информационных каналов.
УГО
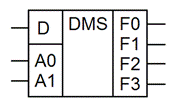 Количество выходов = 2количество управляющих входов
Количество выходов = 2количество управляющих входов
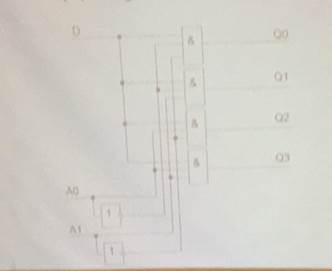
Схема реализации
Билет №12. Сумматор. Назначение. УГО. Схема реализации полного одноразрядного сумматора.
Сумматор, УГО
Устройство, которое выдаёт на выходе арифметическую сумму значений на входе.
Единица переноса
P-единиц переноса для старшего каскада
УГО
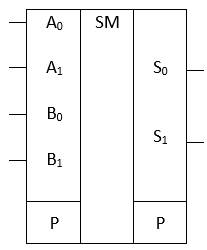 A0 – AN – первое слагаемое
A0 – AN – первое слагаемое
B0 – BN – второе слагаемое
S0 – SM – сумма
Сумматор
| Pi-1 | Ai | Bi | Si | Pi |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Назначение
Предназначен для нахождения арифметической суммы кодов поданных значений.
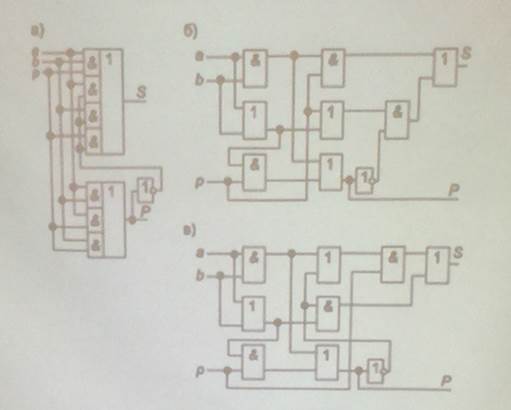
Схема реализации полного одноразрядного сумматора
Билет №13. Сумматор. Назначение. УГО. Схема реализации полного одноразрядного сумматора на полусумматорах.
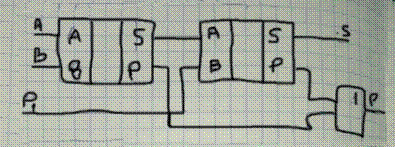
Дополнение к сумматорам
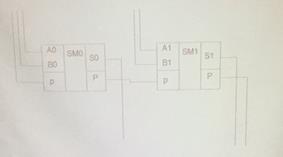 Сумматор (каскады). Двухразрядный на основе одноразрядных.
Сумматор (каскады). Двухразрядный на основе одноразрядных.
Основная проблема каскадирования сумматоров – необходимость вычисления переноса от суммы предыдущих разрядов для вычисления суммы и переноса текущего разряда. => Такой каскадный сумматор работает очень долго. Для ускорения используется построение схем многоразрядных сумматоров на основе логических элементов; использование схем быстрого переноса.
Дата добавления: 2019-01-14; просмотров: 2194; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
