Модуль 3. РАСТЯЖЕНИЕ И СЖАТИЕ
Общие понятия. Продольные силы. Эпюры
Анализируя окружающую нас действительность, мы замечаем, что рыболовная леска, как и канат лифта растянуты. Стены зданий, промышленные трубы сжаты нагрузкой, обусловленной их собственным весом. Это самые простые и очевидные виды деформаций растяжения и сжатия.
Изучая деформации растяжения и сжатия, будем рассматривать такие загружения стержней, при которых равнодействующие всех сил и реакций лежат на одно прямой, совпадающей с продольной осью элемента (рис. 3.1).
В этом случае в поперечном сечении элемента возникает один внутренний силовой фактор – продольное усилие N (продольная сила). 
Для определения внутренних усилий (продольных сил) используется метод сечений, который заключается в следующем (рис. 3.2).
Алгоритм метода сечений:
1. Мысленно рассекаем стержень плоскостью, перпендикулярной продольной оси стержня на две части;
2. Рассматриваем в равновесии одну из частей: верхнюю или нижнюю, правую или левую (в данном случае нижнюю);
3. Неизвестное усилие N, возникающее в сечении, считаем положительным и направляем в сторону от сечения (в сторону отброшенной части);
4. Записываем уравнение равновесия для рассматриваемой части элемента:
ΣFz = 0 N – P = 0 или N = P
5. Полученный в результате решения знак «+» свидетельствует о том, что усилие растягивающее, знак минус – сжимающее.
Следовательно, метод сечений – алгоритм последовательных действий, с помощью которых определяют внутренние усилия.
|
|
|
Пример 3.1. Определить внутренние усилия на отдельных участках элемента, загруженного, как показано на рис. 3.3. Построить эпюру продольных усилий.
 |
| ΣF2 = 0 N1 = P1 = 5 кН | |||
| ΣF2 = 0 N2 = P1 – P3 = 2 кН | ||||
| ΣF2 = 0 N3 = -P4 = -7 кН |
Стержень имеет три участка. Пользуясь приведенным выше алгоритмом, определяем усилия на каждом участке. По результатам найденных значений N строим эпюру продольных усилий.
Эпюра – график, показывающий изменение какой-либо величины (усилия, напряжения, деформации и т. д.) по длине элемента или по высоте (ширине) поперечного сечения.
Эпюра продольных усилий – график, показывающий величину продольного усилия в каждом сечении по длине элемента. Ордината эпюры в определенном масштабе равна численному значению продольного усилия в рассматриваемом сечении элемента.
Положительные значения продольных усилий откладываем вверх от оси, отрицательные – вниз в определенном масштабе или, как правило, соразмерно значениям величин усилий.
Напряжения и деформации при растяжении. Закон Гука
|
|
|
Рассмотрим призматический стержень с постоянной площадью поперечного сечения F, к концам которого приложена распределенная нагрузка, равнодействующая которой равна P (рис. 3.4).
На элементарную площадку dF действует элементарное усилие dN.
Отсюда dN = σ dF или N = 
σ dF (3.1)
В формуле (3.1) неизвестен закон распределения нормальных напряжений по площади поперечного сечения. Для ответа на этот вопрос на боковую поверхность элемента нанесем систему линий, перпендикулярных продольной оси элемента. После приложения нагрузки отмечаем, что эти линии не деформируются, а перемещаются поступательно. Это возможно в том случае, когда напряжения s по площади поперечного сечения распределены равномерно. Это предположение впервые высказал голландский ученый Д. Бернулли.
Гипотеза Бернулли – сечения плоские до деформации, остаются плоскими и после деформации.
Следовательно, формула (3.1) может быть записана как:
N = σ 
dF = σF
Отсюда найдем s = 
(3.2)
Для определения деформаций рассмотрим призматический стержень длиной l с размерами поперечного сечения a и b. После приложения нагрузки стержень удлинился и длина его стала равной l1, а размеры поперечного сечения уменьшились и стали равными a1 и b1 (рис. 3.5).
|
|
|
 |
На расстоянии z выделим участок стержня длиной dz. После приложения нагрузки его длина станет равной dz + Δdz.
Согласно определению относительная деформация
= 
, или Δ dz = ε dz
С учетом гипотезы Бернулли, если σ = const, следовательно, и ε = const, получим:
Δl = Δε dz = ε 
dz = εl
Продольная деформация при простом растяжении равна
= 
(3.3)
Здесь Δl - абсолютная продольная деформация.
Рассуждая аналогично найдем поперечные деформации, которые берутся со знаком «-», так как сечение сужается.
= - 
; 
= - 
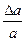Величины - Δa и Δb - абсолютная поперечная деформация.
Для изотропных материалов
| | = | 
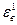| = ε1
Французский ученый Пуассон установил, что отношение
| 
| = μ есть величина постоянная. (3.4)
Как будет показано ниже, коэффициент Пуассона μ меняется в пределах
|
|
|
0≤ μ ≤0,5 (3.5)
На основании гипотезы о линейной зависимости между напряжениями и деформациями (1.18) можно записать
σ = εE (3.6)
σ = εE = E или 
= E, отсюда
(3.7)
Формула (3.7) - закон Гука для абсолютной деформации элемента.
EF - жесткость стержня при растяжении.
Принцип Сен-Венана
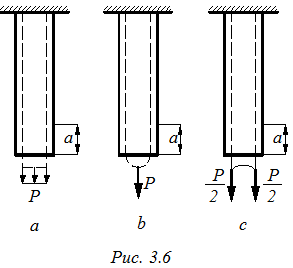Формулы (3.2) и (3.7) получены для случая растяжения стержня распределенной нагрузкой, приложенной к его торцам. В том случае, когда нагрузка прикладывается другим способом (рис. 3.6 а, в, с), гипотеза Бернулли наблюдается только в тех сечениях, которые удалены от места приложения ее на расстояние а, превышающее 1,5-2 раза больший его поперечный размер.
В этом случае напряжения у мест приложения нагрузки распределены не равномерно, о чем свидетельствуют деформации у мест приложения нагрузки. Это явление по имени французского ученого называется принципом Сен-Венана.
Принцип Сен-Венана - при нагружении элемента статически эквивалентной нагрузкой, у которой главный вектор и главный момент одинаковы, в сечениях, достаточно удаленных от мест приложения нагрузки, напряжения мало зависят от способа приложения нагрузки.
Дата добавления: 2018-11-24; просмотров: 273; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!