Понятие о напряжениях и деформациях в точке
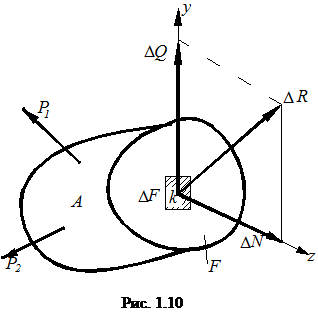На основании гипотезы о сплошности материала внутренние силы распределены по всему сечению. Выделим в произвольной точке k элемента А малую площадку ΔF. На нее действует равнодействующая внутренних сил ΔR (рис. 1.10)
Отношение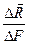 
= pcp - среднее напряжение в точке К
Предел отношения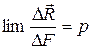 
- напряжение в точке k.
Разложив Δ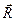 
на составляющие Δ 
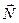и Δ 
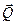получим:
lim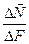 
= σ нормальное напряжение в точке k.
lim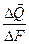 
= τ касательное напряжение в точке k
Следовательно, напряжение представляет собой силу, отнесенную к единице площади поперечного сечения.
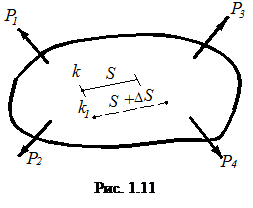Для определения деформаций в точке k рассмотрим отрезок S, исходящий из этой точки (рис. 1.11). В результате деформации точка k сместится в положение k1, а отрезок станет равным S1.
- ΔS = S1 - S называется абсолютной деформацией/
ε =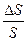 
относительная деформация в точке k.
МОДУЛЬ 2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ БРУСА
Сопротивление материалов – экспериментально теоретическая дисциплина, изучающая методы расчета элементов конструкций на прочность, жесткость и устойчивость. Вполне, понятно, что все эти качества элемента конструкции зависят не только от свойств материала, из которого выполнен элемент конструкции, но и от геометрических характеристик поперечных сечений. В качестве элемента конструкции сопротивление материалов рассматривает, как правило, брус, у которого два размера в 8-12 раз меньше третьего. Первые из них – это размеры поперечного сечения, от которых зависят его геометрические характеристики. Рассмотрим основные геометрические характеристики плоских сечений бруса.
|
|
|
Статические моменты площади. Центр тяжести сечения
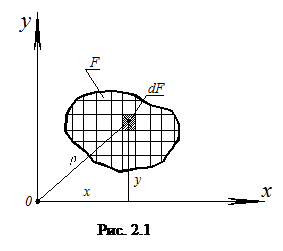Рассмотрим плоское сечение произвольной формы, связанное с прямоугольной декартовой системой координат х0у (рис. 2.1). Разобьём его на элементарные площадки линиями параллельными осям координат. Рассмотрим одну из таких площадок размером dFс координатами её центра тяжести х и у. Самой простой геометрической характеристикой сечения является его площадь F, определяемая интегралом:
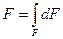(2.1)
где dF –дифференциал площади поперечного сечения бруса (рис. 2.1).
Интегралы вида
= 
, 
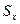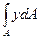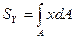(2.2)
называются статическими моментами площади сечения относительно осей x, y, соответственно.
При этом Sx и Sy могут быть положительными, отрицательными и равными нулю. Оси, относительно которых статические моменты площад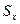и и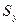 
равны нулю, называются центральными осями.
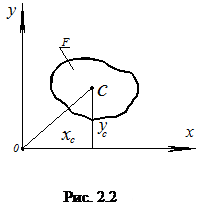
На основании теоремы о среднем (рис. 2.2) определенного интеграла формулы (2.2) можно записать так:
|
|
|
; 
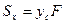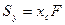(2.3)
Отсюда, координаты центра тяжести сечения.
, 
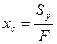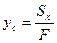(2.4)
Для сечения, составленного из простейших фигур с площадями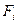 
, координаты центра тяжести определяются по формулам:
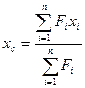
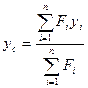(2.4*)
Здесь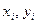 
координаты центров тяжестей каждой составляющей фигуры в системе предварительно выбранных вспомогательных осей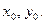 
Пример 2.1.
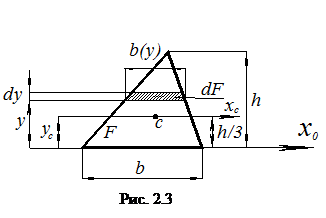Определим координату центра тяжести треугольника с высотой h, основанием b (рис. 2.3).
Для решения задачи воспользуемся формулами (2.4). Выберем случайную ось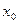 
. Статический момент площади относительно вспомогательной оси 
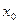найдем непосредственным интегрированием выражения:
= 
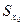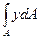(а)
На расстоянии у от этой оси выделим элементарную площадку dF высотой dy. Тогда дифференциал площади
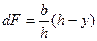
Статический момент площади относительно вспомогательной оси 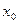(а)
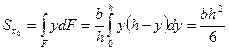
Координата центра тяжести треугольника
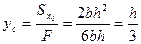
Следовательно, центр тяжести треугольника находится на расстоянии треть высоты от его основания.
Дата добавления: 2018-11-24; просмотров: 479; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!